DecisionTreeRegressor#
- class sklearn.tree.DecisionTreeRegressor(*, criterion='squared_error', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, ccp_alpha=0.0, monotonic_cst=None)[source]#
A decision tree regressor.
Read more in the User Guide.
- Parameters:
- criterion{“squared_error”, “friedman_mse”, “absolute_error”, “poisson”}, default=”squared_error”
The function to measure the quality of a split. Supported criteria are “squared_error” for the mean squared error, which is equal to variance reduction as feature selection criterion and minimizes the L2 loss using the mean of each terminal node, “friedman_mse”, which uses mean squared error with Friedman’s improvement score for potential splits, “absolute_error” for the mean absolute error, which minimizes the L1 loss using the median of each terminal node, and “poisson” which uses reduction in the half mean Poisson deviance to find splits.
Added in version 0.18: Mean Absolute Error (MAE) criterion.
Added in version 0.24: Poisson deviance criterion.
- splitter{“best”, “random”}, default=”best”
The strategy used to choose the split at each node. Supported strategies are “best” to choose the best split and “random” to choose the best random split.
- max_depthint, default=None
The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min_samples_split samples.
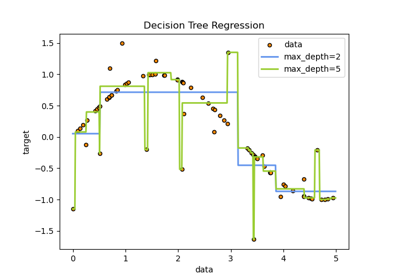
For an example of how
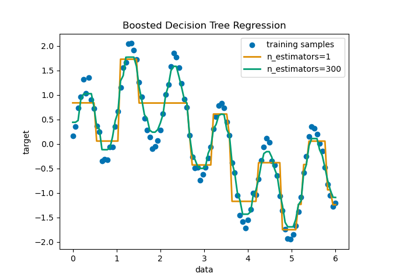
max_depthinfluences the model, see Decision Tree Regression.- min_samples_splitint or float, default=2
The minimum number of samples required to split an internal node:
If int, then consider
min_samples_splitas the minimum number.If float, then
min_samples_splitis a fraction andceil(min_samples_split * n_samples)are the minimum number of samples for each split.
Changed in version 0.18: Added float values for fractions.
- min_samples_leafint or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least
min_samples_leaftraining samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.If int, then consider
min_samples_leafas the minimum number.If float, then
min_samples_leafis a fraction andceil(min_samples_leaf * n_samples)are the minimum number of samples for each node.
Changed in version 0.18: Added float values for fractions.
- min_weight_fraction_leaffloat, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample_weight is not provided.
- max_featuresint, float or {“sqrt”, “log2”}, default=None
The number of features to consider when looking for the best split:
If int, then consider
max_featuresfeatures at each split.If float, then
max_featuresis a fraction andmax(1, int(max_features * n_features_in_))features are considered at each split.If “sqrt”, then
max_features=sqrt(n_features).If “log2”, then
max_features=log2(n_features).If None, then
max_features=n_features.
Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than
max_featuresfeatures.- random_stateint, RandomState instance or None, default=None
Controls the randomness of the estimator. The features are always randomly permuted at each split, even if
splitteris set to"best". Whenmax_features < n_features, the algorithm will selectmax_featuresat random at each split before finding the best split among them. But the best found split may vary across different runs, even ifmax_features=n_features. That is the case, if the improvement of the criterion is identical for several splits and one split has to be selected at random. To obtain a deterministic behaviour during fitting,random_statehas to be fixed to an integer. See Glossary for details.- max_leaf_nodesint, default=None
Grow a tree with
max_leaf_nodesin best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.- min_impurity_decreasefloat, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.
The weighted impurity decrease equation is the following:
N_t / N * (impurity - N_t_R / N_t * right_impurity - N_t_L / N_t * left_impurity)
where
Nis the total number of samples,N_tis the number of samples at the current node,N_t_Lis the number of samples in the left child, andN_t_Ris the number of samples in the right child.N,N_t,N_t_RandN_t_Lall refer to the weighted sum, ifsample_weightis passed.Added in version 0.19.
- ccp_alphanon-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than
ccp_alphawill be chosen. By default, no pruning is performed. See Minimal Cost-Complexity Pruning for details. See Post pruning decision trees with cost complexity pruning for an example of such pruning.Added in version 0.22.
- monotonic_cstarray-like of int of shape (n_features), default=None
- Indicates the monotonicity constraint to enforce on each feature.
1: monotonic increase
0: no constraint
-1: monotonic decrease
If monotonic_cst is None, no constraints are applied.
- Monotonicity constraints are not supported for:
multioutput regressions (i.e. when
n_outputs_ > 1),regressions trained on data with missing values.
Read more in the User Guide.
Added in version 1.4.
- Attributes:
feature_importances_ndarray of shape (n_features,)Return the feature importances.
- max_features_int
The inferred value of max_features.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
- n_outputs_int
The number of outputs when
fitis performed.- tree_Tree instance
The underlying Tree object. Please refer to
help(sklearn.tree._tree.Tree)for attributes of Tree object and Understanding the decision tree structure for basic usage of these attributes.
See also
DecisionTreeClassifierA decision tree classifier.
Notes
The default values for the parameters controlling the size of the trees (e.g.
max_depth,min_samples_leaf, etc.) lead to fully grown and unpruned trees which can potentially be very large on some data sets. To reduce memory consumption, the complexity and size of the trees should be controlled by setting those parameter values.References
[2]L. Breiman, J. Friedman, R. Olshen, and C. Stone, “Classification and Regression Trees”, Wadsworth, Belmont, CA, 1984.
[3]T. Hastie, R. Tibshirani and J. Friedman. “Elements of Statistical Learning”, Springer, 2009.
[4]L. Breiman, and A. Cutler, “Random Forests”, https://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm
Examples
>>> from sklearn.datasets import load_diabetes >>> from sklearn.model_selection import cross_val_score >>> from sklearn.tree import DecisionTreeRegressor >>> X, y = load_diabetes(return_X_y=True) >>> regressor = DecisionTreeRegressor(random_state=0) >>> cross_val_score(regressor, X, y, cv=10) ... ... array([-0.39, -0.46, 0.02, 0.06, -0.50, 0.16, 0.11, -0.73, -0.30, -0.00])
- apply(X, check_input=True)[source]#
Return the index of the leaf that each sample is predicted as.
Added in version 0.17.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.- check_inputbool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you’re doing.
- Returns:
- X_leavesarray-like of shape (n_samples,)
For each datapoint x in X, return the index of the leaf x ends up in. Leaves are numbered within
[0; self.tree_.node_count), possibly with gaps in the numbering.
- cost_complexity_pruning_path(X, y, sample_weight=None)[source]#
Compute the pruning path during Minimal Cost-Complexity Pruning.
See Minimal Cost-Complexity Pruning for details on the pruning process.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The training input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsc_matrix.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
The target values (class labels) as integers or strings.
- sample_weightarray-like of shape (n_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. Splits are also ignored if they would result in any single class carrying a negative weight in either child node.
- Returns:
- ccp_path
Bunch Dictionary-like object, with the following attributes.
- ccp_alphasndarray
Effective alphas of subtree during pruning.
- impuritiesndarray
Sum of the impurities of the subtree leaves for the corresponding alpha value in
ccp_alphas.
- ccp_path
- decision_path(X, check_input=True)[source]#
Return the decision path in the tree.
Added in version 0.18.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.- check_inputbool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you’re doing.
- Returns:
- indicatorsparse matrix of shape (n_samples, n_nodes)
Return a node indicator CSR matrix where non zero elements indicates that the samples goes through the nodes.
- fit(X, y, sample_weight=None, check_input=True)[source]#
Build a decision tree regressor from the training set (X, y).
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The training input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsc_matrix.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
The target values (real numbers). Use
dtype=np.float64andorder='C'for maximum efficiency.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node.
- check_inputbool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you’re doing.
- Returns:
- selfDecisionTreeRegressor
Fitted estimator.
- get_depth()[source]#
Return the depth of the decision tree.
The depth of a tree is the maximum distance between the root and any leaf.
- Returns:
- self.tree_.max_depthint
The maximum depth of the tree.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_n_leaves()[source]#
Return the number of leaves of the decision tree.
- Returns:
- self.tree_.n_leavesint
Number of leaves.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- predict(X, check_input=True)[source]#
Predict class or regression value for X.
For a classification model, the predicted class for each sample in X is returned. For a regression model, the predicted value based on X is returned.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.- check_inputbool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you’re doing.
- Returns:
- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
The predicted classes, or the predict values.
- score(X, y, sample_weight=None)[source]#
Return coefficient of determination on test data.
The coefficient of determination, \(R^2\), is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares
((y_true - y_pred)** 2).sum()and \(v\) is the total sum of squares((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value ofy, disregarding the input features, would get a \(R^2\) score of 0.0.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape
(n_samples, n_samples_fitted), wheren_samples_fittedis the number of samples used in the fitting for the estimator.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True values for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
\(R^2\) of
self.predict(X)w.r.t.y.
Notes
The \(R^2\) score used when calling
scoreon a regressor usesmultioutput='uniform_average'from version 0.23 to keep consistent with default value ofr2_score. This influences thescoremethod of all the multioutput regressors (except forMultiOutputRegressor).
- set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') DecisionTreeRegressor[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') DecisionTreeRegressor[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
Gallery examples#
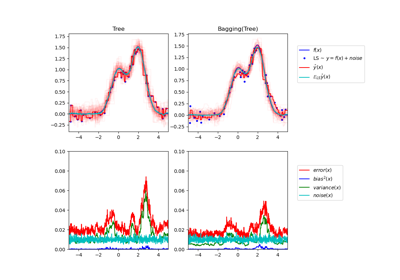
Single estimator versus bagging: bias-variance decomposition
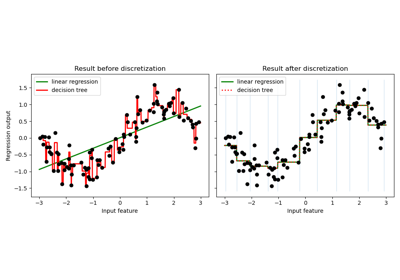
Using KBinsDiscretizer to discretize continuous features