GaussianNB#
- class sklearn.naive_bayes.GaussianNB(*, priors=None, var_smoothing=1e-09)[source]#
Gaussian Naive Bayes (GaussianNB).
Can perform online updates to model parameters via
partial_fit. For details on algorithm used to update feature means and variance online, see Stanford CS tech report STAN-CS-79-773 by Chan, Golub, and LeVeque.Read more in the User Guide.
- Parameters:
- priorsarray-like of shape (n_classes,), default=None
Prior probabilities of the classes. If specified, the priors are not adjusted according to the data.
- var_smoothingfloat, default=1e-9
Portion of the largest variance of all features that is added to variances for calculation stability.
Added in version 0.20.
- Attributes:
- class_count_ndarray of shape (n_classes,)
number of training samples observed in each class.
- class_prior_ndarray of shape (n_classes,)
probability of each class.
- classes_ndarray of shape (n_classes,)
class labels known to the classifier.
- epsilon_float
absolute additive value to variances.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
- var_ndarray of shape (n_classes, n_features)
Variance of each feature per class.
Added in version 1.0.
- theta_ndarray of shape (n_classes, n_features)
mean of each feature per class.
See also
BernoulliNBNaive Bayes classifier for multivariate Bernoulli models.
CategoricalNBNaive Bayes classifier for categorical features.
ComplementNBComplement Naive Bayes classifier.
MultinomialNBNaive Bayes classifier for multinomial models.
Examples
>>> import numpy as np >>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) >>> Y = np.array([1, 1, 1, 2, 2, 2]) >>> from sklearn.naive_bayes import GaussianNB >>> clf = GaussianNB() >>> clf.fit(X, Y) GaussianNB() >>> print(clf.predict([[-0.8, -1]])) [1] >>> clf_pf = GaussianNB() >>> clf_pf.partial_fit(X, Y, np.unique(Y)) GaussianNB() >>> print(clf_pf.predict([[-0.8, -1]])) [1]
- fit(X, y, sample_weight=None)[source]#
Fit Gaussian Naive Bayes according to X, y.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Training vectors, where
n_samplesis the number of samples andn_featuresis the number of features.- yarray-like of shape (n_samples,)
Target values.
- sample_weightarray-like of shape (n_samples,), default=None
Weights applied to individual samples (1. for unweighted).
Added in version 0.17: Gaussian Naive Bayes supports fitting with sample_weight.
- Returns:
- selfobject
Returns the instance itself.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- partial_fit(X, y, classes=None, sample_weight=None)[source]#
Incremental fit on a batch of samples.
This method is expected to be called several times consecutively on different chunks of a dataset so as to implement out-of-core or online learning.
This is especially useful when the whole dataset is too big to fit in memory at once.
This method has some performance and numerical stability overhead, hence it is better to call partial_fit on chunks of data that are as large as possible (as long as fitting in the memory budget) to hide the overhead.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Training vectors, where
n_samplesis the number of samples andn_featuresis the number of features.- yarray-like of shape (n_samples,)
Target values.
- classesarray-like of shape (n_classes,), default=None
List of all the classes that can possibly appear in the y vector.
Must be provided at the first call to partial_fit, can be omitted in subsequent calls.
- sample_weightarray-like of shape (n_samples,), default=None
Weights applied to individual samples (1. for unweighted).
Added in version 0.17.
- Returns:
- selfobject
Returns the instance itself.
- predict(X)[source]#
Perform classification on an array of test vectors X.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The input samples.
- Returns:
- Cndarray of shape (n_samples,)
Predicted target values for X.
- predict_joint_log_proba(X)[source]#
Return joint log probability estimates for the test vector X.
For each row x of X and class y, the joint log probability is given by
log P(x, y) = log P(y) + log P(x|y),wherelog P(y)is the class prior probability andlog P(x|y)is the class-conditional probability.- Parameters:
- Xarray-like of shape (n_samples, n_features)
The input samples.
- Returns:
- Cndarray of shape (n_samples, n_classes)
Returns the joint log-probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute classes_.
- predict_log_proba(X)[source]#
Return log-probability estimates for the test vector X.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The input samples.
- Returns:
- Carray-like of shape (n_samples, n_classes)
Returns the log-probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute classes_.
- predict_proba(X)[source]#
Return probability estimates for the test vector X.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The input samples.
- Returns:
- Carray-like of shape (n_samples, n_classes)
Returns the probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute classes_.
- score(X, y, sample_weight=None)[source]#
Return accuracy on provided data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True labels for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
Mean accuracy of
self.predict(X)w.r.t.y.
- set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') GaussianNB[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_partial_fit_request(*, classes: bool | None | str = '$UNCHANGED$', sample_weight: bool | None | str = '$UNCHANGED$') GaussianNB[source]#
Configure whether metadata should be requested to be passed to the
partial_fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed topartial_fitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it topartial_fit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- classesstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
classesparameter inpartial_fit.- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inpartial_fit.
- Returns:
- selfobject
The updated object.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') GaussianNB[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
Gallery examples#
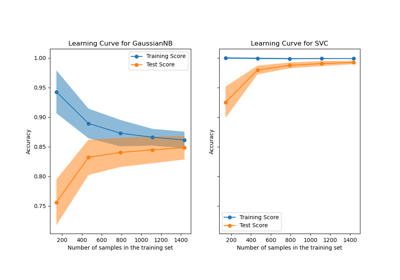
Plotting Learning Curves and Checking Models’ Scalability