RationalQuadratic#
- class sklearn.gaussian_process.kernels.RationalQuadratic(length_scale=1.0, alpha=1.0, length_scale_bounds=(1e-05, 100000.0), alpha_bounds=(1e-05, 100000.0))[source]#
Rational Quadratic kernel.
The RationalQuadratic kernel can be seen as a scale mixture (an infinite sum) of RBF kernels with different characteristic length scales. It is parameterized by a length scale parameter \(l>0\) and a scale mixture parameter \(\alpha>0\). Only the isotropic variant where length_scale \(l\) is a scalar is supported at the moment. The kernel is given by:
\[k(x_i, x_j) = \left( 1 + \frac{d(x_i, x_j)^2 }{ 2\alpha l^2}\right)^{-\alpha}\]where \(\alpha\) is the scale mixture parameter, \(l\) is the length scale of the kernel and \(d(\cdot,\cdot)\) is the Euclidean distance. For advice on how to set the parameters, see e.g. [1].
Read more in the User Guide.
Added in version 0.18.
- Parameters:
- length_scalefloat > 0, default=1.0
The length scale of the kernel.
- alphafloat > 0, default=1.0
Scale mixture parameter
- length_scale_boundspair of floats >= 0 or “fixed”, default=(1e-5, 1e5)
The lower and upper bound on ‘length_scale’. If set to “fixed”, ‘length_scale’ cannot be changed during hyperparameter tuning.
- alpha_boundspair of floats >= 0 or “fixed”, default=(1e-5, 1e5)
The lower and upper bound on ‘alpha’. If set to “fixed”, ‘alpha’ cannot be changed during hyperparameter tuning.
References
Examples
>>> from sklearn.datasets import load_iris >>> from sklearn.gaussian_process import GaussianProcessClassifier >>> from sklearn.gaussian_process.kernels import RationalQuadratic >>> X, y = load_iris(return_X_y=True) >>> kernel = RationalQuadratic(length_scale=1.0, alpha=1.5) >>> gpc = GaussianProcessClassifier(kernel=kernel, ... random_state=0).fit(X, y) >>> gpc.score(X, y) 0.9733 >>> gpc.predict_proba(X[:2,:]) array([[0.8881, 0.0566, 0.05518], [0.8678, 0.0707 , 0.0614]])
- __call__(X, Y=None, eval_gradient=False)[source]#
Return the kernel k(X, Y) and optionally its gradient.
- Parameters:
- Xndarray of shape (n_samples_X, n_features)
Left argument of the returned kernel k(X, Y)
- Yndarray of shape (n_samples_Y, n_features), default=None
Right argument of the returned kernel k(X, Y). If None, k(X, X) if evaluated instead.
- eval_gradientbool, default=False
Determines whether the gradient with respect to the log of the kernel hyperparameter is computed. Only supported when Y is None.
- Returns:
- Kndarray of shape (n_samples_X, n_samples_Y)
Kernel k(X, Y)
- K_gradientndarray of shape (n_samples_X, n_samples_X, n_dims)
The gradient of the kernel k(X, X) with respect to the log of the hyperparameter of the kernel. Only returned when eval_gradient is True.
- property bounds#
Returns the log-transformed bounds on the theta.
- Returns:
- boundsndarray of shape (n_dims, 2)
The log-transformed bounds on the kernel’s hyperparameters theta
- clone_with_theta(theta)[source]#
Returns a clone of self with given hyperparameters theta.
- Parameters:
- thetandarray of shape (n_dims,)
The hyperparameters
- diag(X)[source]#
Returns the diagonal of the kernel k(X, X).
The result of this method is identical to np.diag(self(X)); however, it can be evaluated more efficiently since only the diagonal is evaluated.
- Parameters:
- Xndarray of shape (n_samples_X, n_features)
Left argument of the returned kernel k(X, Y)
- Returns:
- K_diagndarray of shape (n_samples_X,)
Diagonal of kernel k(X, X)
- get_params(deep=True)[source]#
Get parameters of this kernel.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- property hyperparameters#
Returns a list of all hyperparameter specifications.
- property n_dims#
Returns the number of non-fixed hyperparameters of the kernel.
- property requires_vector_input#
Returns whether the kernel is defined on fixed-length feature vectors or generic objects. Defaults to True for backward compatibility.
- set_params(**params)[source]#
Set the parameters of this kernel.
The method works on simple kernels as well as on nested kernels. The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.- Returns:
- self
- property theta#
Returns the (flattened, log-transformed) non-fixed hyperparameters.
Note that theta are typically the log-transformed values of the kernel’s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.
- Returns:
- thetandarray of shape (n_dims,)
The non-fixed, log-transformed hyperparameters of the kernel
Gallery examples#
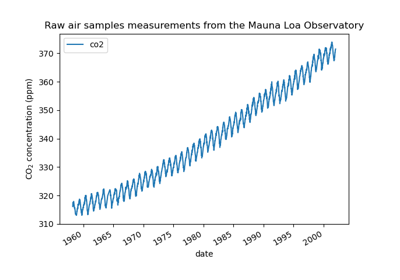
Forecasting of CO2 level on Mona Loa dataset using Gaussian process regression (GPR)
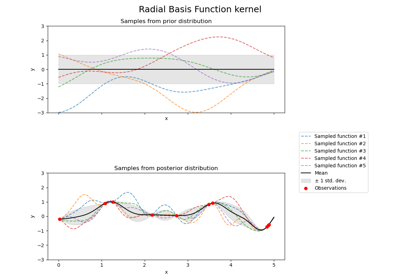
Illustration of prior and posterior Gaussian process for different kernels