GraphicalLassoCV#
- class sklearn.covariance.GraphicalLassoCV(*, alphas=4, n_refinements=4, cv=None, tol=0.0001, enet_tol=0.0001, max_iter=100, mode='cd', n_jobs=None, verbose=False, eps=np.float64(2.220446049250313e-16), assume_centered=False)[source]#
Sparse inverse covariance w/ cross-validated choice of the l1 penalty.
See glossary entry for cross-validation estimator.
Read more in the User Guide.
Changed in version v0.20: GraphLassoCV has been renamed to GraphicalLassoCV
- Parameters:
- alphasint or array-like of shape (n_alphas,), dtype=float, default=4
If an integer is given, it fixes the number of points on the grids of alpha to be used. If a list is given, it gives the grid to be used. See the notes in the class docstring for more details. Range is [1, inf) for an integer. Range is (0, inf] for an array-like of floats.
- n_refinementsint, default=4
The number of times the grid is refined. Not used if explicit values of alphas are passed. Range is [1, inf).
- cvint, cross-validation generator or iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
None, to use the default 5-fold cross-validation,
integer, to specify the number of folds.
An iterable yielding (train, test) splits as arrays of indices.
For integer/None inputs
KFoldis used.Refer User Guide for the various cross-validation strategies that can be used here.
Changed in version 0.20:
cvdefault value if None changed from 3-fold to 5-fold.- tolfloat, default=1e-4
The tolerance to declare convergence: if the dual gap goes below this value, iterations are stopped. Range is (0, inf].
- enet_tolfloat, default=1e-4
The tolerance for the elastic net solver used to calculate the descent direction. This parameter controls the accuracy of the search direction for a given column update, not of the overall parameter estimate. Only used for mode=’cd’. Range is (0, inf].
- max_iterint, default=100
Maximum number of iterations.
- mode{‘cd’, ‘lars’}, default=’cd’
The Lasso solver to use: coordinate descent or LARS. Use LARS for very sparse underlying graphs, where number of features is greater than number of samples. Elsewhere prefer cd which is more numerically stable.
- n_jobsint, default=None
Number of jobs to run in parallel.
Nonemeans 1 unless in ajoblib.parallel_backendcontext.-1means using all processors. See Glossary for more details.Changed in version v0.20:
n_jobsdefault changed from 1 to None- verbosebool, default=False
If verbose is True, the objective function and duality gap are printed at each iteration.
- epsfloat, default=eps
The machine-precision regularization in the computation of the Cholesky diagonal factors. Increase this for very ill-conditioned systems. Default is
np.finfo(np.float64).eps.Added in version 1.3.
- assume_centeredbool, default=False
If True, data are not centered before computation. Useful when working with data whose mean is almost, but not exactly zero. If False, data are centered before computation.
- Attributes:
- location_ndarray of shape (n_features,)
Estimated location, i.e. the estimated mean.
- covariance_ndarray of shape (n_features, n_features)
Estimated covariance matrix.
- precision_ndarray of shape (n_features, n_features)
Estimated precision matrix (inverse covariance).
- costs_list of (objective, dual_gap) pairs
The list of values of the objective function and the dual gap at each iteration. Returned only if return_costs is True.
Added in version 1.3.
- alpha_float
Penalization parameter selected.
- cv_results_dict of ndarrays
A dict with keys:
- alphasndarray of shape (n_alphas,)
All penalization parameters explored.
- split(k)_test_scorendarray of shape (n_alphas,)
Log-likelihood score on left-out data across (k)th fold.
Added in version 1.0.
- mean_test_scorendarray of shape (n_alphas,)
Mean of scores over the folds.
Added in version 1.0.
- std_test_scorendarray of shape (n_alphas,)
Standard deviation of scores over the folds.
Added in version 1.0.
- n_iter_int
Number of iterations run for the optimal alpha.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
graphical_lassoL1-penalized covariance estimator.
GraphicalLassoSparse inverse covariance estimation with an l1-penalized estimator.
Notes
The search for the optimal penalization parameter (
alpha) is done on an iteratively refined grid: first the cross-validated scores on a grid are computed, then a new refined grid is centered around the maximum, and so on.One of the challenges which is faced here is that the solvers can fail to converge to a well-conditioned estimate. The corresponding values of
alphathen come out as missing values, but the optimum may be close to these missing values.In
fit, once the best parameteralphais found through cross-validation, the model is fit again using the entire training set.Examples
>>> import numpy as np >>> from sklearn.covariance import GraphicalLassoCV >>> true_cov = np.array([[0.8, 0.0, 0.2, 0.0], ... [0.0, 0.4, 0.0, 0.0], ... [0.2, 0.0, 0.3, 0.1], ... [0.0, 0.0, 0.1, 0.7]]) >>> np.random.seed(0) >>> X = np.random.multivariate_normal(mean=[0, 0, 0, 0], ... cov=true_cov, ... size=200) >>> cov = GraphicalLassoCV().fit(X) >>> np.around(cov.covariance_, decimals=3) array([[0.816, 0.051, 0.22 , 0.017], [0.051, 0.364, 0.018, 0.036], [0.22 , 0.018, 0.322, 0.094], [0.017, 0.036, 0.094, 0.69 ]]) >>> np.around(cov.location_, decimals=3) array([0.073, 0.04 , 0.038, 0.143])
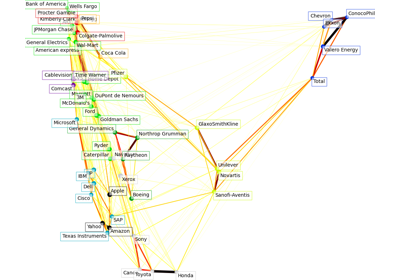
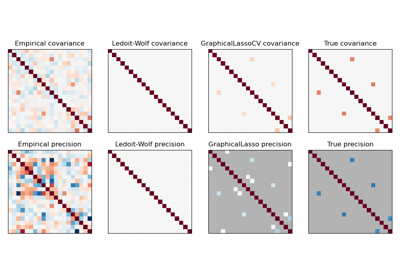
For an example comparing
sklearn.covariance.GraphicalLassoCV,sklearn.covariance.ledoit_wolfshrinkage and the empirical covariance on high-dimensional gaussian data, see Sparse inverse covariance estimation.- error_norm(comp_cov, norm='frobenius', scaling=True, squared=True)[source]#
Compute the Mean Squared Error between two covariance estimators.
- Parameters:
- comp_covarray-like of shape (n_features, n_features)
The covariance to compare with.
- norm{“frobenius”, “spectral”}, default=”frobenius”
The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error
(comp_cov - self.covariance_).- scalingbool, default=True
If True (default), the squared error norm is divided by n_features. If False, the squared error norm is not rescaled.
- squaredbool, default=True
Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.
- Returns:
- resultfloat
The Mean Squared Error (in the sense of the Frobenius norm) between
selfandcomp_covcovariance estimators.
- fit(X, y=None, **params)[source]#
Fit the GraphicalLasso covariance model to X.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Data from which to compute the covariance estimate.
- yIgnored
Not used, present for API consistency by convention.
- **paramsdict, default=None
Parameters to be passed to the CV splitter and the cross_val_score function.
Added in version 1.5: Only available if
enable_metadata_routing=True, which can be set by usingsklearn.set_config(enable_metadata_routing=True). See Metadata Routing User Guide for more details.
- Returns:
- selfobject
Returns the instance itself.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
Added in version 1.5.
- Returns:
- routingMetadataRouter
A
MetadataRouterencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- get_precision()[source]#
Getter for the precision matrix.
- Returns:
- precision_array-like of shape (n_features, n_features)
The precision matrix associated to the current covariance object.
- mahalanobis(X)[source]#
Compute the squared Mahalanobis distances of given observations.
For a detailed example of how outliers affects the Mahalanobis distance, see Robust covariance estimation and Mahalanobis distances relevance.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.
- Returns:
- distndarray of shape (n_samples,)
Squared Mahalanobis distances of the observations.
- score(X_test, y=None)[source]#
Compute the log-likelihood of
X_testunder the estimated Gaussian model.The Gaussian model is defined by its mean and covariance matrix which are represented respectively by
self.location_andself.covariance_.- Parameters:
- X_testarray-like of shape (n_samples, n_features)
Test data of which we compute the likelihood, where
n_samplesis the number of samples andn_featuresis the number of features.X_testis assumed to be drawn from the same distribution than the data used in fit (including centering).- yIgnored
Not used, present for API consistency by convention.
- Returns:
- resfloat
The log-likelihood of
X_testwithself.location_andself.covariance_as estimators of the Gaussian model mean and covariance matrix respectively.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.