adjusted_rand_score#
- sklearn.metrics.adjusted_rand_score(labels_true, labels_pred)[source]#
Rand index adjusted for chance.
The Rand Index computes a similarity measure between two clusterings by considering all pairs of samples and counting pairs that are assigned in the same or different clusters in the predicted and true clusterings.
The raw RI score is then “adjusted for chance” into the ARI score using the following scheme:
ARI = (RI - Expected_RI) / (max(RI) - Expected_RI)
The adjusted Rand index is thus ensured to have a value close to 0.0 for random labeling independently of the number of clusters and samples and exactly 1.0 when the clusterings are identical (up to a permutation). The adjusted Rand index is bounded below by -0.5 for especially discordant clusterings.
ARI is a symmetric measure:
adjusted_rand_score(a, b) == adjusted_rand_score(b, a)
Read more in the User Guide.
- Parameters:
- labels_truearray-like of shape (n_samples,), dtype=int
Ground truth class labels to be used as a reference.
- labels_predarray-like of shape (n_samples,), dtype=int
Cluster labels to evaluate.
- Returns:
- ARIfloat
Similarity score between -0.5 and 1.0. Random labelings have an ARI close to 0.0. 1.0 stands for perfect match.
See also
adjusted_mutual_info_scoreAdjusted Mutual Information.
References
[Hubert1985]L. Hubert and P. Arabie, Comparing Partitions, Journal of Classification 1985 https://link.springer.com/article/10.1007%2FBF01908075
[Steinley2004]D. Steinley, Properties of the Hubert-Arabie adjusted Rand index, Psychological Methods 2004
Examples
Perfectly matching labelings have a score of 1 even
>>> from sklearn.metrics.cluster import adjusted_rand_score >>> adjusted_rand_score([0, 0, 1, 1], [0, 0, 1, 1]) 1.0 >>> adjusted_rand_score([0, 0, 1, 1], [1, 1, 0, 0]) 1.0
Labelings that assign all classes members to the same clusters are complete but may not always be pure, hence penalized:
>>> adjusted_rand_score([0, 0, 1, 2], [0, 0, 1, 1]) 0.57
ARI is symmetric, so labelings that have pure clusters with members coming from the same classes but unnecessary splits are penalized:
>>> adjusted_rand_score([0, 0, 1, 1], [0, 0, 1, 2]) 0.57
If classes members are completely split across different clusters, the assignment is totally incomplete, hence the ARI is very low:
>>> adjusted_rand_score([0, 0, 0, 0], [0, 1, 2, 3]) 0.0
ARI may take a negative value for especially discordant labelings that are a worse choice than the expected value of random labels:
>>> adjusted_rand_score([0, 0, 1, 1], [0, 1, 0, 1]) -0.5
See Adjustment for chance in clustering performance evaluation for a more detailed example.
Gallery examples#
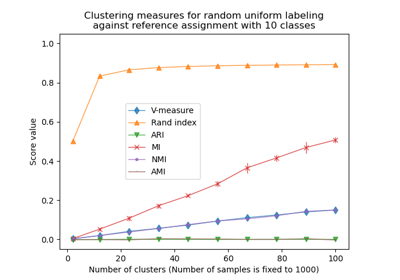
Adjustment for chance in clustering performance evaluation
A demo of K-Means clustering on the handwritten digits data