QuadraticDiscriminantAnalysis

class sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis(*, solver='svd', shrinkage=None, priors=None, reg_param=0.0, store_covariance=False, tol=0.0001, covariance_estimator=None)

Quadratic Discriminant Analysis.

A classifier with a quadratic decision boundary, generated by fitting class conditional densities to the data and using Bayes’ rule.

The model fits a Gaussian density to each class.

Added in version 0.17.

For a comparison between QuadraticDiscriminantAnalysis and LinearDiscriminantAnalysis, see Linear and Quadratic Discriminant Analysis with covariance ellipsoid.

Read more in the User Guide.

Parameters:

solver{‘svd’, ‘eigen’}, default=’svd’

Solver to use, possible values:

• ‘svd’: Singular value decomposition (default). Does not compute the covariance matrix, therefore this solver is recommended for data with a large number of features.

• ‘eigen’: Eigenvalue decomposition. Can be combined with shrinkage or custom covariance estimator.

shrinkage‘auto’ or float, default=None

Shrinkage parameter, possible values:

• None: no shrinkage (default).

• ‘auto’: automatic shrinkage using the Ledoit-Wolf lemma.

• float between 0 and 1: fixed shrinkage parameter.

Enabling shrinkage is expected to improve the model when some classes have a relatively small number of training data points compared to the number of features by mitigating overfitting during the covariance estimation step.

This should be left to None if covariance_estimator is used. Note that shrinkage works only with ‘eigen’ solver.

priorsarray-like of shape (n_classes,), default=None

Class priors. By default, the class proportions are inferred from the training data.

reg_paramfloat, default=0.0

Regularizes the per-class covariance estimates by transforming S2 as S2 = (1 - reg_param) * S2 + reg_param * np.eye(n_features), where S2 corresponds to the scaling_ attribute of a given class.

store_covariancebool, default=False

If True, the class covariance matrices are explicitly computed and stored in the self.covariance_ attribute.

Added in version 0.17.

tolfloat, default=1.0e-4

Absolute threshold for the covariance matrix to be considered rank deficient after applying some regularization (see reg_param) to each Sk where Sk represents covariance matrix for k-th class. This parameter does not affect the predictions. It controls when a warning is raised if the covariance matrix is not full rank.

Added in version 0.17.

covariance_estimatorcovariance estimator, default=None

If not None, covariance_estimator is used to estimate the covariance matrices instead of relying on the empirical covariance estimator (with potential shrinkage). The object should have a fit method and a covariance_ attribute like the estimators in sklearn.covariance. If None the shrinkage parameter drives the estimate.

This should be left to None if shrinkage is used. Note that covariance_estimator works only with the ‘eigen’ solver.

Attributes:

covariance_list of len n_classes of ndarray of shape (n_features, n_features)

For each class, gives the covariance matrix estimated using the samples of that class. The estimations are unbiased. Only present if store_covariance is True.

means_array-like of shape (n_classes, n_features)

Class-wise means.

priors_array-like of shape (n_classes,)

Class priors (sum to 1).

rotations_list of len n_classes of ndarray of shape (n_features, n_k)

For each class k an array of shape (n_features, n_k), where n_k = min(n_features, number of elements in class k) It is the rotation of the Gaussian distribution, i.e. its principal axis. It corresponds to V, the matrix of eigenvectors coming from the SVD of Xk = U S Vt where Xk is the centered matrix of samples from class k.

scalings_list of len n_classes of ndarray of shape (n_k,)

For each class, contains the scaling of the Gaussian distributions along its principal axes, i.e. the variance in the rotated coordinate system. It corresponds to S^2 / (n_samples - 1), where S is the diagonal matrix of singular values from the SVD of Xk, where Xk is the centered matrix of samples from class k.

classes_ndarray of shape (n_classes,)

Unique class labels.

n_features_in_int

Number of features seen during fit.

Added in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

Added in version 1.0.

See also

LinearDiscriminantAnalysis

Linear Discriminant Analysis.

Examples

>>> from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = QuadraticDiscriminantAnalysis()
>>> clf.fit(X, y)
QuadraticDiscriminantAnalysis()
>>> print(clf.predict([[-0.8, -1]]))
[1]

decision_function(X)

Apply decision function to an array of samples.

The decision function is equal (up to a constant factor) to the log-posterior of the model, i.e. log p(y = k | x). In a binary classification setting this instead corresponds to the difference log p(y = 1 | x) - log p(y = 0 | x). See Mathematical formulation of the LDA and QDA classifiers.

Parameters:

Xarray-like of shape (n_samples, n_features)

Array of samples (test vectors).

Returns:

Cndarray of shape (n_samples,) or (n_samples, n_classes)

Decision function values related to each class, per sample. In the two-class case, the shape is (n_samples,), giving the log likelihood ratio of the positive class.

fit(X, y)

Fit the model according to the given training data and parameters.

Changed in version 0.19: store_covariances has been moved to main constructor as store_covariance.

Changed in version 0.19: tol has been moved to main constructor.

Parameters:

Xarray-like of shape (n_samples, n_features)

Training vector, where n_samples is the number of samples and n_features is the number of features.

yarray-like of shape (n_samples,)

Target values (integers).

Returns:

selfobject

Fitted estimator.

get_metadata_routing()

Get metadata routing of this object.

Please check User Guide on how the routing mechanism works.

Returns:

routingMetadataRequest

A MetadataRequest encapsulating routing information.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

predict(X)

Perform classification on an array of vectors X.

Returns the class label for each sample.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

Input vectors, where n_samples is the number of samples and n_features is the number of features.

Returns:

y_predndarray of shape (n_samples,)

Class label for each sample.

predict_log_proba(X)

Estimate log class probabilities.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

Input data.

Returns:

y_log_probandarray of shape (n_samples, n_classes)

Estimated log probabilities.

predict_proba(X)

Estimate class probabilities.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

Input data.

Returns:

y_probandarray of shape (n_samples, n_classes)

Probability estimate of the sample for each class in the model, where classes are ordered as they are in self.classes_.

score(X, y, sample_weight=None)

Return accuracy on provided data and labels.

In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.

Parameters:

Xarray-like of shape (n_samples, n_features)

Test samples.

yarray-like of shape (n_samples,) or (n_samples, n_outputs)

True labels for X.

sample_weightarray-like of shape (n_samples,), default=None

Sample weights.

Returns:

scorefloat

Mean accuracy of self.predict(X) w.r.t. y.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') → QuadraticDiscriminantAnalysis

Configure whether metadata should be requested to be passed to the score method.

Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with enable_metadata_routing=True (see sklearn.set_config). Please check the User Guide on how the routing mechanism works.

The options for each parameter are:

• True: metadata is requested, and passed to score if provided. The request is ignored if metadata is not provided.

• False: metadata is not requested and the meta-estimator will not pass it to score.

• None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.

• str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

Added in version 1.3.

Parameters:

sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED

Metadata routing for sample_weight parameter in score.

Returns:

selfobject

The updated object.

Gallery examples

Classifier comparison

Classifier comparison

Linear and Quadratic Discriminant Analysis with covariance ellipsoid

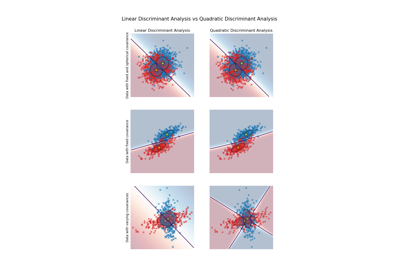
Linear and Quadratic Discriminant Analysis with covariance ellipsoid