NeighborhoodComponentsAnalysis#
- class sklearn.neighbors.NeighborhoodComponentsAnalysis(n_components=None, *, init='auto', warm_start=False, max_iter=50, tol=1e-05, callback=None, verbose=0, random_state=None)[source]#
Neighborhood Components Analysis.
Neighborhood Component Analysis (NCA) is a machine learning algorithm for metric learning. It learns a linear transformation in a supervised fashion to improve the classification accuracy of a stochastic nearest neighbors rule in the transformed space.
Read more in the User Guide.
- Parameters:
- n_componentsint, default=None
Preferred dimensionality of the projected space. If None it will be set to
n_features.- init{‘auto’, ‘pca’, ‘lda’, ‘identity’, ‘random’} or ndarray of shape (n_features_a, n_features_b), default=’auto’
Initialization of the linear transformation. Possible options are
'auto','pca','lda','identity','random', and a numpy array of shape(n_features_a, n_features_b).'auto'Depending on
n_components, the most reasonable initialization is chosen. Ifn_components <= min(n_features, n_classes - 1)we use'lda', as it uses labels information. If not, butn_components < min(n_features, n_samples), we use'pca', as it projects data in meaningful directions (those of higher variance). Otherwise, we just use'identity'.
'lda'min(n_components, n_classes)most discriminative components of the inputs passed tofitwill be used to initialize the transformation. (Ifn_components > n_classes, the rest of the components will be zero.) (SeeLinearDiscriminantAnalysis)
'identity'If
n_componentsis strictly smaller than the dimensionality of the inputs passed tofit, the identity matrix will be truncated to the firstn_componentsrows.
'random'The initial transformation will be a random array of shape
(n_components, n_features). Each value is sampled from the standard normal distribution.
- numpy array
n_features_bmust match the dimensionality of the inputs passed tofitand n_features_a must be less than or equal to that. Ifn_componentsis notNone,n_features_amust match it.
- warm_startbool, default=False
If
Trueandfithas been called before, the solution of the previous call tofitis used as the initial linear transformation (n_componentsandinitwill be ignored).- max_iterint, default=50
Maximum number of iterations in the optimization.
- tolfloat, default=1e-5
Convergence tolerance for the optimization.
- callbackcallable, default=None
If not
None, this function is called after every iteration of the optimizer, taking as arguments the current solution (flattened transformation matrix) and the number of iterations. This might be useful in case one wants to examine or store the transformation found after each iteration.- verboseint, default=0
If 0, no progress messages will be printed. If 1, progress messages will be printed to stdout. If > 1, progress messages will be printed and the
dispparameter ofscipy.optimize.minimizewill be set toverbose - 2.- random_stateint or numpy.RandomState, default=None
A pseudo random number generator object or a seed for it if int. If
init='random',random_stateis used to initialize the random transformation. Ifinit='pca',random_stateis passed as an argument to PCA when initializing the transformation. Pass an int for reproducible results across multiple function calls. See Glossary.
- Attributes:
- components_ndarray of shape (n_components, n_features)
The linear transformation learned during fitting.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- n_iter_int
Counts the number of iterations performed by the optimizer.
- random_state_numpy.RandomState
Pseudo random number generator object used during initialization.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
sklearn.discriminant_analysis.LinearDiscriminantAnalysisLinear Discriminant Analysis.
sklearn.decomposition.PCAPrincipal component analysis (PCA).
References
[1]J. Goldberger, G. Hinton, S. Roweis, R. Salakhutdinov. “Neighbourhood Components Analysis”. Advances in Neural Information Processing Systems. 17, 513-520, 2005. https://www.cs.toronto.edu/~rsalakhu/papers/ncanips.pdf
[2]Wikipedia entry on Neighborhood Components Analysis https://en.wikipedia.org/wiki/Neighbourhood_components_analysis
Examples
>>> from sklearn.neighbors import NeighborhoodComponentsAnalysis >>> from sklearn.neighbors import KNeighborsClassifier >>> from sklearn.datasets import load_iris >>> from sklearn.model_selection import train_test_split >>> X, y = load_iris(return_X_y=True) >>> X_train, X_test, y_train, y_test = train_test_split(X, y, ... stratify=y, test_size=0.7, random_state=42) >>> nca = NeighborhoodComponentsAnalysis(random_state=42) >>> nca.fit(X_train, y_train) NeighborhoodComponentsAnalysis(...) >>> knn = KNeighborsClassifier(n_neighbors=3) >>> knn.fit(X_train, y_train) KNeighborsClassifier(...) >>> print(knn.score(X_test, y_test)) 0.933333... >>> knn.fit(nca.transform(X_train), y_train) KNeighborsClassifier(...) >>> print(knn.score(nca.transform(X_test), y_test)) 0.961904...
- fit(X, y)[source]#
Fit the model according to the given training data.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The training samples.
- yarray-like of shape (n_samples,)
The corresponding training labels.
- Returns:
- selfobject
Fitted estimator.
- fit_transform(X, y=None, **fit_params)[source]#
Fit to data, then transform it.
Fits transformer to
Xandywith optional parametersfit_paramsand returns a transformed version ofX.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Input samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None
Target values (None for unsupervised transformations).
- **fit_paramsdict
Additional fit parameters. Pass only if the estimator accepts additional params in its
fitmethod.
- Returns:
- X_newndarray array of shape (n_samples, n_features_new)
Transformed array.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are:
["class_name0", "class_name1", "class_name2"].- Parameters:
- input_featuresarray-like of str or None, default=None
Only used to validate feature names with the names seen in
fit.
- Returns:
- feature_names_outndarray of str objects
Transformed feature names.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
Gallery examples#

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…
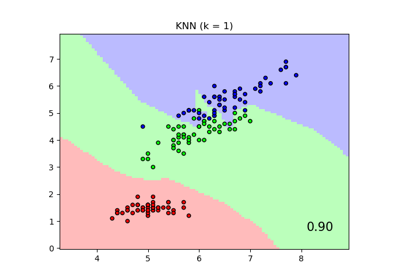
Comparing Nearest Neighbors with and without Neighborhood Components Analysis
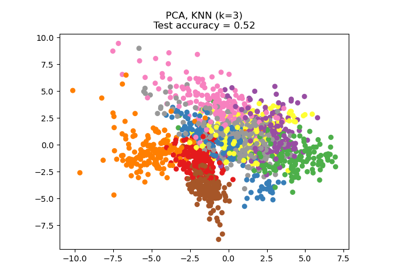
Dimensionality Reduction with Neighborhood Components Analysis