MiniBatchNMF#
- class sklearn.decomposition.MiniBatchNMF(n_components='auto', *, init=None, batch_size=1024, beta_loss='frobenius', tol=0.0001, max_no_improvement=10, max_iter=200, alpha_W=0.0, alpha_H='same', l1_ratio=0.0, forget_factor=0.7, fresh_restarts=False, fresh_restarts_max_iter=30, transform_max_iter=None, random_state=None, verbose=0)[source]#
Mini-Batch Non-Negative Matrix Factorization (NMF).
Added in version 1.1.
Find two non-negative matrices, i.e. matrices with all non-negative elements, (
W,H) whose product approximates the non-negative matrixX. This factorization can be used for example for dimensionality reduction, source separation or topic extraction.The objective function is:
\[ \begin{align}\begin{aligned}L(W, H) &= 0.5 * ||X - WH||_{loss}^2\\ &+ alpha\_W * l1\_ratio * n\_features * ||vec(W)||_1\\ &+ alpha\_H * l1\_ratio * n\_samples * ||vec(H)||_1\\ &+ 0.5 * alpha\_W * (1 - l1\_ratio) * n\_features * ||W||_{Fro}^2\\ &+ 0.5 * alpha\_H * (1 - l1\_ratio) * n\_samples * ||H||_{Fro}^2,\end{aligned}\end{align} \]where \(||A||_{Fro}^2 = \sum_{i,j} A_{ij}^2\) (Frobenius norm) and \(||vec(A)||_1 = \sum_{i,j} abs(A_{ij})\) (Elementwise L1 norm).
The generic norm \(||X - WH||_{loss}^2\) may represent the Frobenius norm or another supported beta-divergence loss. The choice between options is controlled by the
beta_lossparameter.The objective function is minimized with an alternating minimization of
WandH.Note that the transformed data is named
Wand the components matrix is namedH. In the NMF literature, the naming convention is usually the opposite since the data matrixXis transposed.Read more in the User Guide.
- Parameters:
- n_componentsint or {‘auto’} or None, default=’auto’
Number of components. If
None, all features are kept. Ifn_components='auto', the number of components is automatically inferred from W or H shapes.Changed in version 1.4: Added
'auto'value.Changed in version 1.6: Default value changed from
Noneto'auto'.- init{‘random’, ‘nndsvd’, ‘nndsvda’, ‘nndsvdar’, ‘custom’}, default=None
Method used to initialize the procedure. Valid options:
None: ‘nndsvda’ ifn_components <= min(n_samples, n_features), otherwise random.'random': non-negative random matrices, scaled with:sqrt(X.mean() / n_components)'nndsvd': Nonnegative Double Singular Value Decomposition (NNDSVD) initialization (better for sparseness).'nndsvda': NNDSVD with zeros filled with the average of X (better when sparsity is not desired).'nndsvdar'NNDSVD with zeros filled with small random values (generally faster, less accurate alternative to NNDSVDa for when sparsity is not desired).'custom': Use custom matricesWandHwhich must both be provided.
- batch_sizeint, default=1024
Number of samples in each mini-batch. Large batch sizes give better long-term convergence at the cost of a slower start.
- beta_lossfloat or {‘frobenius’, ‘kullback-leibler’, ‘itakura-saito’}, default=’frobenius’
Beta divergence to be minimized, measuring the distance between
Xand the dot productWH. Note that values different from ‘frobenius’ (or 2) and ‘kullback-leibler’ (or 1) lead to significantly slower fits. Note that forbeta_loss <= 0(or ‘itakura-saito’), the input matrixXcannot contain zeros.- tolfloat, default=1e-4
Control early stopping based on the norm of the differences in
Hbetween 2 steps. To disable early stopping based on changes inH, settolto 0.0.- max_no_improvementint, default=10
Control early stopping based on the consecutive number of mini batches that does not yield an improvement on the smoothed cost function. To disable convergence detection based on cost function, set
max_no_improvementto None.- max_iterint, default=200
Maximum number of iterations over the complete dataset before timing out.
- alpha_Wfloat, default=0.0
Constant that multiplies the regularization terms of
W. Set it to zero (default) to have no regularization onW.- alpha_Hfloat or “same”, default=”same”
Constant that multiplies the regularization terms of
H. Set it to zero to have no regularization onH. If “same” (default), it takes the same value asalpha_W.- l1_ratiofloat, default=0.0
The regularization mixing parameter, with 0 <= l1_ratio <= 1. For l1_ratio = 0 the penalty is an elementwise L2 penalty (aka Frobenius Norm). For l1_ratio = 1 it is an elementwise L1 penalty. For 0 < l1_ratio < 1, the penalty is a combination of L1 and L2.
- forget_factorfloat, default=0.7
Amount of rescaling of past information. Its value could be 1 with finite datasets. Choosing values < 1 is recommended with online learning as more recent batches will weight more than past batches.
- fresh_restartsbool, default=False
Whether to completely solve for W at each step. Doing fresh restarts will likely lead to a better solution for a same number of iterations but it is much slower.
- fresh_restarts_max_iterint, default=30
Maximum number of iterations when solving for W at each step. Only used when doing fresh restarts. These iterations may be stopped early based on a small change of W controlled by
tol.- transform_max_iterint, default=None
Maximum number of iterations when solving for W at transform time. If None, it defaults to
max_iter.- random_stateint, RandomState instance or None, default=None
Used for initialisation (when
init== ‘nndsvdar’ or ‘random’), and in Coordinate Descent. Pass an int for reproducible results across multiple function calls. See Glossary.- verbosebool, default=False
Whether to be verbose.
- Attributes:
- components_ndarray of shape (n_components, n_features)
Factorization matrix, sometimes called ‘dictionary’.
- n_components_int
The number of components. It is same as the
n_componentsparameter if it was given. Otherwise, it will be same as the number of features.- reconstruction_err_float
Frobenius norm of the matrix difference, or beta-divergence, between the training data
Xand the reconstructed dataWHfrom the fitted model.- n_iter_int
Actual number of started iterations over the whole dataset.
- n_steps_int
Number of mini-batches processed.
- n_features_in_int
Number of features seen during fit.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.
See also
NMFNon-negative matrix factorization.
MiniBatchDictionaryLearningFinds a dictionary that can best be used to represent data using a sparse code.
References
[1]“Fast local algorithms for large scale nonnegative matrix and tensor factorizations” Cichocki, Andrzej, and P. H. A. N. Anh-Huy. IEICE transactions on fundamentals of electronics, communications and computer sciences 92.3: 708-721, 2009.
[2]“Algorithms for nonnegative matrix factorization with the beta-divergence” Fevotte, C., & Idier, J. (2011). Neural Computation, 23(9).
[3]“Online algorithms for nonnegative matrix factorization with the Itakura-Saito divergence” Lefevre, A., Bach, F., Fevotte, C. (2011). WASPA.
Examples
>>> import numpy as np >>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]]) >>> from sklearn.decomposition import MiniBatchNMF >>> model = MiniBatchNMF(n_components=2, init='random', random_state=0) >>> W = model.fit_transform(X) >>> H = model.components_
- fit(X, y=None, **params)[source]#
Learn a NMF model for the data X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training vector, where
n_samplesis the number of samples andn_featuresis the number of features.- yIgnored
Not used, present for API consistency by convention.
- **paramskwargs
Parameters (keyword arguments) and values passed to the fit_transform instance.
- Returns:
- selfobject
Returns the instance itself.
- fit_transform(X, y=None, W=None, H=None)[source]#
Learn a NMF model for the data X and returns the transformed data.
This is more efficient than calling fit followed by transform.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Data matrix to be decomposed.
- yIgnored
Not used, present here for API consistency by convention.
- Warray-like of shape (n_samples, n_components), default=None
If
init='custom', it is used as initial guess for the solution. IfNone, uses the initialisation method specified ininit.- Harray-like of shape (n_components, n_features), default=None
If
init='custom', it is used as initial guess for the solution. IfNone, uses the initialisation method specified ininit.
- Returns:
- Wndarray of shape (n_samples, n_components)
Transformed data.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are:
["class_name0", "class_name1", "class_name2"].- Parameters:
- input_featuresarray-like of str or None, default=None
Only used to validate feature names with the names seen in
fit.
- Returns:
- feature_names_outndarray of str objects
Transformed feature names.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- inverse_transform(X)[source]#
Transform data back to its original space.
Added in version 0.18.
- Parameters:
- X{ndarray, sparse matrix} of shape (n_samples, n_components)
Transformed data matrix.
- Returns:
- X_originalndarray of shape (n_samples, n_features)
Returns a data matrix of the original shape.
- partial_fit(X, y=None, W=None, H=None)[source]#
Update the model using the data in
Xas a mini-batch.This method is expected to be called several times consecutively on different chunks of a dataset so as to implement out-of-core or online learning.
This is especially useful when the whole dataset is too big to fit in memory at once (see Strategies to scale computationally: bigger data).
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Data matrix to be decomposed.
- yIgnored
Not used, present here for API consistency by convention.
- Warray-like of shape (n_samples, n_components), default=None
If
init='custom', it is used as initial guess for the solution. Only used for the first call topartial_fit.- Harray-like of shape (n_components, n_features), default=None
If
init='custom', it is used as initial guess for the solution. Only used for the first call topartial_fit.
- Returns:
- self
Returns the instance itself.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_partial_fit_request(*, H: bool | None | str = '$UNCHANGED$', W: bool | None | str = '$UNCHANGED$') MiniBatchNMF[source]#
Configure whether metadata should be requested to be passed to the
partial_fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed topartial_fitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it topartial_fit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- Hstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
Hparameter inpartial_fit.- Wstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
Wparameter inpartial_fit.
- Returns:
- selfobject
The updated object.
Gallery examples#
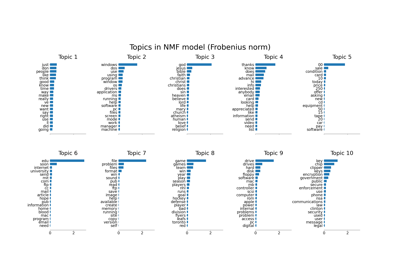
Topic extraction with Non-negative Matrix Factorization and Latent Dirichlet Allocation