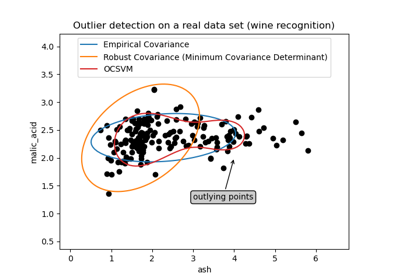
EllipticEnvelope#
- class sklearn.covariance.EllipticEnvelope(*, store_precision=True, assume_centered=False, support_fraction=None, contamination=0.1, random_state=None)[source]#
An object for detecting outliers in a Gaussian distributed dataset.
Read more in the User Guide.
- Parameters:
- store_precisionbool, default=True
Specify if the estimated precision is stored.
- assume_centeredbool, default=False
If True, the support of robust location and covariance estimates is computed, and a covariance estimate is recomputed from it, without centering the data. Useful to work with data whose mean is significantly equal to zero but is not exactly zero. If False, the robust location and covariance are directly computed with the FastMCD algorithm without additional treatment.
- support_fractionfloat, default=None
The proportion of points to be included in the support of the raw MCD estimate. If None, the minimum value of support_fraction will be used within the algorithm:
(n_samples + n_features + 1) / 2 * n_samples. Range is (0, 1).- contaminationfloat, default=0.1
The amount of contamination of the data set, i.e. the proportion of outliers in the data set. Range is (0, 0.5].
- random_stateint, RandomState instance or None, default=None
Determines the pseudo random number generator for shuffling the data. Pass an int for reproducible results across multiple function calls. See Glossary.
- Attributes:
- location_ndarray of shape (n_features,)
Estimated robust location.
- covariance_ndarray of shape (n_features, n_features)
Estimated robust covariance matrix.
- precision_ndarray of shape (n_features, n_features)
Estimated pseudo inverse matrix. (stored only if store_precision is True)
- support_ndarray of shape (n_samples,)
A mask of the observations that have been used to compute the robust estimates of location and shape.
- offset_float
Offset used to define the decision function from the raw scores. We have the relation:
decision_function = score_samples - offset_. The offset depends on the contamination parameter and is defined in such a way we obtain the expected number of outliers (samples with decision function < 0) in training.Added in version 0.20.
- raw_location_ndarray of shape (n_features,)
The raw robust estimated location before correction and re-weighting.
- raw_covariance_ndarray of shape (n_features, n_features)
The raw robust estimated covariance before correction and re-weighting.
- raw_support_ndarray of shape (n_samples,)
A mask of the observations that have been used to compute the raw robust estimates of location and shape, before correction and re-weighting.
- dist_ndarray of shape (n_samples,)
Mahalanobis distances of the training set (on which
fitis called) observations.- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
EmpiricalCovarianceMaximum likelihood covariance estimator.
GraphicalLassoSparse inverse covariance estimation with an l1-penalized estimator.
LedoitWolfLedoitWolf Estimator.
MinCovDetMinimum Covariance Determinant (robust estimator of covariance).
OASOracle Approximating Shrinkage Estimator.
ShrunkCovarianceCovariance estimator with shrinkage.
Notes
Outlier detection from covariance estimation may break or not perform well in high-dimensional settings. In particular, one will always take care to work with
n_samples > n_features ** 2.References
[1]Rousseeuw, P.J., Van Driessen, K. “A fast algorithm for the minimum covariance determinant estimator” Technometrics 41(3), 212 (1999)
Examples
>>> import numpy as np >>> from sklearn.covariance import EllipticEnvelope >>> true_cov = np.array([[.8, .3], ... [.3, .4]]) >>> X = np.random.RandomState(0).multivariate_normal(mean=[0, 0], ... cov=true_cov, ... size=500) >>> cov = EllipticEnvelope(random_state=0).fit(X) >>> # predict returns 1 for an inlier and -1 for an outlier >>> cov.predict([[0, 0], ... [3, 3]]) array([ 1, -1]) >>> cov.covariance_ array([[0.8102, 0.2736], [0.2736, 0.3330]]) >>> cov.location_ array([0.0769 , 0.0397])
- correct_covariance(data)[source]#
Apply a correction to raw Minimum Covariance Determinant estimates.
Correction using the asymptotic correction factor derived by [Croux1999].
- Parameters:
- dataarray-like of shape (n_samples, n_features)
The data matrix, with p features and n samples. The data set must be the one which was used to compute the raw estimates.
- Returns:
- covariance_correctedndarray of shape (n_features, n_features)
Corrected robust covariance estimate.
References
[Croux1999]Influence Function and Efficiency of the Minimum Covariance Determinant Scatter Matrix Estimator, 1999, Journal of Multivariate Analysis, Volume 71, Issue 2, Pages 161-190
- decision_function(X)[source]#
Compute the decision function of the given observations.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The data matrix.
- Returns:
- decisionndarray of shape (n_samples,)
Decision function of the samples. It is equal to the shifted Mahalanobis distances. The threshold for being an outlier is 0, which ensures a compatibility with other outlier detection algorithms.
- error_norm(comp_cov, norm='frobenius', scaling=True, squared=True)[source]#
Compute the Mean Squared Error between two covariance estimators.
- Parameters:
- comp_covarray-like of shape (n_features, n_features)
The covariance to compare with.
- norm{“frobenius”, “spectral”}, default=”frobenius”
The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error
(comp_cov - self.covariance_).- scalingbool, default=True
If True (default), the squared error norm is divided by n_features. If False, the squared error norm is not rescaled.
- squaredbool, default=True
Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.
- Returns:
- resultfloat
The Mean Squared Error (in the sense of the Frobenius norm) between
selfandcomp_covcovariance estimators.
- fit(X, y=None)[source]#
Fit the EllipticEnvelope model.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Training data.
- yIgnored
Not used, present for API consistency by convention.
- Returns:
- selfobject
Returns the instance itself.
- fit_predict(X, y=None, **kwargs)[source]#
Perform fit on X and returns labels for X.
Returns -1 for outliers and 1 for inliers.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples.
- yIgnored
Not used, present for API consistency by convention.
- **kwargsdict
Arguments to be passed to
fit.Added in version 1.4.
- Returns:
- yndarray of shape (n_samples,)
1 for inliers, -1 for outliers.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- get_precision()[source]#
Getter for the precision matrix.
- Returns:
- precision_array-like of shape (n_features, n_features)
The precision matrix associated to the current covariance object.
- mahalanobis(X)[source]#
Compute the squared Mahalanobis distances of given observations.
For a detailed example of how outliers affects the Mahalanobis distance, see Robust covariance estimation and Mahalanobis distances relevance.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.
- Returns:
- distndarray of shape (n_samples,)
Squared Mahalanobis distances of the observations.
- predict(X)[source]#
Predict labels (1 inlier, -1 outlier) of X according to fitted model.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The data matrix.
- Returns:
- is_inlierndarray of shape (n_samples,)
Returns -1 for anomalies/outliers and +1 for inliers.
- reweight_covariance(data)[source]#
Re-weight raw Minimum Covariance Determinant estimates.
Re-weight observations using Rousseeuw’s method (equivalent to deleting outlying observations from the data set before computing location and covariance estimates) described in [RVDriessen].
Corrects the re-weighted covariance to be consistent at the normal distribution, following [Croux1999].
- Parameters:
- dataarray-like of shape (n_samples, n_features)
The data matrix, with p features and n samples. The data set must be the one which was used to compute the raw estimates.
- Returns:
- location_reweightedndarray of shape (n_features,)
Re-weighted robust location estimate.
- covariance_reweightedndarray of shape (n_features, n_features)
Re-weighted robust covariance estimate.
- support_reweightedndarray of shape (n_samples,), dtype=bool
A mask of the observations that have been used to compute the re-weighted robust location and covariance estimates.
References
[RVDriessen]A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
[Croux1999]Influence Function and Efficiency of the Minimum Covariance Determinant Scatter Matrix Estimator, 1999, Journal of Multivariate Analysis, Volume 71, Issue 2, Pages 161-190
- score(X, y, sample_weight=None)[source]#
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True labels for X.
- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
Mean accuracy of self.predict(X) w.r.t. y.
- score_samples(X)[source]#
Compute the negative Mahalanobis distances.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The data matrix.
- Returns:
- negative_mahal_distancesarray-like of shape (n_samples,)
Opposite of the Mahalanobis distances.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
Gallery examples#
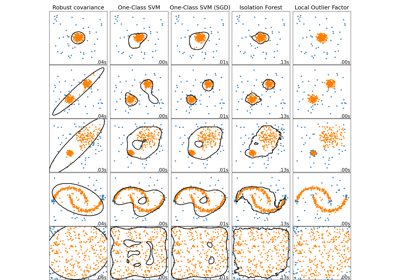
Comparing anomaly detection algorithms for outlier detection on toy datasets