Note

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

Multi-class AdaBoosted Decision Trees#

This example shows how boosting can improve the prediction accuracy on a multi-label classification problem. It reproduces a similar experiment as depicted by Figure 1 in Zhu et al [1].

The core principle of AdaBoost (Adaptive Boosting) is to fit a sequence of weak learners (e.g. Decision Trees) on repeatedly re-sampled versions of the data. Each sample carries a weight that is adjusted after each training step, such that misclassified samples will be assigned higher weights. The re-sampling process with replacement takes into account the weights assigned to each sample. Samples with higher weights have a greater chance of being selected multiple times in the new data set, while samples with lower weights are less likely to be selected. This ensures that subsequent iterations of the algorithm focus on the difficult-to-classify samples.

References

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Creating the dataset#

The classification dataset is constructed by taking a ten-dimensional standard normal distribution (\(x\) in \(R^{10}\)) and defining three classes separated by nested concentric ten-dimensional spheres such that roughly equal numbers of samples are in each class (quantiles of the \(\chi^2\) distribution).

from sklearn.datasets import make_gaussian_quantiles

X, y = make_gaussian_quantiles(
    n_samples=2_000, n_features=10, n_classes=3, random_state=1
)

We split the dataset into 2 sets: 70 percent of the samples are used for training and the remaining 30 percent for testing.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=0.7, random_state=42
)

Training the `AdaBoostClassifier`#

We train the AdaBoostClassifier. The estimator utilizes boosting to improve the classification accuracy. Boosting is a method designed to train weak learners (i.e. estimator) that learn from their predecessor’s mistakes.

Here, we define the weak learner as a DecisionTreeClassifier and set the maximum number of leaves to 8. In a real setting, this parameter should be tuned. We set it to a rather low value to limit the runtime of the example.

The SAMME algorithm build into the AdaBoostClassifier then uses the correct or incorrect predictions made be the current weak learner to update the sample weights used for training the consecutive weak learners. Also, the weight of the weak learner itself is calculated based on its accuracy in classifying the training examples. The weight of the weak learner determines its influence on the final ensemble prediction.

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier

weak_learner = DecisionTreeClassifier(max_leaf_nodes=8)
n_estimators = 300

adaboost_clf = AdaBoostClassifier(
    estimator=weak_learner,
    n_estimators=n_estimators,
    random_state=42,
).fit(X_train, y_train)

Analysis#

Convergence of the `AdaBoostClassifier`#

To demonstrate the effectiveness of boosting in improving accuracy, we evaluate the misclassification error of the boosted trees in comparison to two baseline scores. The first baseline score is the misclassification_error obtained from a single weak-learner (i.e. DecisionTreeClassifier), which serves as a reference point. The second baseline score is obtained from the DummyClassifier, which predicts the most prevalent class in a dataset.

from sklearn.dummy import DummyClassifier
from sklearn.metrics import accuracy_score

dummy_clf = DummyClassifier()


def misclassification_error(y_true, y_pred):
    return 1 - accuracy_score(y_true, y_pred)


weak_learners_misclassification_error = misclassification_error(
    y_test, weak_learner.fit(X_train, y_train).predict(X_test)
)

dummy_classifiers_misclassification_error = misclassification_error(
    y_test, dummy_clf.fit(X_train, y_train).predict(X_test)
)

print(
    "DecisionTreeClassifier's misclassification_error: "
    f"{weak_learners_misclassification_error:.3f}"
)
print(
    "DummyClassifier's misclassification_error: "
    f"{dummy_classifiers_misclassification_error:.3f}"
)

DecisionTreeClassifier's misclassification_error: 0.475
DummyClassifier's misclassification_error: 0.692

After training the DecisionTreeClassifier model, the achieved error surpasses the expected value that would have been obtained by guessing the most frequent class label, as the DummyClassifier does.

Now, we calculate the misclassification_error, i.e. 1 - accuracy, of the additive model (DecisionTreeClassifier) at each boosting iteration on the test set to assess its performance.

We use staged_predict that makes as many iterations as the number of fitted estimator (i.e. corresponding to n_estimators). At iteration n, the predictions of AdaBoost only use the n first weak learners. We compare these predictions with the true predictions y_test and we, therefore, conclude on the benefit (or not) of adding a new weak learner into the chain.

We plot the misclassification error for the different stages:

import matplotlib.pyplot as plt
import pandas as pd

boosting_errors = pd.DataFrame(
    {
        "Number of trees": range(1, n_estimators + 1),
        "AdaBoost": [
            misclassification_error(y_test, y_pred)
            for y_pred in adaboost_clf.staged_predict(X_test)
        ],
    }
).set_index("Number of trees")
ax = boosting_errors.plot()
ax.set_ylabel("Misclassification error on test set")
ax.set_title("Convergence of AdaBoost algorithm")

plt.plot(
    [boosting_errors.index.min(), boosting_errors.index.max()],
    [weak_learners_misclassification_error, weak_learners_misclassification_error],
    color="tab:orange",
    linestyle="dashed",
)
plt.plot(
    [boosting_errors.index.min(), boosting_errors.index.max()],
    [
        dummy_classifiers_misclassification_error,
        dummy_classifiers_misclassification_error,
    ],
    color="c",
    linestyle="dotted",
)
plt.legend(["AdaBoost", "DecisionTreeClassifier", "DummyClassifier"], loc=1)
plt.show()

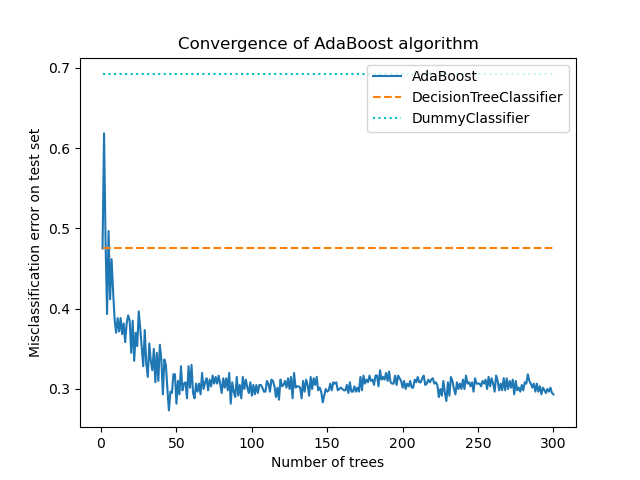
The plot shows the missclassification error on the test set after each boosting iteration. We see that the error of the boosted trees converges to an error of around 0.3 after 50 iterations, indicating a significantly higher accuracy compared to a single tree, as illustrated by the dashed line in the plot.

The misclassification error jitters because the SAMME algorithm uses the discrete outputs of the weak learners to train the boosted model.

The convergence of AdaBoostClassifier is mainly influenced by the learning rate (i.e. learning_rate), the number of weak learners used (n_estimators), and the expressivity of the weak learners (e.g. max_leaf_nodes).

Errors and weights of the Weak Learners#

As previously mentioned, AdaBoost is a forward stagewise additive model. We now focus on understanding the relationship between the attributed weights of the weak learners and their statistical performance.

We use the fitted AdaBoostClassifier’s attributes estimator_errors_ and estimator_weights_ to investigate this link.

weak_learners_info = pd.DataFrame(
    {
        "Number of trees": range(1, n_estimators + 1),
        "Errors": adaboost_clf.estimator_errors_,
        "Weights": adaboost_clf.estimator_weights_,
    }
).set_index("Number of trees")

axs = weak_learners_info.plot(
    subplots=True, layout=(1, 2), figsize=(10, 4), legend=False, color="tab:blue"
)
axs[0, 0].set_ylabel("Train error")
axs[0, 0].set_title("Weak learner's training error")
axs[0, 1].set_ylabel("Weight")
axs[0, 1].set_title("Weak learner's weight")
fig = axs[0, 0].get_figure()
fig.suptitle("Weak learner's errors and weights for the AdaBoostClassifier")
fig.tight_layout()

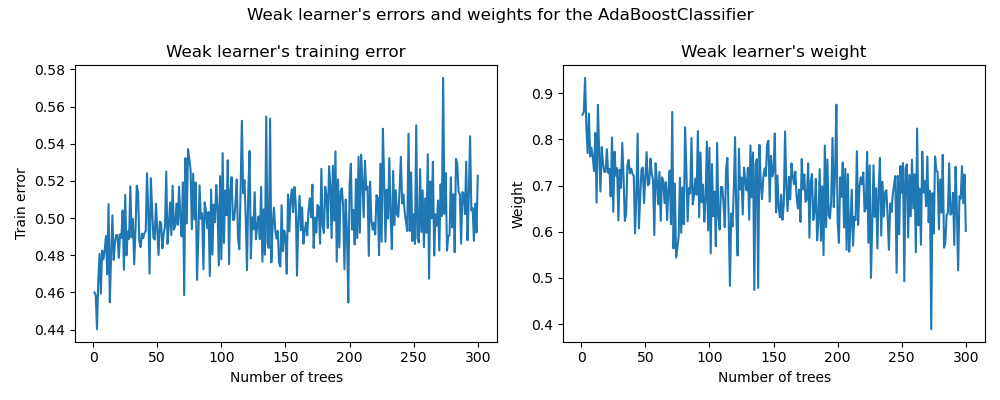
Weak learner's errors and weights for the AdaBoostClassifier, Weak learner's training error, Weak learner's weight

On the left plot, we show the weighted error of each weak learner on the reweighted training set at each boosting iteration. On the right plot, we show the weights associated with each weak learner later used to make the predictions of the final additive model.

We see that the error of the weak learner is the inverse of the weights. It means that our additive model will trust more a weak learner that makes smaller errors (on the training set) by increasing its impact on the final decision. Indeed, this exactly is the formulation of updating the base estimators’ weights after each iteration in AdaBoost.

Another interesting observation boils down to the fact that the first weak learners of the model make fewer errors than later weak learners of the boosting chain.

The intuition behind this observation is the following: due to the sample reweighting, later classifiers are forced to try to classify more difficult or noisy samples and to ignore already well classified samples. Therefore, the overall error on the training set will increase. That’s why the weak learner’s weights are built to counter-balance the worse performing weak learners.

Total running time of the script: (0 minutes 4.553 seconds)