Note

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

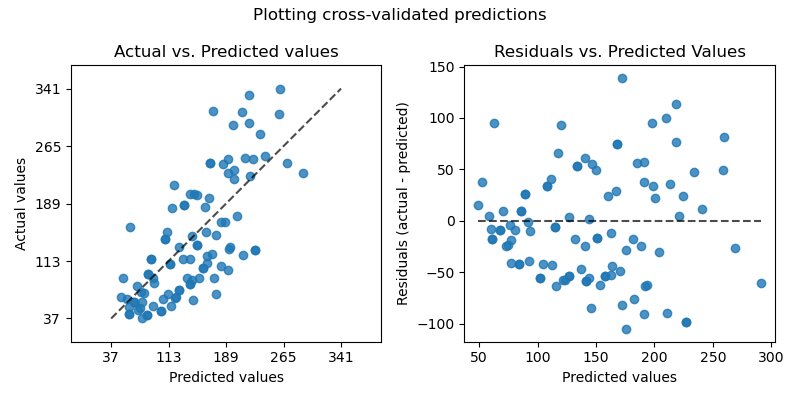
Plotting Cross-Validated Predictions#

This example shows how to use cross_val_predict together with PredictionErrorDisplay to visualize prediction errors.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

We will load the diabetes dataset and create an instance of a linear regression model.

from sklearn.datasets import load_diabetes
from sklearn.linear_model import LinearRegression

X, y = load_diabetes(return_X_y=True)
lr = LinearRegression()

cross_val_predict returns an array of the same size of y where each entry is a prediction obtained by cross validation.

from sklearn.model_selection import cross_val_predict

y_pred = cross_val_predict(lr, X, y, cv=10)

Since cv=10, it means that we trained 10 models and each model was used to predict on one of the 10 folds. We can now use the PredictionErrorDisplay to visualize the prediction errors.

On the left axis, we plot the observed values \(y\) vs. the predicted values \(\hat{y}\) given by the models. On the right axis, we plot the residuals (i.e. the difference between the observed values and the predicted values) vs. the predicted values.

import matplotlib.pyplot as plt

from sklearn.metrics import PredictionErrorDisplay

fig, axs = plt.subplots(ncols=2, figsize=(8, 4))
PredictionErrorDisplay.from_predictions(
    y,
    y_pred=y_pred,
    kind="actual_vs_predicted",
    subsample=100,
    ax=axs[0],
    random_state=0,
)
axs[0].set_title("Actual vs. Predicted values")
PredictionErrorDisplay.from_predictions(
    y,
    y_pred=y_pred,
    kind="residual_vs_predicted",
    subsample=100,
    ax=axs[1],
    random_state=0,
)
axs[1].set_title("Residuals vs. Predicted Values")
fig.suptitle("Plotting cross-validated predictions")
plt.tight_layout()
plt.show()

Plotting cross-validated predictions, Actual vs. Predicted values, Residuals vs. Predicted Values

It is important to note that we used cross_val_predict for visualization purpose only in this example.

It would be problematic to quantitatively assess the model performance by computing a single performance metric from the concatenated predictions returned by cross_val_predict when the different CV folds vary by size and distributions.

It is recommended to compute per-fold performance metrics using: cross_val_score or cross_validate instead.

Total running time of the script: (0 minutes 0.207 seconds)