Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder.
Incremental PCA#
Incremental principal component analysis (IPCA) is typically used as a replacement for principal component analysis (PCA) when the dataset to be decomposed is too large to fit in memory. IPCA builds a low-rank approximation for the input data using an amount of memory which is independent of the number of input data samples. It is still dependent on the input data features, but changing the batch size allows for control of memory usage.
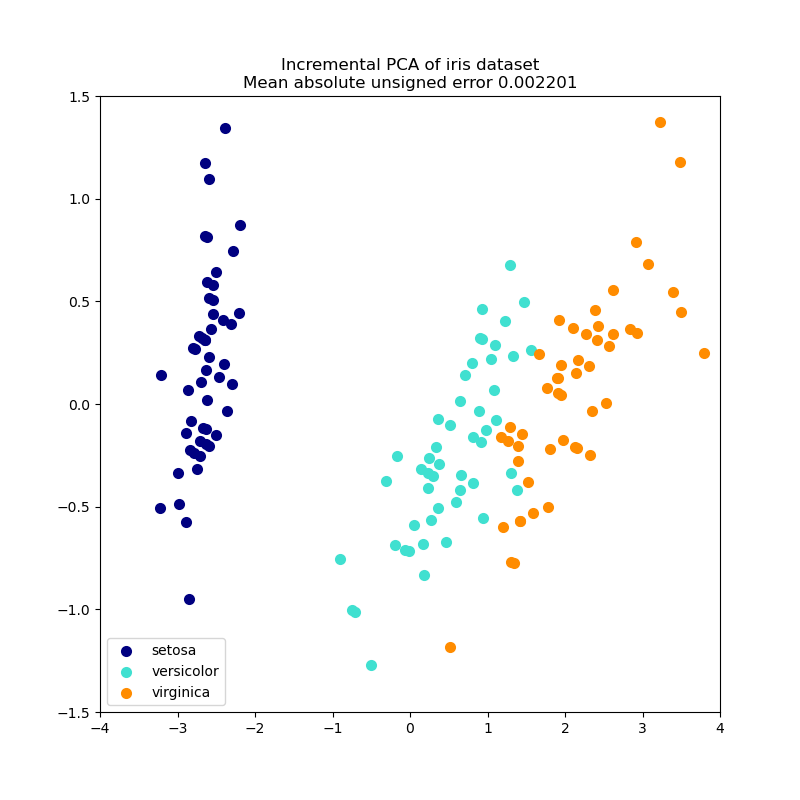
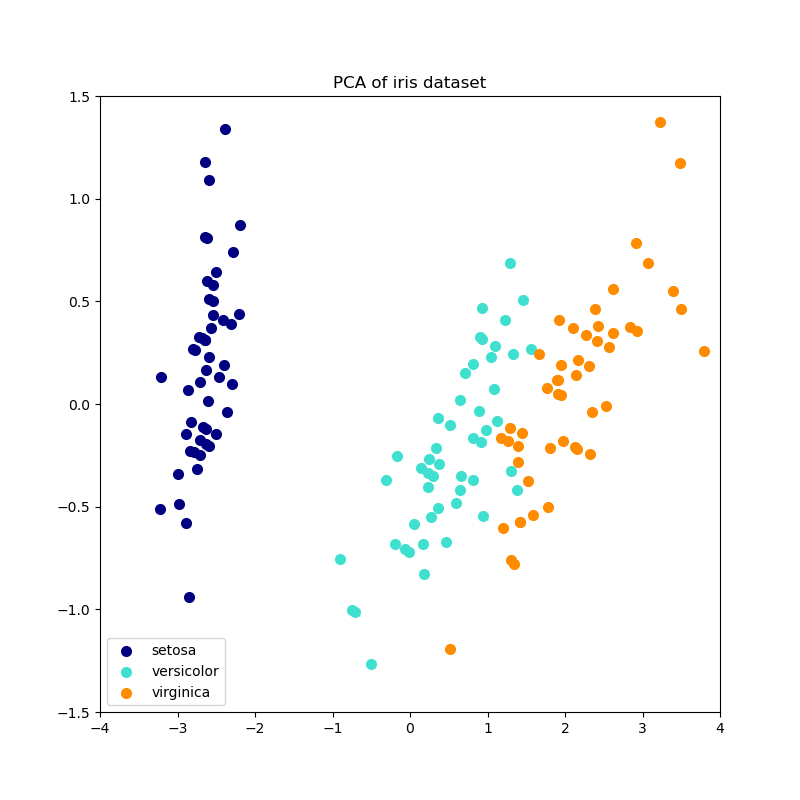
This example serves as a visual check that IPCA is able to find a similar projection of the data to PCA (to a sign flip), while only processing a few samples at a time. This can be considered a “toy example”, as IPCA is intended for large datasets which do not fit in main memory, requiring incremental approaches.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA, IncrementalPCA
iris = load_iris()
X = iris.data
y = iris.target
n_components = 2
ipca = IncrementalPCA(n_components=n_components, batch_size=10)
X_ipca = ipca.fit_transform(X)
pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)
colors = ["navy", "turquoise", "darkorange"]
for X_transformed, title in [(X_ipca, "Incremental PCA"), (X_pca, "PCA")]:
plt.figure(figsize=(8, 8))
for color, i, target_name in zip(colors, [0, 1, 2], iris.target_names):
plt.scatter(
X_transformed[y == i, 0],
X_transformed[y == i, 1],
color=color,
lw=2,
label=target_name,
)
if "Incremental" in title:
err = np.abs(np.abs(X_pca) - np.abs(X_ipca)).mean()
plt.title(title + " of iris dataset\nMean absolute unsigned error %.6f" % err)
else:
plt.title(title + " of iris dataset")
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.axis([-4, 4, -1.5, 1.5])
plt.show()
Total running time of the script: (0 minutes 0.183 seconds)
Related examples
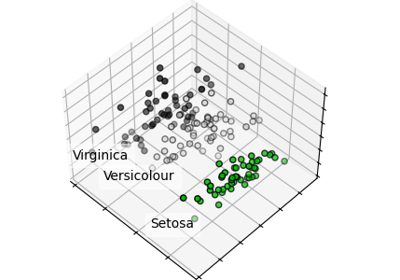
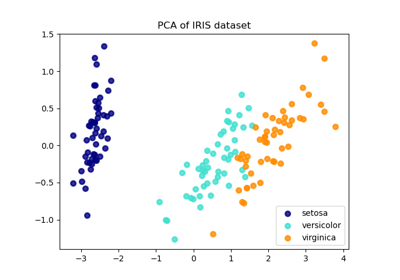
Principal Component Analysis (PCA) on Iris Dataset
Comparison of LDA and PCA 2D projection of Iris dataset
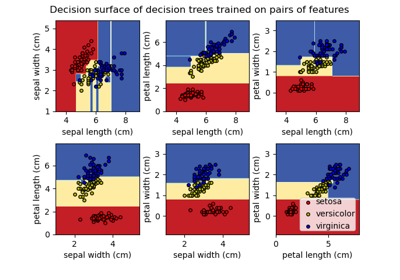
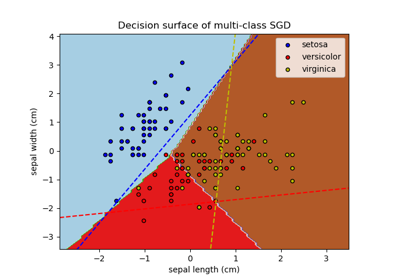
Plot the decision surface of decision trees trained on the iris dataset