Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder.
Compare the effect of different scalers on data with outliers#
Feature 0 (median income in a block) and feature 5 (average house occupancy) of the California Housing dataset have very different scales and contain some very large outliers. These two characteristics lead to difficulties to visualize the data and, more importantly, they can degrade the predictive performance of many machine learning algorithms. Unscaled data can also slow down or even prevent the convergence of many gradient-based estimators.
Indeed many estimators are designed with the assumption that each feature takes values close to zero or more importantly that all features vary on comparable scales. In particular, metric-based and gradient-based estimators often assume approximately standardized data (centered features with unit variances). A notable exception are decision tree-based estimators that are robust to arbitrary scaling of the data.
This example uses different scalers, transformers, and normalizers to bring the data within a pre-defined range.
Scalers are linear (or more precisely affine) transformers and differ from each other in the way they estimate the parameters used to shift and scale each feature.
QuantileTransformer provides non-linear
transformations in which distances
between marginal outliers and inliers are shrunk.
PowerTransformer provides
non-linear transformations in which data is mapped to a normal distribution to
stabilize variance and minimize skewness.
Unlike the previous transformations, normalization refers to a per sample transformation instead of a per feature transformation.
The following code is a bit verbose, feel free to jump directly to the analysis of the results.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib as mpl
import numpy as np
from matplotlib import cm
from matplotlib import pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import (
MaxAbsScaler,
MinMaxScaler,
Normalizer,
PowerTransformer,
QuantileTransformer,
RobustScaler,
StandardScaler,
minmax_scale,
)
dataset = fetch_california_housing()
X_full, y_full = dataset.data, dataset.target
feature_names = dataset.feature_names
feature_mapping = {
"MedInc": "Median income in block",
"HouseAge": "Median house age in block",
"AveRooms": "Average number of rooms",
"AveBedrms": "Average number of bedrooms",
"Population": "Block population",
"AveOccup": "Average house occupancy",
"Latitude": "House block latitude",
"Longitude": "House block longitude",
}
# Take only 2 features to make visualization easier
# Feature MedInc has a long tail distribution.
# Feature AveOccup has a few but very large outliers.
features = ["MedInc", "AveOccup"]
features_idx = [feature_names.index(feature) for feature in features]
X = X_full[:, features_idx]
distributions = [
("Unscaled data", X),
("Data after standard scaling", StandardScaler().fit_transform(X)),
("Data after min-max scaling", MinMaxScaler().fit_transform(X)),
("Data after max-abs scaling", MaxAbsScaler().fit_transform(X)),
(
"Data after robust scaling",
RobustScaler(quantile_range=(25, 75)).fit_transform(X),
),
(
"Data after power transformation (Yeo-Johnson)",
PowerTransformer(method="yeo-johnson").fit_transform(X),
),
(
"Data after power transformation (Box-Cox)",
PowerTransformer(method="box-cox").fit_transform(X),
),
(
"Data after quantile transformation (uniform pdf)",
QuantileTransformer(
output_distribution="uniform", random_state=42
).fit_transform(X),
),
(
"Data after quantile transformation (gaussian pdf)",
QuantileTransformer(
output_distribution="normal", random_state=42
).fit_transform(X),
),
("Data after sample-wise L2 normalizing", Normalizer().fit_transform(X)),
]
# scale the output between 0 and 1 for the colorbar
y = minmax_scale(y_full)
# plasma does not exist in matplotlib < 1.5
cmap = getattr(cm, "plasma_r", cm.hot_r)
def create_axes(title, figsize=(16, 6)):
fig = plt.figure(figsize=figsize)
fig.suptitle(title)
# define the axis for the first plot
left, width = 0.1, 0.22
bottom, height = 0.1, 0.7
bottom_h = height + 0.15
left_h = left + width + 0.02
rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.1]
rect_histy = [left_h, bottom, 0.05, height]
ax_scatter = plt.axes(rect_scatter)
ax_histx = plt.axes(rect_histx)
ax_histy = plt.axes(rect_histy)
# define the axis for the zoomed-in plot
left = width + left + 0.2
left_h = left + width + 0.02
rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.1]
rect_histy = [left_h, bottom, 0.05, height]
ax_scatter_zoom = plt.axes(rect_scatter)
ax_histx_zoom = plt.axes(rect_histx)
ax_histy_zoom = plt.axes(rect_histy)
# define the axis for the colorbar
left, width = width + left + 0.13, 0.01
rect_colorbar = [left, bottom, width, height]
ax_colorbar = plt.axes(rect_colorbar)
return (
(ax_scatter, ax_histy, ax_histx),
(ax_scatter_zoom, ax_histy_zoom, ax_histx_zoom),
ax_colorbar,
)
def plot_distribution(axes, X, y, hist_nbins=50, title="", x0_label="", x1_label=""):
ax, hist_X1, hist_X0 = axes
ax.set_title(title)
ax.set_xlabel(x0_label)
ax.set_ylabel(x1_label)
# The scatter plot
colors = cmap(y)
ax.scatter(X[:, 0], X[:, 1], alpha=0.5, marker="o", s=5, lw=0, c=colors)
# Removing the top and the right spine for aesthetics
# make nice axis layout
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
ax.spines["left"].set_position(("outward", 10))
ax.spines["bottom"].set_position(("outward", 10))
# Histogram for axis X1 (feature 5)
hist_X1.set_ylim(ax.get_ylim())
hist_X1.hist(
X[:, 1], bins=hist_nbins, orientation="horizontal", color="grey", ec="grey"
)
hist_X1.axis("off")
# Histogram for axis X0 (feature 0)
hist_X0.set_xlim(ax.get_xlim())
hist_X0.hist(
X[:, 0], bins=hist_nbins, orientation="vertical", color="grey", ec="grey"
)
hist_X0.axis("off")
Two plots will be shown for each scaler/normalizer/transformer. The left figure will show a scatter plot of the full data set while the right figure will exclude the extreme values considering only 99 % of the data set, excluding marginal outliers. In addition, the marginal distributions for each feature will be shown on the sides of the scatter plot.
def make_plot(item_idx):
title, X = distributions[item_idx]
ax_zoom_out, ax_zoom_in, ax_colorbar = create_axes(title)
axarr = (ax_zoom_out, ax_zoom_in)
plot_distribution(
axarr[0],
X,
y,
hist_nbins=200,
x0_label=feature_mapping[features[0]],
x1_label=feature_mapping[features[1]],
title="Full data",
)
# zoom-in
zoom_in_percentile_range = (0, 99)
cutoffs_X0 = np.percentile(X[:, 0], zoom_in_percentile_range)
cutoffs_X1 = np.percentile(X[:, 1], zoom_in_percentile_range)
non_outliers_mask = np.all(X > [cutoffs_X0[0], cutoffs_X1[0]], axis=1) & np.all(
X < [cutoffs_X0[1], cutoffs_X1[1]], axis=1
)
plot_distribution(
axarr[1],
X[non_outliers_mask],
y[non_outliers_mask],
hist_nbins=50,
x0_label=feature_mapping[features[0]],
x1_label=feature_mapping[features[1]],
title="Zoom-in",
)
norm = mpl.colors.Normalize(y_full.min(), y_full.max())
mpl.colorbar.ColorbarBase(
ax_colorbar,
cmap=cmap,
norm=norm,
orientation="vertical",
label="Color mapping for values of y",
)
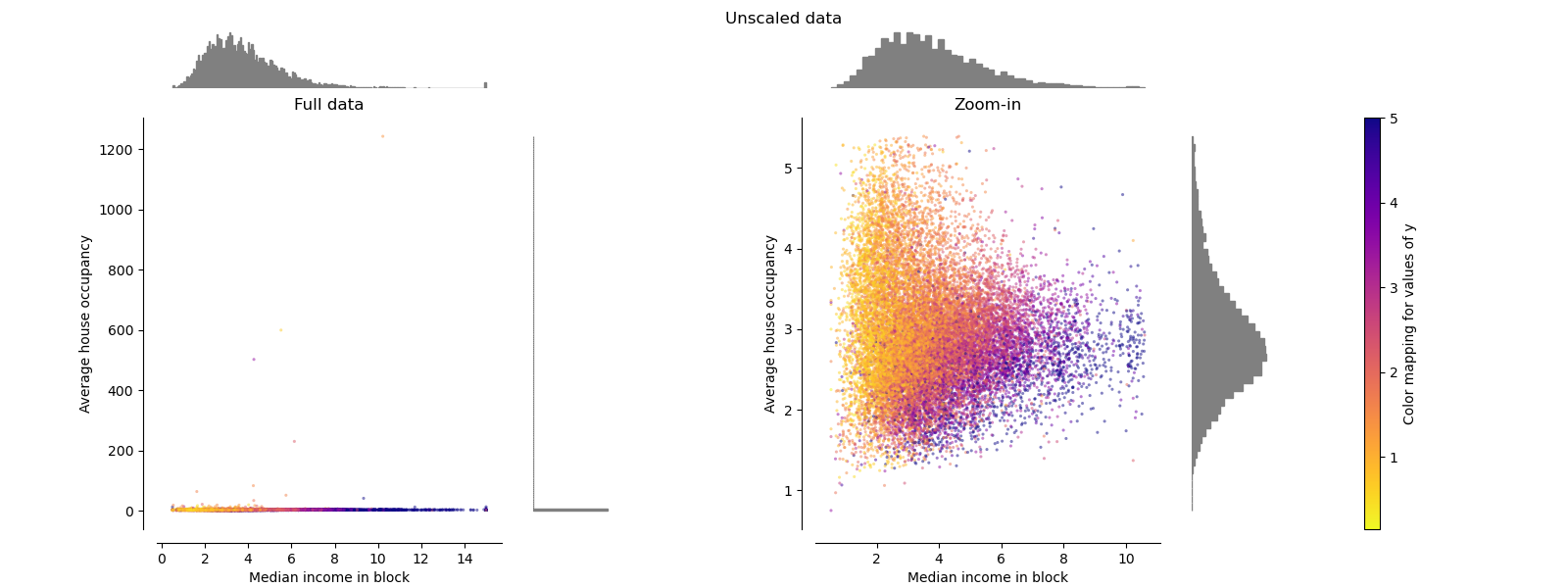
Original data#
Each transformation is plotted showing two transformed features, with the left plot showing the entire dataset, and the right zoomed-in to show the dataset without the marginal outliers. A large majority of the samples are compacted to a specific range, [0, 10] for the median income and [0, 6] for the average house occupancy. Note that there are some marginal outliers (some blocks have average occupancy of more than 1200). Therefore, a specific pre-processing can be very beneficial depending of the application. In the following, we present some insights and behaviors of those pre-processing methods in the presence of marginal outliers.
make_plot(0)
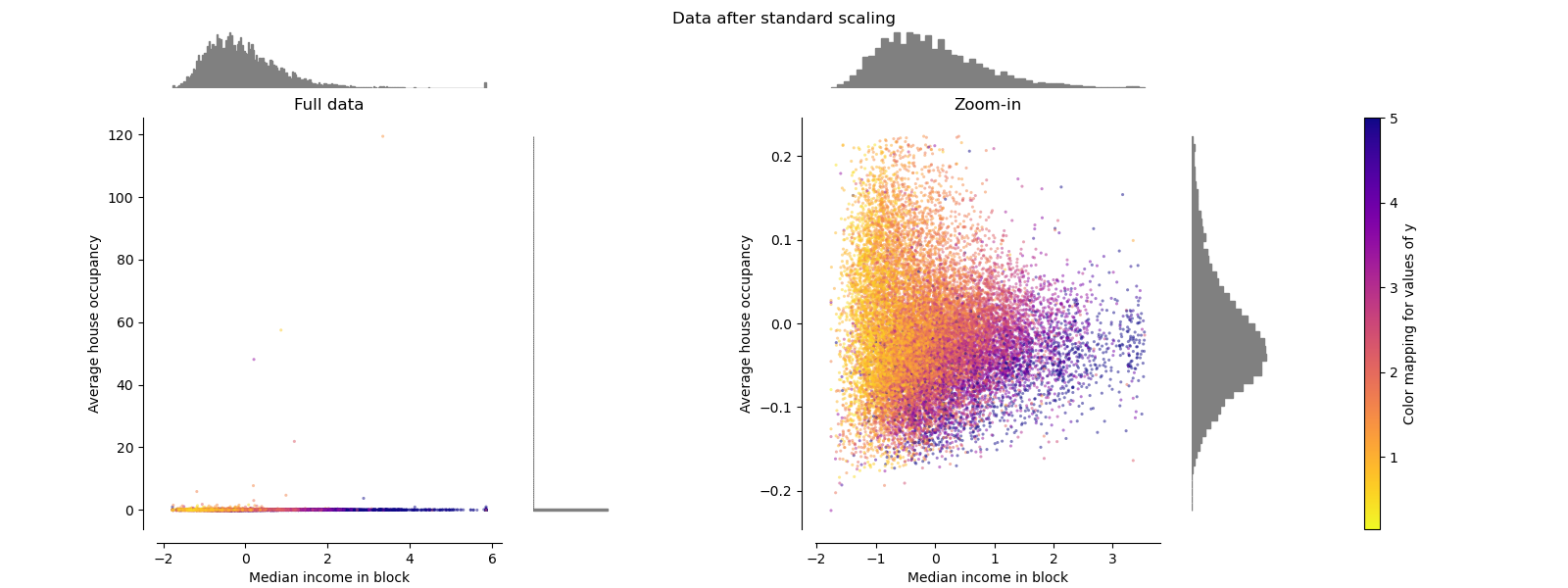
StandardScaler#
StandardScaler removes the mean and scales
the data to unit variance. The scaling shrinks the range of the feature
values as shown in the left figure below.
However, the outliers have an influence when computing the empirical mean and
standard deviation. Note in particular that because the outliers on each
feature have different magnitudes, the spread of the transformed data on
each feature is very different: most of the data lie in the [-2, 4] range for
the transformed median income feature while the same data is squeezed in the
smaller [-0.2, 0.2] range for the transformed average house occupancy.
StandardScaler therefore cannot guarantee
balanced feature scales in the
presence of outliers.
make_plot(1)
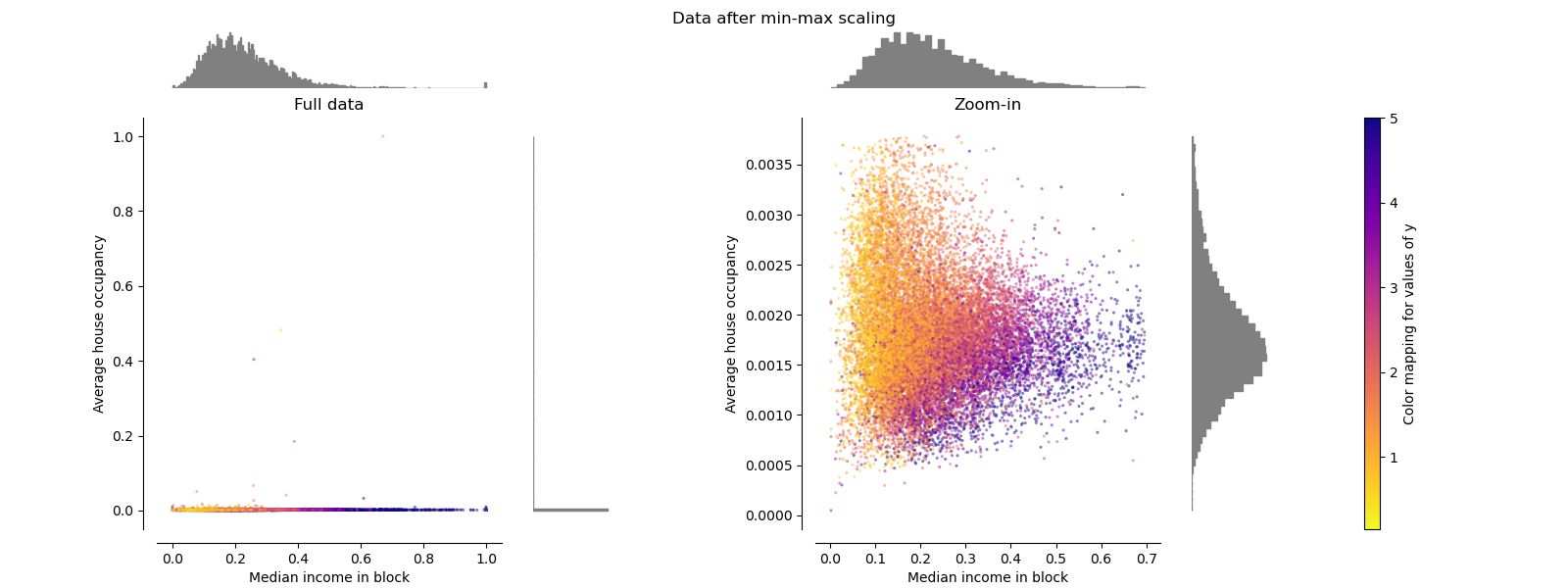
MinMaxScaler#
MinMaxScaler rescales the data set such that
all feature values are in
the range [0, 1] as shown in the right panel below. However, this scaling
compresses all inliers into the narrow range [0, 0.005] for the transformed
average house occupancy.
Both StandardScaler and
MinMaxScaler are very sensitive to the
presence of outliers.
make_plot(2)
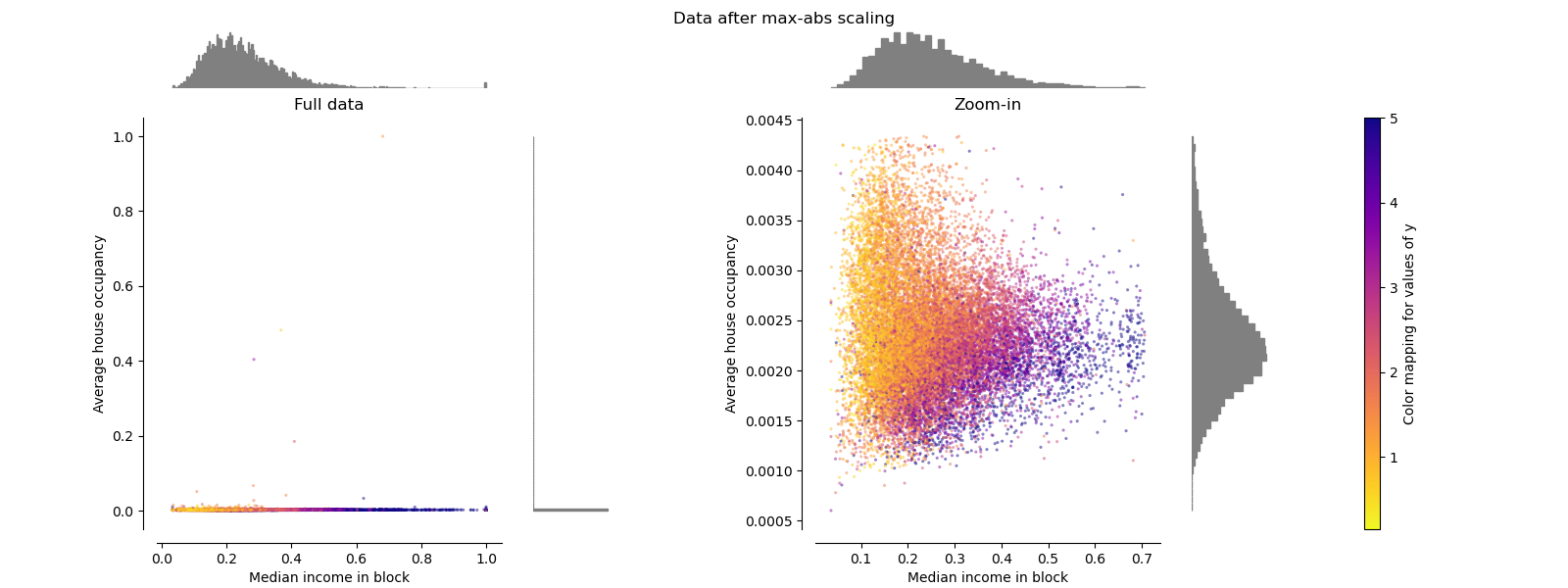
MaxAbsScaler#
MaxAbsScaler is similar to
MinMaxScaler except that the
values are mapped across several ranges depending on whether negative
OR positive values are present. If only positive values are present, the
range is [0, 1]. If only negative values are present, the range is [-1, 0].
If both negative and positive values are present, the range is [-1, 1].
On positive only data, both MinMaxScaler
and MaxAbsScaler behave similarly.
MaxAbsScaler therefore also suffers from
the presence of large outliers.
make_plot(3)
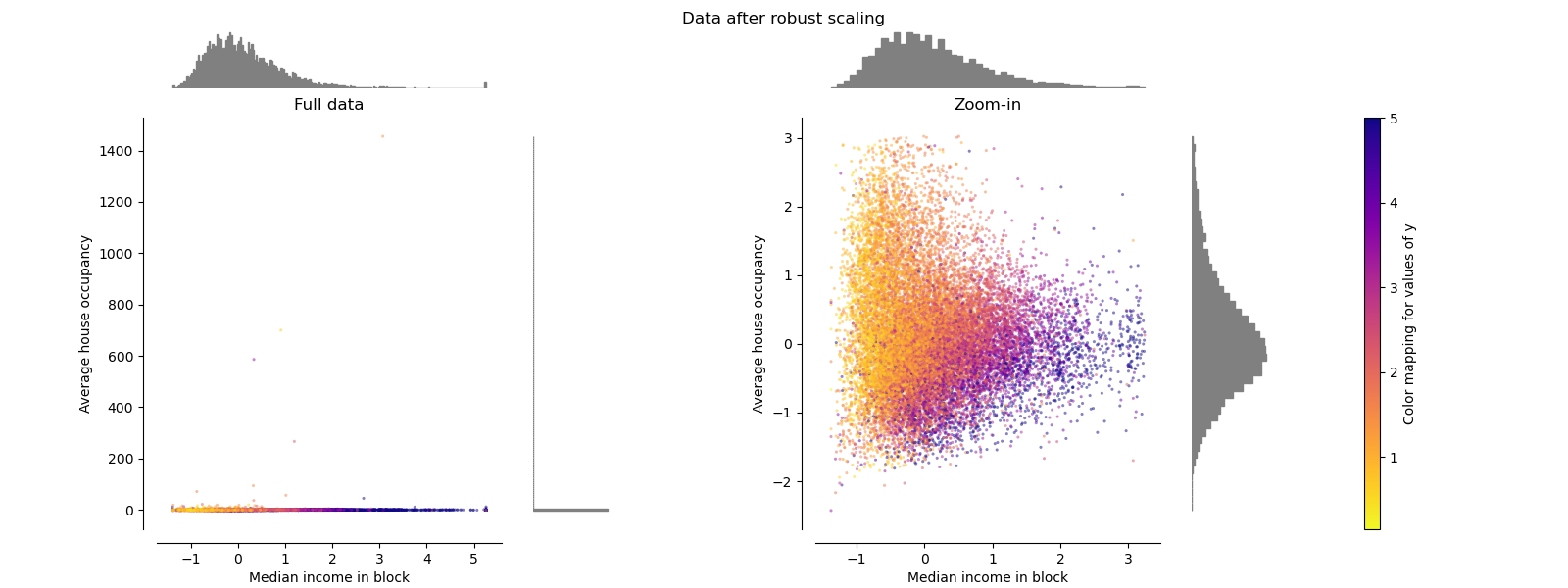
RobustScaler#
Unlike the previous scalers, the centering and scaling statistics of
RobustScaler
are based on percentiles and are therefore not influenced by a small
number of very large marginal outliers. Consequently, the resulting range of
the transformed feature values is larger than for the previous scalers and,
more importantly, are approximately similar: for both features most of the
transformed values lie in a [-2, 3] range as seen in the zoomed-in figure.
Note that the outliers themselves are still present in the transformed data.
If a separate outlier clipping is desirable, a non-linear transformation is
required (see below).
make_plot(4)
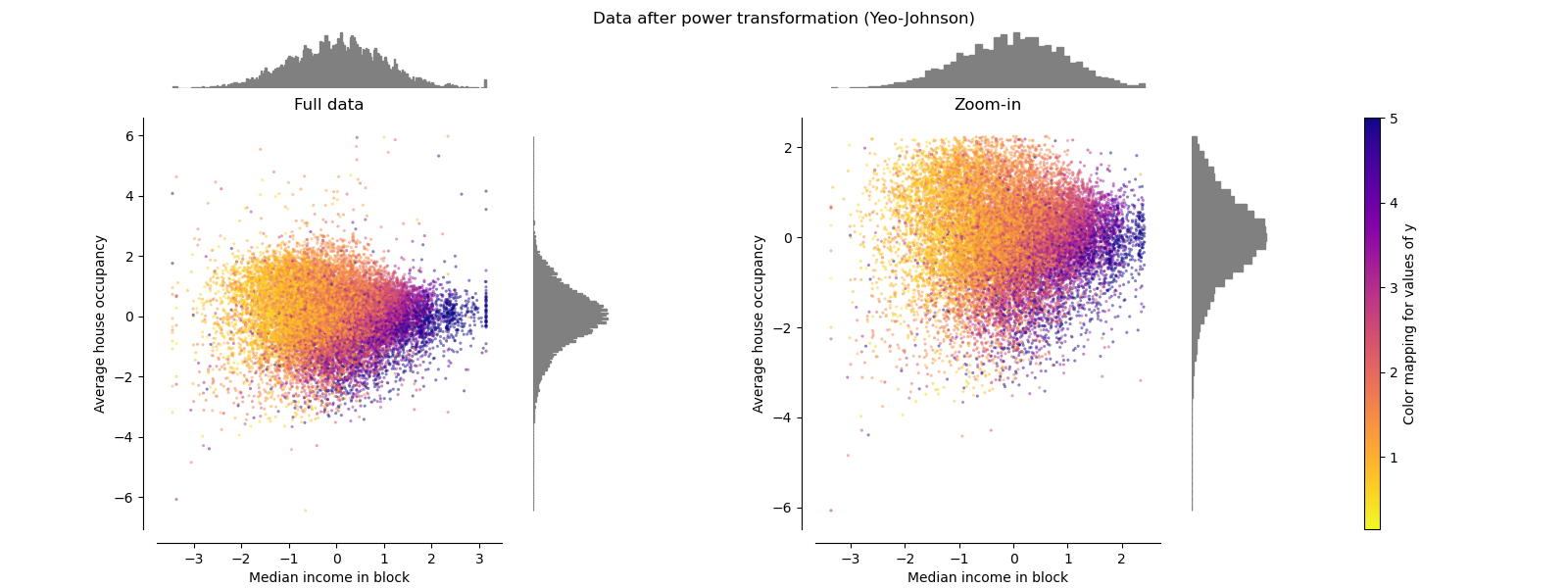
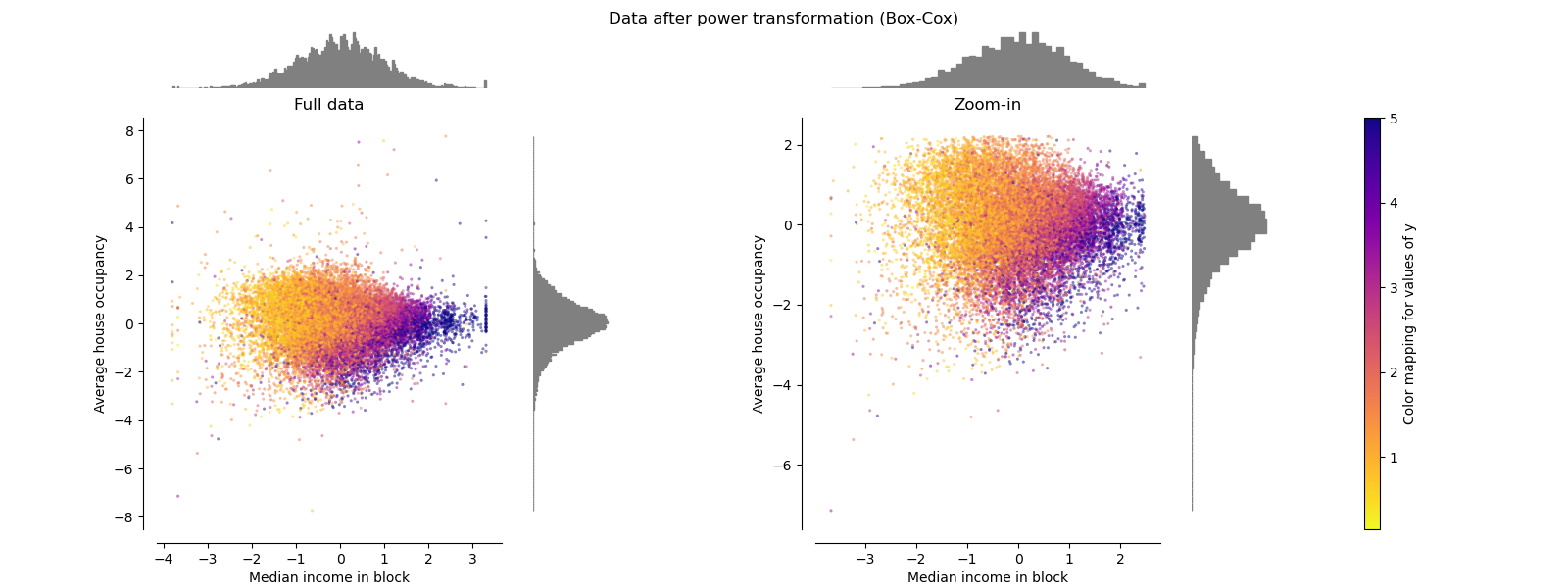
PowerTransformer#
PowerTransformer applies a power
transformation to each feature to make the data more Gaussian-like in order
to stabilize variance and minimize skewness. Currently the Yeo-Johnson
and Box-Cox transforms are supported and the optimal
scaling factor is determined via maximum likelihood estimation in both
methods. By default, PowerTransformer applies
zero-mean, unit variance normalization. Note that
Box-Cox can only be applied to strictly positive data. Income and average
house occupancy happen to be strictly positive, but if negative values are
present the Yeo-Johnson transformed is preferred.
make_plot(5)
make_plot(6)
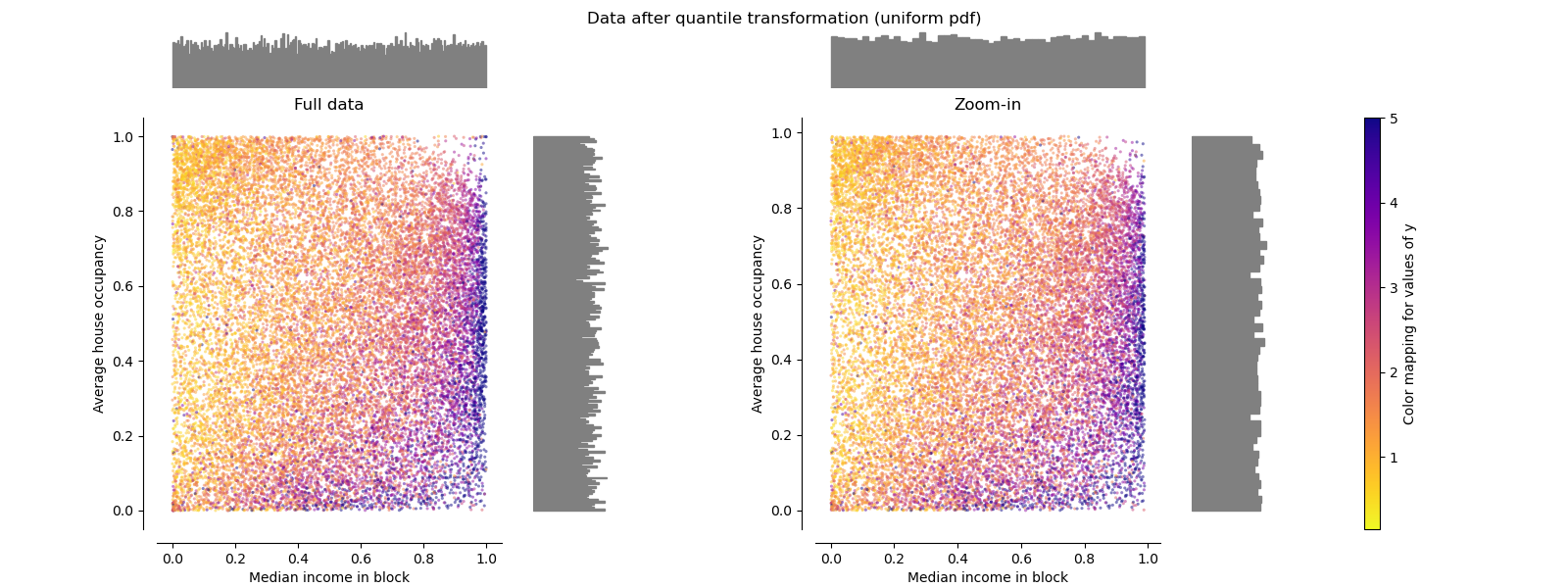
QuantileTransformer (uniform output)#
QuantileTransformer applies a non-linear
transformation such that the
probability density function of each feature will be mapped to a uniform
or Gaussian distribution. In this case, all the data, including outliers,
will be mapped to a uniform distribution with the range [0, 1], making
outliers indistinguishable from inliers.
RobustScaler and
QuantileTransformer are robust to outliers in
the sense that adding or removing outliers in the training set will yield
approximately the same transformation. But contrary to
RobustScaler,
QuantileTransformer will also automatically
collapse any outlier by setting them to the a priori defined range boundaries
(0 and 1). This can result in saturation artifacts for extreme values.
make_plot(7)
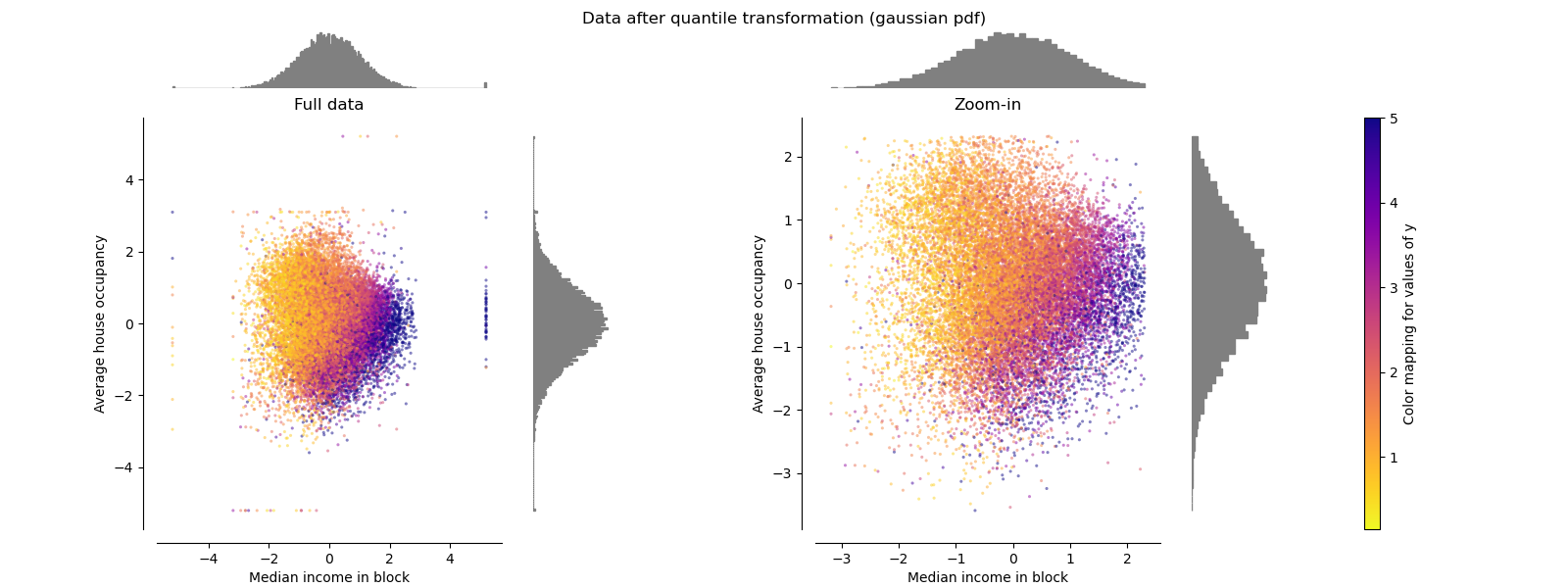
QuantileTransformer (Gaussian output)#
To map to a Gaussian distribution, set the parameter
output_distribution='normal'.
make_plot(8)
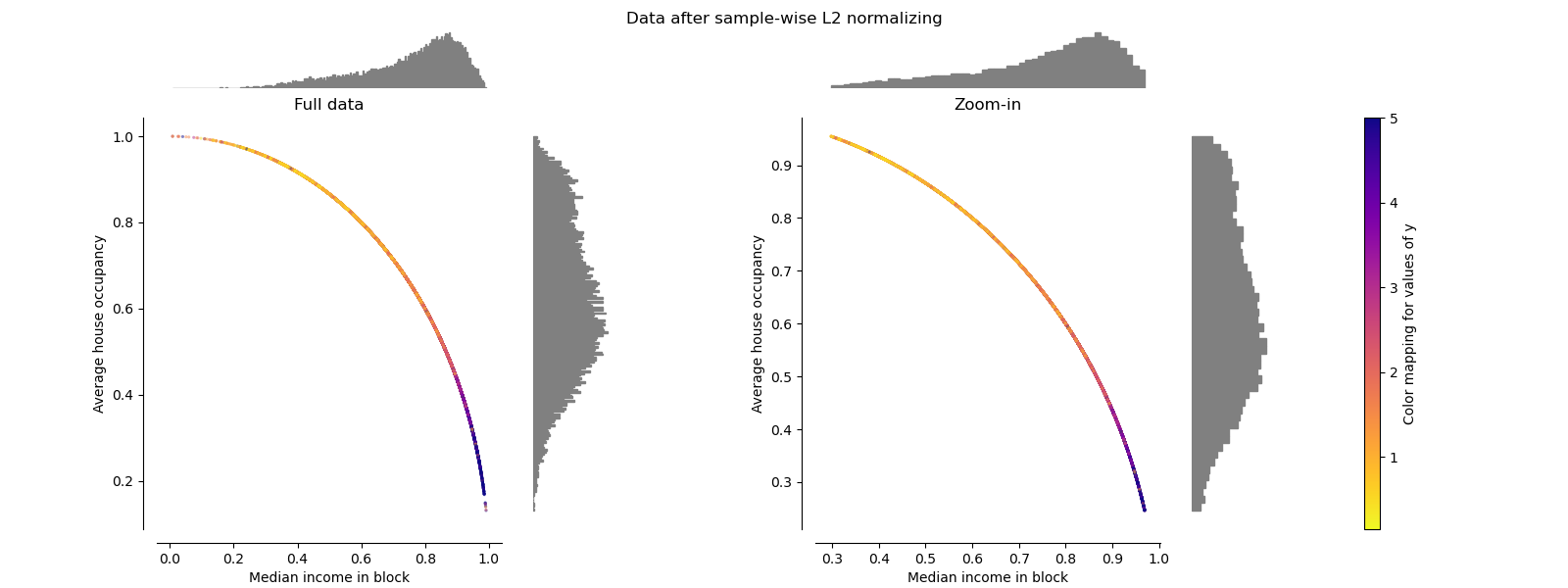
Normalizer#
The Normalizer rescales the vector for each
sample to have unit norm,
independently of the distribution of the samples. It can be seen on both
figures below where all samples are mapped onto the unit circle. In our
example the two selected features have only positive values; therefore the
transformed data only lie in the positive quadrant. This would not be the
case if some original features had a mix of positive and negative values.
make_plot(9)
plt.show()
Total running time of the script: (0 minutes 8.127 seconds)
Related examples