Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder.
IsolationForest example#
An example using IsolationForest for anomaly
detection.
The Isolation Forest is an ensemble of “Isolation Trees” that “isolate” observations by recursive random partitioning, which can be represented by a tree structure. The number of splittings required to isolate a sample is lower for outliers and higher for inliers.
In the present example we demo two ways to visualize the decision boundary of an Isolation Forest trained on a toy dataset.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Data generation#
We generate two clusters (each one containing n_samples) by randomly
sampling the standard normal distribution as returned by
numpy.random.randn. One of them is spherical and the other one is
slightly deformed.
For consistency with the IsolationForest notation,
the inliers (i.e. the gaussian clusters) are assigned a ground truth label 1
whereas the outliers (created with numpy.random.uniform) are assigned
the label -1.
import numpy as np
from sklearn.model_selection import train_test_split
n_samples, n_outliers = 120, 40
rng = np.random.RandomState(0)
covariance = np.array([[0.5, -0.1], [0.7, 0.4]])
cluster_1 = 0.4 * rng.randn(n_samples, 2) @ covariance + np.array([2, 2]) # general
cluster_2 = 0.3 * rng.randn(n_samples, 2) + np.array([-2, -2]) # spherical
outliers = rng.uniform(low=-4, high=4, size=(n_outliers, 2))
X = np.concatenate([cluster_1, cluster_2, outliers])
y = np.concatenate(
[np.ones((2 * n_samples), dtype=int), -np.ones((n_outliers), dtype=int)]
)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
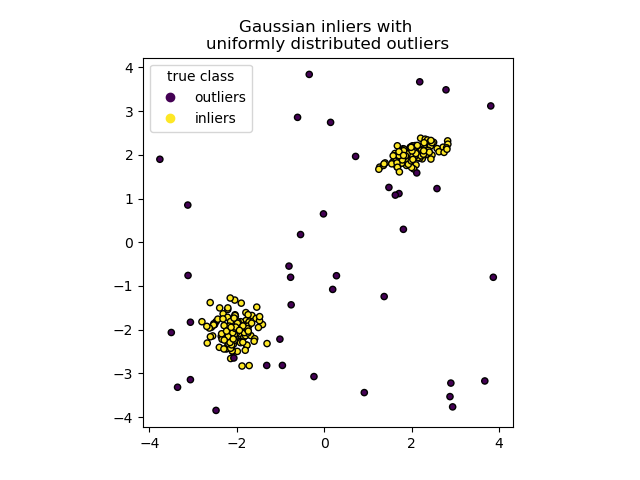
We can visualize the resulting clusters:
import matplotlib.pyplot as plt
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor="k")
handles, labels = scatter.legend_elements()
plt.axis("square")
plt.legend(handles=handles, labels=["outliers", "inliers"], title="true class")
plt.title("Gaussian inliers with \nuniformly distributed outliers")
plt.show()
Training of the model#
from sklearn.ensemble import IsolationForest
clf = IsolationForest(max_samples=100, random_state=0)
clf.fit(X_train)
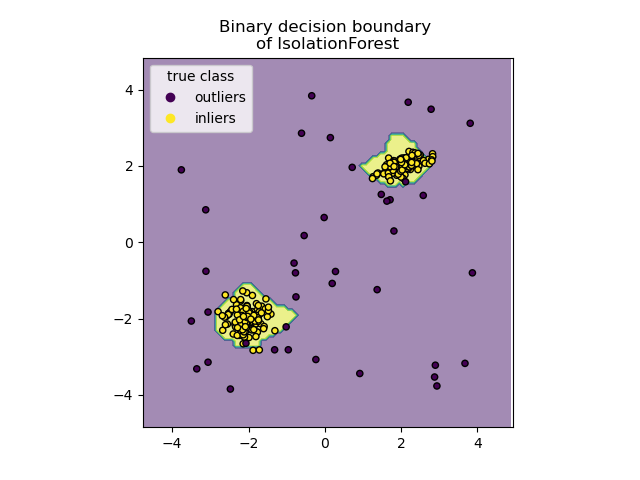
Plot discrete decision boundary#
We use the class DecisionBoundaryDisplay to
visualize a discrete decision boundary. The background color represents
whether a sample in that given area is predicted to be an outlier
or not. The scatter plot displays the true labels.
import matplotlib.pyplot as plt
from sklearn.inspection import DecisionBoundaryDisplay
disp = DecisionBoundaryDisplay.from_estimator(
clf,
X,
response_method="predict",
alpha=0.5,
)
disp.ax_.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor="k")
disp.ax_.set_title("Binary decision boundary \nof IsolationForest")
plt.axis("square")
plt.legend(handles=handles, labels=["outliers", "inliers"], title="true class")
plt.show()
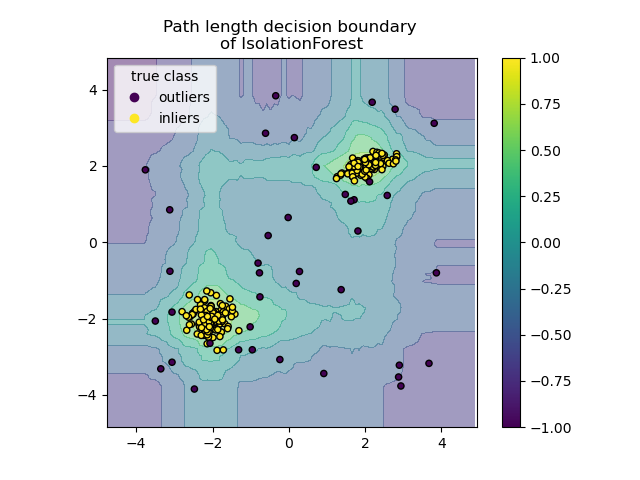
Plot path length decision boundary#
By setting the response_method="decision_function", the background of the
DecisionBoundaryDisplay represents the measure of
normality of an observation. Such score is given by the path length averaged
over a forest of random trees, which itself is given by the depth of the leaf
(or equivalently the number of splits) required to isolate a given sample.
When a forest of random trees collectively produce short path lengths for
isolating some particular samples, they are highly likely to be anomalies and
the measure of normality is close to 0. Similarly, large paths correspond to
values close to 1 and are more likely to be inliers.
disp = DecisionBoundaryDisplay.from_estimator(
clf,
X,
response_method="decision_function",
alpha=0.5,
)
disp.ax_.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor="k")
disp.ax_.set_title("Path length decision boundary \nof IsolationForest")
plt.axis("square")
plt.legend(handles=handles, labels=["outliers", "inliers"], title="true class")
plt.colorbar(disp.ax_.collections[1])
plt.show()
Total running time of the script: (0 minutes 0.436 seconds)
Related examples
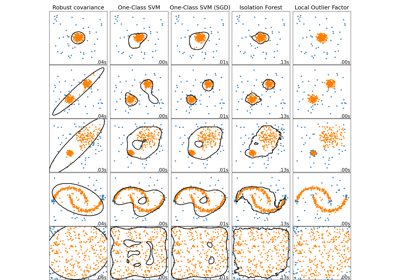
Comparing anomaly detection algorithms for outlier detection on toy datasets