Note

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

Isotonic Regression#

An illustration of the isotonic regression on generated data (non-linear monotonic trend with homoscedastic uniform noise).

The isotonic regression algorithm finds a non-decreasing approximation of a function while minimizing the mean squared error on the training data. The benefit of such a non-parametric model is that it does not assume any shape for the target function besides monotonicity. For comparison a linear regression is also presented.

The plot on the right-hand side shows the model prediction function that results from the linear interpolation of thresholds points. The thresholds points are a subset of the training input observations and their matching target values are computed by the isotonic non-parametric fit.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.collections import LineCollection

from sklearn.isotonic import IsotonicRegression
from sklearn.linear_model import LinearRegression
from sklearn.utils import check_random_state

n = 100
x = np.arange(n)
rs = check_random_state(0)
y = rs.randint(-50, 50, size=(n,)) + 50.0 * np.log1p(np.arange(n))

Fit IsotonicRegression and LinearRegression models:

ir = IsotonicRegression(out_of_bounds="clip")
y_ = ir.fit_transform(x, y)

lr = LinearRegression()
lr.fit(x[:, np.newaxis], y)  # x needs to be 2d for LinearRegression

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Plot results:

segments = [[[i, y[i]], [i, y_[i]]] for i in range(n)]
lc = LineCollection(segments, zorder=0)
lc.set_array(np.ones(len(y)))
lc.set_linewidths(np.full(n, 0.5))

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(12, 6))

ax0.plot(x, y, "C0.", markersize=12)
ax0.plot(x, y_, "C1.-", markersize=12)
ax0.plot(x, lr.predict(x[:, np.newaxis]), "C2-")
ax0.add_collection(lc)
ax0.legend(("Training data", "Isotonic fit", "Linear fit"), loc="lower right")
ax0.set_title("Isotonic regression fit on noisy data (n=%d)" % n)

x_test = np.linspace(-10, 110, 1000)
ax1.plot(x_test, ir.predict(x_test), "C1-")
ax1.plot(ir.X_thresholds_, ir.y_thresholds_, "C1.", markersize=12)
ax1.set_title("Prediction function (%d thresholds)" % len(ir.X_thresholds_))

plt.show()

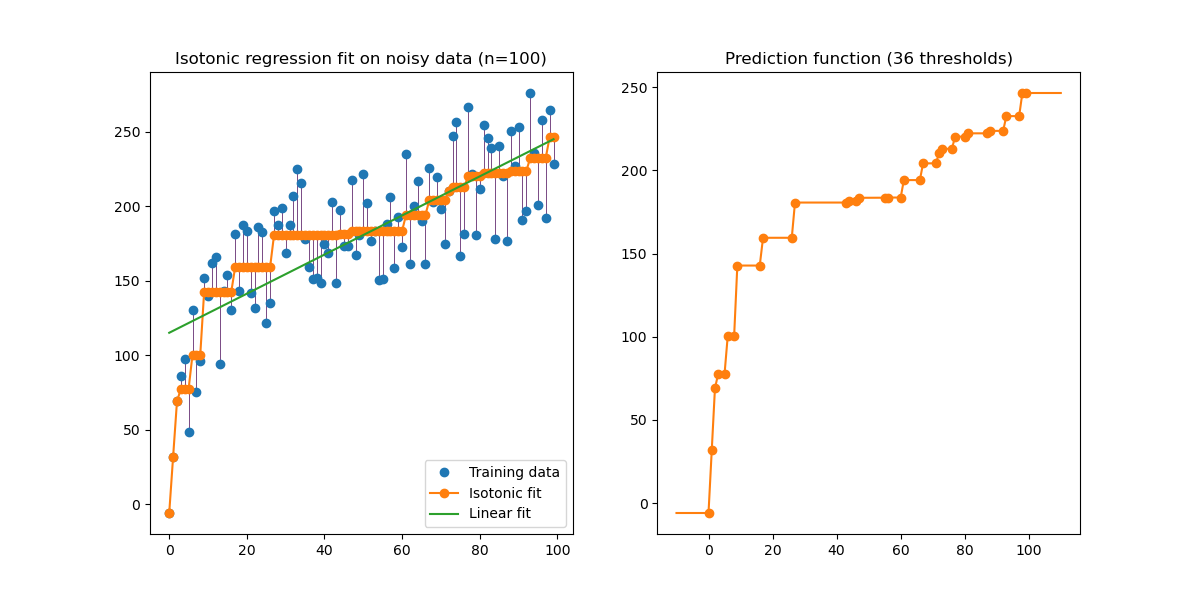
Isotonic regression fit on noisy data (n=100), Prediction function (36 thresholds)

Note that we explicitly passed out_of_bounds="clip" to the constructor of IsotonicRegression to control the way the model extrapolates outside of the range of data observed in the training set. This “clipping” extrapolation can be seen on the plot of the decision function on the right-hand.

Total running time of the script: (0 minutes 0.139 seconds)