BayesianGaussianMixture#
- class sklearn.mixture.BayesianGaussianMixture(*, n_components=1, covariance_type='full', tol=0.001, reg_covar=1e-06, max_iter=100, n_init=1, init_params='kmeans', weight_concentration_prior_type='dirichlet_process', weight_concentration_prior=None, mean_precision_prior=None, mean_prior=None, degrees_of_freedom_prior=None, covariance_prior=None, random_state=None, warm_start=False, verbose=0, verbose_interval=10)[source]#
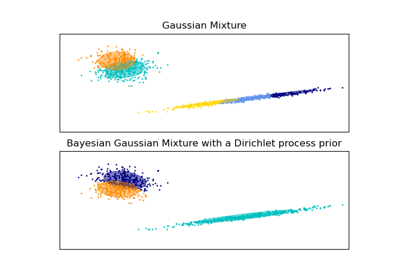
Variational Bayesian estimation of a Gaussian mixture.
This class allows to infer an approximate posterior distribution over the parameters of a Gaussian mixture distribution. The effective number of components can be inferred from the data.
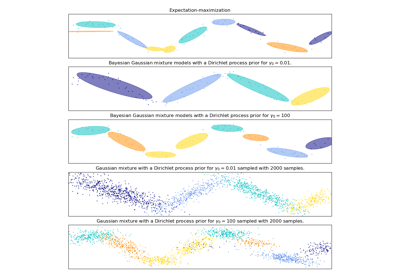
This class implements two types of prior for the weights distribution: a finite mixture model with Dirichlet distribution and an infinite mixture model with the Dirichlet Process. In practice Dirichlet Process inference algorithm is approximated and uses a truncated distribution with a fixed maximum number of components (called the Stick-breaking representation). The number of components actually used almost always depends on the data.
Added in version 0.18.
Read more in the User Guide.
- Parameters:
- n_componentsint, default=1
The number of mixture components. Depending on the data and the value of the
weight_concentration_priorthe model can decide to not use all the components by setting some componentweights_to values very close to zero. The number of effective components is therefore smaller than n_components.- covariance_type{‘full’, ‘tied’, ‘diag’, ‘spherical’}, default=’full’
String describing the type of covariance parameters to use. Must be one of:
‘full’ (each component has its own general covariance matrix),
‘tied’ (all components share the same general covariance matrix),
‘diag’ (each component has its own diagonal covariance matrix),
‘spherical’ (each component has its own single variance).
- tolfloat, default=1e-3
The convergence threshold. EM iterations will stop when the lower bound average gain on the likelihood (of the training data with respect to the model) is below this threshold.
- reg_covarfloat, default=1e-6
Non-negative regularization added to the diagonal of covariance. Allows to assure that the covariance matrices are all positive.
- max_iterint, default=100
The number of EM iterations to perform.
- n_initint, default=1
The number of initializations to perform. The result with the highest lower bound value on the likelihood is kept.
- init_params{‘kmeans’, ‘k-means++’, ‘random’, ‘random_from_data’}, default=’kmeans’
The method used to initialize the weights, the means and the covariances. String must be one of:
‘kmeans’: responsibilities are initialized using kmeans.
‘k-means++’: use the k-means++ method to initialize.
‘random’: responsibilities are initialized randomly.
‘random_from_data’: initial means are randomly selected data points.
Changed in version v1.1:
init_paramsnow accepts ‘random_from_data’ and ‘k-means++’ as initialization methods.- weight_concentration_prior_type{‘dirichlet_process’, ‘dirichlet_distribution’}, default=’dirichlet_process’
String describing the type of the weight concentration prior.
- weight_concentration_priorfloat or None, default=None
The dirichlet concentration of each component on the weight distribution (Dirichlet). This is commonly called gamma in the literature. The higher concentration puts more mass in the center and will lead to more components being active, while a lower concentration parameter will lead to more mass at the edge of the mixture weights simplex. The value of the parameter must be greater than 0. If it is None, it’s set to
1. / n_components.- mean_precision_priorfloat or None, default=None
The precision prior on the mean distribution (Gaussian). Controls the extent of where means can be placed. Larger values concentrate the cluster means around
mean_prior. The value of the parameter must be greater than 0. If it is None, it is set to 1.- mean_priorarray-like, shape (n_features,), default=None
The prior on the mean distribution (Gaussian). If it is None, it is set to the mean of X.
- degrees_of_freedom_priorfloat or None, default=None
The prior of the number of degrees of freedom on the covariance distributions (Wishart). If it is None, it’s set to
n_features.- covariance_priorfloat or array-like, default=None
The prior on the covariance distribution (Wishart). If it is None, the emiprical covariance prior is initialized using the covariance of X. The shape depends on
covariance_type:(n_features, n_features) if 'full', (n_features, n_features) if 'tied', (n_features) if 'diag', float if 'spherical'
- random_stateint, RandomState instance or None, default=None
Controls the random seed given to the method chosen to initialize the parameters (see
init_params). In addition, it controls the generation of random samples from the fitted distribution (see the methodsample). Pass an int for reproducible output across multiple function calls. See Glossary.- warm_startbool, default=False
If ‘warm_start’ is True, the solution of the last fitting is used as initialization for the next call of fit(). This can speed up convergence when fit is called several times on similar problems. See the Glossary.
- verboseint, default=0
Enable verbose output. If 1 then it prints the current initialization and each iteration step. If greater than 1 then it prints also the log probability and the time needed for each step.
- verbose_intervalint, default=10
Number of iteration done before the next print.
- Attributes:
- weights_array-like of shape (n_components,)
The weights of each mixture components.
- means_array-like of shape (n_components, n_features)
The mean of each mixture component.
- covariances_array-like
The covariance of each mixture component. The shape depends on
covariance_type:(n_components,) if 'spherical', (n_features, n_features) if 'tied', (n_components, n_features) if 'diag', (n_components, n_features, n_features) if 'full'
- precisions_array-like
The precision matrices for each component in the mixture. A precision matrix is the inverse of a covariance matrix. A covariance matrix is symmetric positive definite so the mixture of Gaussian can be equivalently parameterized by the precision matrices. Storing the precision matrices instead of the covariance matrices makes it more efficient to compute the log-likelihood of new samples at test time. The shape depends on
covariance_type:(n_components,) if 'spherical', (n_features, n_features) if 'tied', (n_components, n_features) if 'diag', (n_components, n_features, n_features) if 'full'
- precisions_cholesky_array-like
The Cholesky decomposition of the precision matrices of each mixture component. A precision matrix is the inverse of a covariance matrix. A covariance matrix is symmetric positive definite so the mixture of Gaussian can be equivalently parameterized by the precision matrices. Storing the precision matrices instead of the covariance matrices makes it more efficient to compute the log-likelihood of new samples at test time. The shape depends on
covariance_type:(n_components,) if 'spherical', (n_features, n_features) if 'tied', (n_components, n_features) if 'diag', (n_components, n_features, n_features) if 'full'
- converged_bool
True when convergence of the best fit of inference was reached, False otherwise.
- n_iter_int
Number of step used by the best fit of inference to reach the convergence.
- lower_bound_float
Lower bound value on the model evidence (of the training data) of the best fit of inference.
- lower_bounds_array-like of shape (
n_iter_,) The list of lower bound values on the model evidence from each iteration of the best fit of inference.
- weight_concentration_prior_tuple or float
The dirichlet concentration of each component on the weight distribution (Dirichlet). The type depends on
weight_concentration_prior_type:(float, float) if 'dirichlet_process' (Beta parameters), float if 'dirichlet_distribution' (Dirichlet parameters).
The higher concentration puts more mass in the center and will lead to more components being active, while a lower concentration parameter will lead to more mass at the edge of the simplex.
- weight_concentration_array-like of shape (n_components,)
The dirichlet concentration of each component on the weight distribution (Dirichlet).
- mean_precision_prior_float
The precision prior on the mean distribution (Gaussian). Controls the extent of where means can be placed. Larger values concentrate the cluster means around
mean_prior. If mean_precision_prior is set to None,mean_precision_prior_is set to 1.- mean_precision_array-like of shape (n_components,)
The precision of each components on the mean distribution (Gaussian).
- mean_prior_array-like of shape (n_features,)
The prior on the mean distribution (Gaussian).
- degrees_of_freedom_prior_float
The prior of the number of degrees of freedom on the covariance distributions (Wishart).
- degrees_of_freedom_array-like of shape (n_components,)
The number of degrees of freedom of each components in the model.
- covariance_prior_float or array-like
The prior on the covariance distribution (Wishart). The shape depends on
covariance_type:(n_features, n_features) if 'full', (n_features, n_features) if 'tied', (n_features) if 'diag', float if 'spherical'
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
GaussianMixtureFinite Gaussian mixture fit with EM.
References
Examples
>>> import numpy as np >>> from sklearn.mixture import BayesianGaussianMixture >>> X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [12, 4], [10, 7]]) >>> bgm = BayesianGaussianMixture(n_components=2, random_state=42).fit(X) >>> bgm.means_ array([[2.49 , 2.29], [8.45, 4.52 ]]) >>> bgm.predict([[0, 0], [9, 3]]) array([0, 1])
- fit(X, y=None)[source]#
Estimate model parameters with the EM algorithm.
The method fits the model
n_inittimes and sets the parameters with which the model has the largest likelihood or lower bound. Within each trial, the method iterates between E-step and M-step formax_itertimes until the change of likelihood or lower bound is less thantol, otherwise, aConvergenceWarningis raised. Ifwarm_startisTrue, thenn_initis ignored and a single initialization is performed upon the first call. Upon consecutive calls, training starts where it left off.- Parameters:
- Xarray-like of shape (n_samples, n_features)
List of n_features-dimensional data points. Each row corresponds to a single data point.
- yIgnored
Not used, present for API consistency by convention.
- Returns:
- selfobject
The fitted mixture.
- fit_predict(X, y=None)[source]#
Estimate model parameters using X and predict the labels for X.
The method fits the model
n_inittimes and sets the parameters with which the model has the largest likelihood or lower bound. Within each trial, the method iterates between E-step and M-step formax_itertimes until the change of likelihood or lower bound is less thantol, otherwise, aConvergenceWarningis raised. After fitting, it predicts the most probable label for the input data points.Added in version 0.20.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
List of n_features-dimensional data points. Each row corresponds to a single data point.
- yIgnored
Not used, present for API consistency by convention.
- Returns:
- labelsarray, shape (n_samples,)
Component labels.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- predict(X)[source]#
Predict the labels for the data samples in X using trained model.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
List of n_features-dimensional data points. Each row corresponds to a single data point.
- Returns:
- labelsarray, shape (n_samples,)
Component labels.
- predict_proba(X)[source]#
Evaluate the components’ density for each sample.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
List of n_features-dimensional data points. Each row corresponds to a single data point.
- Returns:
- resparray, shape (n_samples, n_components)
Density of each Gaussian component for each sample in X.
- sample(n_samples=1)[source]#
Generate random samples from the fitted Gaussian distribution.
- Parameters:
- n_samplesint, default=1
Number of samples to generate.
- Returns:
- Xarray, shape (n_samples, n_features)
Randomly generated sample.
- yarray, shape (nsamples,)
Component labels.
- score(X, y=None)[source]#
Compute the per-sample average log-likelihood of the given data X.
- Parameters:
- Xarray-like of shape (n_samples, n_dimensions)
List of n_features-dimensional data points. Each row corresponds to a single data point.
- yIgnored
Not used, present for API consistency by convention.
- Returns:
- log_likelihoodfloat
Log-likelihood of
Xunder the Gaussian mixture model.
- score_samples(X)[source]#
Compute the log-likelihood of each sample.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
List of n_features-dimensional data points. Each row corresponds to a single data point.
- Returns:
- log_probarray, shape (n_samples,)
Log-likelihood of each sample in
Xunder the current model.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
Gallery examples#
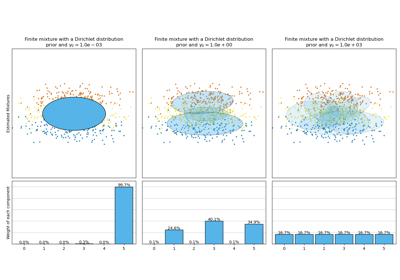
Concentration Prior Type Analysis of Variation Bayesian Gaussian Mixture