PowerTransformer#
- class sklearn.preprocessing.PowerTransformer(method='yeo-johnson', *, standardize=True, copy=True)[source]#
Apply a power transform featurewise to make data more Gaussian-like.
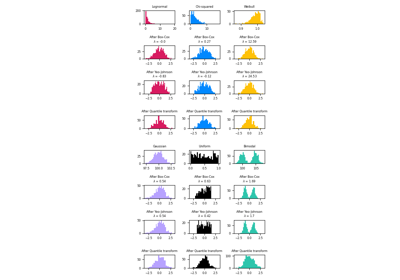
Power transforms are a family of parametric, monotonic transformations that are applied to make data more Gaussian-like. This is useful for modeling issues related to heteroscedasticity (non-constant variance), or other situations where normality is desired.
Currently, PowerTransformer supports the Box-Cox transform and the Yeo-Johnson transform. The optimal parameter for stabilizing variance and minimizing skewness is estimated through maximum likelihood.
Box-Cox requires input data to be strictly positive, while Yeo-Johnson supports both positive or negative data.
By default, zero-mean, unit-variance normalization is applied to the transformed data.
For an example visualization, refer to Compare PowerTransformer with other scalers. To see the effect of Box-Cox and Yeo-Johnson transformations on different distributions, see: Map data to a normal distribution.
Read more in the User Guide.
Added in version 0.20.
- Parameters:
- method{‘yeo-johnson’, ‘box-cox’}, default=’yeo-johnson’
The power transform method. Available methods are:
- standardizebool, default=True
Set to True to apply zero-mean, unit-variance normalization to the transformed output.
- copybool, default=True
Set to False to perform inplace computation during transformation.
- Attributes:
- lambdas_ndarray of float of shape (n_features,)
The parameters of the power transformation for the selected features.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
power_transformEquivalent function without the estimator API.
QuantileTransformerMaps data to a standard normal distribution with the parameter
output_distribution='normal'.
Notes
NaNs are treated as missing values: disregarded in
fit, and maintained intransform.References
[1]Examples
>>> import numpy as np >>> from sklearn.preprocessing import PowerTransformer >>> pt = PowerTransformer() >>> data = [[1, 2], [3, 2], [4, 5]] >>> print(pt.fit(data)) PowerTransformer() >>> print(pt.lambdas_) [ 1.386 -3.100] >>> print(pt.transform(data)) [[-1.316 -0.707] [ 0.209 -0.707] [ 1.106 1.414]]
- fit(X, y=None)[source]#
Estimate the optimal parameter lambda for each feature.
The optimal lambda parameter for minimizing skewness is estimated on each feature independently using maximum likelihood.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The data used to estimate the optimal transformation parameters.
- yNone
Ignored.
- Returns:
- selfobject
Fitted transformer.
- fit_transform(X, y=None)[source]#
Fit
PowerTransformertoX, then transformX.- Parameters:
- Xarray-like of shape (n_samples, n_features)
The data used to estimate the optimal transformation parameters and to be transformed using a power transformation.
- yIgnored
Not used, present for API consistency by convention.
- Returns:
- X_newndarray of shape (n_samples, n_features)
Transformed data.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
- Parameters:
- input_featuresarray-like of str or None, default=None
Input features.
If
input_featuresisNone, thenfeature_names_in_is used as feature names in. Iffeature_names_in_is not defined, then the following input feature names are generated:["x0", "x1", ..., "x(n_features_in_ - 1)"].If
input_featuresis an array-like, theninput_featuresmust matchfeature_names_in_iffeature_names_in_is defined.
- Returns:
- feature_names_outndarray of str objects
Same as input features.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- inverse_transform(X)[source]#
Apply the inverse power transformation using the fitted lambdas.
The inverse of the Box-Cox transformation is given by:
if lambda_ == 0: X_original = exp(X_trans) else: X_original = (X * lambda_ + 1) ** (1 / lambda_)
The inverse of the Yeo-Johnson transformation is given by:
if X >= 0 and lambda_ == 0: X_original = exp(X) - 1 elif X >= 0 and lambda_ != 0: X_original = (X * lambda_ + 1) ** (1 / lambda_) - 1 elif X < 0 and lambda_ != 2: X_original = 1 - (-(2 - lambda_) * X + 1) ** (1 / (2 - lambda_)) elif X < 0 and lambda_ == 2: X_original = 1 - exp(-X)
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The transformed data.
- Returns:
- X_originalndarray of shape (n_samples, n_features)
The original data.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
Gallery examples#
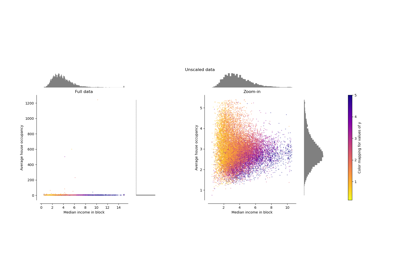
Compare the effect of different scalers on data with outliers