FactorAnalysis#
- class sklearn.decomposition.FactorAnalysis(n_components=None, *, tol=0.01, copy=True, max_iter=1000, noise_variance_init=None, svd_method='randomized', iterated_power=3, rotation=None, random_state=0)[source]#
Factor Analysis (FA).
A simple linear generative model with Gaussian latent variables.
The observations are assumed to be caused by a linear transformation of lower dimensional latent factors and added Gaussian noise. Without loss of generality the factors are distributed according to a Gaussian with zero mean and unit covariance. The noise is also zero mean and has an arbitrary diagonal covariance matrix.
If we would restrict the model further, by assuming that the Gaussian noise is even isotropic (all diagonal entries are the same) we would obtain
PCA.FactorAnalysis performs a maximum likelihood estimate of the so-called
loadingmatrix, the transformation of the latent variables to the observed ones, using SVD based approach.Read more in the User Guide.
Added in version 0.13.
- Parameters:
- n_componentsint, default=None
Dimensionality of latent space, the number of components of
Xthat are obtained aftertransform. If None, n_components is set to the number of features.- tolfloat, default=1e-2
Stopping tolerance for log-likelihood increase.
- copybool, default=True
Whether to make a copy of X. If
False, the input X gets overwritten during fitting.- max_iterint, default=1000
Maximum number of iterations.
- noise_variance_initarray-like of shape (n_features,), default=None
The initial guess of the noise variance for each feature. If None, it defaults to np.ones(n_features).
- svd_method{‘lapack’, ‘randomized’}, default=’randomized’
Which SVD method to use. If ‘lapack’ use standard SVD from scipy.linalg, if ‘randomized’ use fast
randomized_svdfunction. Defaults to ‘randomized’. For most applications ‘randomized’ will be sufficiently precise while providing significant speed gains. Accuracy can also be improved by setting higher values foriterated_power. If this is not sufficient, for maximum precision you should choose ‘lapack’.- iterated_powerint, default=3
Number of iterations for the power method. 3 by default. Only used if
svd_methodequals ‘randomized’.- rotation{‘varimax’, ‘quartimax’}, default=None
If not None, apply the indicated rotation. Currently, varimax and quartimax are implemented. See “The varimax criterion for analytic rotation in factor analysis” H. F. Kaiser, 1958.
Added in version 0.24.
- random_stateint or RandomState instance, default=0
Only used when
svd_methodequals ‘randomized’. Pass an int for reproducible results across multiple function calls. See Glossary.
- Attributes:
- components_ndarray of shape (n_components, n_features)
Components with maximum variance.
- loglike_list of shape (n_iterations,)
The log likelihood at each iteration.
- noise_variance_ndarray of shape (n_features,)
The estimated noise variance for each feature.
- n_iter_int
Number of iterations run.
- mean_ndarray of shape (n_features,)
Per-feature empirical mean, estimated from the training set.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
PCAPrincipal component analysis is also a latent linear variable model which however assumes equal noise variance for each feature. This extra assumption makes probabilistic PCA faster as it can be computed in closed form.
FastICAIndependent component analysis, a latent variable model with non-Gaussian latent variables.
References
David Barber, Bayesian Reasoning and Machine Learning, Algorithm 21.1.
Christopher M. Bishop: Pattern Recognition and Machine Learning, Chapter 12.2.4.
Examples
>>> from sklearn.datasets import load_digits >>> from sklearn.decomposition import FactorAnalysis >>> X, _ = load_digits(return_X_y=True) >>> transformer = FactorAnalysis(n_components=7, random_state=0) >>> X_transformed = transformer.fit_transform(X) >>> X_transformed.shape (1797, 7)
- fit(X, y=None)[source]#
Fit the FactorAnalysis model to X using SVD based approach.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Training data.
- yIgnored
Ignored parameter.
- Returns:
- selfobject
FactorAnalysis class instance.
- fit_transform(X, y=None, **fit_params)[source]#
Fit to data, then transform it.
Fits transformer to
Xandywith optional parametersfit_paramsand returns a transformed version ofX.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Input samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None
Target values (None for unsupervised transformations).
- **fit_paramsdict
Additional fit parameters. Pass only if the estimator accepts additional params in its
fitmethod.
- Returns:
- X_newndarray array of shape (n_samples, n_features_new)
Transformed array.
- get_covariance()[source]#
Compute data covariance with the FactorAnalysis model.
cov = components_.T * components_ + diag(noise_variance)- Returns:
- covndarray of shape (n_features, n_features)
Estimated covariance of data.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are:
["class_name0", "class_name1", "class_name2"].- Parameters:
- input_featuresarray-like of str or None, default=None
Only used to validate feature names with the names seen in
fit.
- Returns:
- feature_names_outndarray of str objects
Transformed feature names.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- get_precision()[source]#
Compute data precision matrix with the FactorAnalysis model.
- Returns:
- precisionndarray of shape (n_features, n_features)
Estimated precision of data.
- score(X, y=None)[source]#
Compute the average log-likelihood of the samples.
- Parameters:
- Xndarray of shape (n_samples, n_features)
The data.
- yIgnored
Ignored parameter.
- Returns:
- llfloat
Average log-likelihood of the samples under the current model.
- score_samples(X)[source]#
Compute the log-likelihood of each sample.
- Parameters:
- Xndarray of shape (n_samples, n_features)
The data.
- Returns:
- llndarray of shape (n_samples,)
Log-likelihood of each sample under the current model.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- transform(X)[source]#
Apply dimensionality reduction to X using the model.
Compute the expected mean of the latent variables. See Barber, 21.2.33 (or Bishop, 12.66).
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Training data.
- Returns:
- X_newndarray of shape (n_samples, n_components)
The latent variables of X.
Gallery examples#
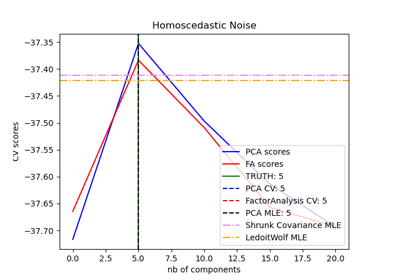
Model selection with Probabilistic PCA and Factor Analysis (FA)
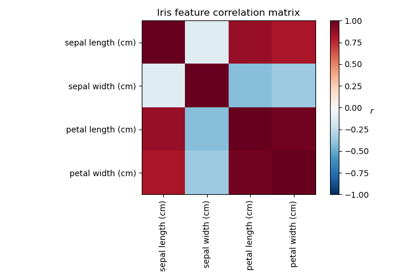
Factor Analysis (with rotation) to visualize patterns
