KNeighborsClassifier#
- class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)[source]#
Classifier implementing the k-nearest neighbors vote.
Read more in the User Guide.
- Parameters:
- n_neighborsint, default=5
Number of neighbors to use by default for
kneighborsqueries.- weights{‘uniform’, ‘distance’}, callable or None, default=’uniform’
Weight function used in prediction. Possible values:
‘uniform’ : uniform weights. All points in each neighborhood are weighted equally.
‘distance’ : weight points by the inverse of their distance. in this case, closer neighbors of a query point will have a greater influence than neighbors which are further away.
[callable] : a user-defined function which accepts an array of distances, and returns an array of the same shape containing the weights.
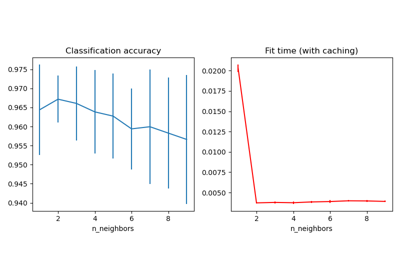
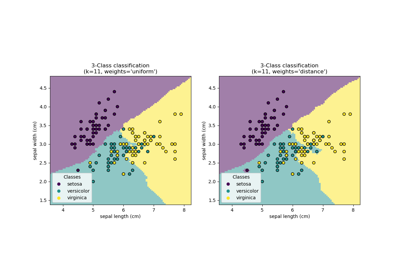
Refer to the example entitled Nearest Neighbors Classification showing the impact of the
weightsparameter on the decision boundary.- algorithm{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’
Algorithm used to compute the nearest neighbors:
‘ball_tree’ will use
BallTree‘kd_tree’ will use
KDTree‘brute’ will use a brute-force search.
‘auto’ will attempt to decide the most appropriate algorithm based on the values passed to
fitmethod.
Note: fitting on sparse input will override the setting of this parameter, using brute force.
- leaf_sizeint, default=30
Leaf size passed to BallTree or KDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.
- pfloat, default=2
Power parameter for the Minkowski metric. When p = 1, this is equivalent to using manhattan_distance (l1), and euclidean_distance (l2) for p = 2. For arbitrary p, minkowski_distance (l_p) is used. This parameter is expected to be positive.
- metricstr or callable, default=’minkowski’
Metric to use for distance computation. Default is “minkowski”, which results in the standard Euclidean distance when p = 2. See the documentation of scipy.spatial.distance and the metrics listed in
distance_metricsfor valid metric values.If metric is “precomputed”, X is assumed to be a distance matrix and must be square during fit. X may be a sparse graph, in which case only “nonzero” elements may be considered neighbors.
If metric is a callable function, it takes two arrays representing 1D vectors as inputs and must return one value indicating the distance between those vectors. This works for Scipy’s metrics, but is less efficient than passing the metric name as a string.
- metric_paramsdict, default=None
Additional keyword arguments for the metric function.
- n_jobsint, default=None
The number of parallel jobs to run for neighbors search.
Nonemeans 1 unless in ajoblib.parallel_backendcontext.-1means using all processors. See Glossary for more details. Doesn’t affectfitmethod.
- Attributes:
- classes_array of shape (n_classes,)
Class labels known to the classifier
- effective_metric_str or callble
The distance metric used. It will be same as the
metricparameter or a synonym of it, e.g. ‘euclidean’ if themetricparameter set to ‘minkowski’ andpparameter set to 2.- effective_metric_params_dict
Additional keyword arguments for the metric function. For most metrics will be same with
metric_paramsparameter, but may also contain thepparameter value if theeffective_metric_attribute is set to ‘minkowski’.- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
- n_samples_fit_int
Number of samples in the fitted data.
- outputs_2d_bool
False when
y’s shape is (n_samples, ) or (n_samples, 1) during fit otherwise True.
See also
RadiusNeighborsClassifierClassifier based on neighbors within a fixed radius.
KNeighborsRegressorRegression based on k-nearest neighbors.
RadiusNeighborsRegressorRegression based on neighbors within a fixed radius.
NearestNeighborsUnsupervised learner for implementing neighbor searches.
Notes
See Nearest Neighbors in the online documentation for a discussion of the choice of
algorithmandleaf_size.Warning
Regarding the Nearest Neighbors algorithms, if it is found that two neighbors, neighbor
k+1andk, have identical distances but different labels, the results will depend on the ordering of the training data.https://en.wikipedia.org/wiki/K-nearest_neighbor_algorithm
Examples
>>> X = [[0], [1], [2], [3]] >>> y = [0, 0, 1, 1] >>> from sklearn.neighbors import KNeighborsClassifier >>> neigh = KNeighborsClassifier(n_neighbors=3) >>> neigh.fit(X, y) KNeighborsClassifier(...) >>> print(neigh.predict([[1.1]])) [0] >>> print(neigh.predict_proba([[0.9]])) [[0.666 0.333]]
- fit(X, y)[source]#
Fit the k-nearest neighbors classifier from the training dataset.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features) or (n_samples, n_samples) if metric=’precomputed’
Training data.
- y{array-like, sparse matrix} of shape (n_samples,) or (n_samples, n_outputs)
Target values.
- Returns:
- selfKNeighborsClassifier
The fitted k-nearest neighbors classifier.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- kneighbors(X=None, n_neighbors=None, return_distance=True)[source]#
Find the K-neighbors of a point.
Returns indices of and distances to the neighbors of each point.
- Parameters:
- X{array-like, sparse matrix}, shape (n_queries, n_features), or (n_queries, n_indexed) if metric == ‘precomputed’, default=None
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
- n_neighborsint, default=None
Number of neighbors required for each sample. The default is the value passed to the constructor.
- return_distancebool, default=True
Whether or not to return the distances.
- Returns:
- neigh_distndarray of shape (n_queries, n_neighbors)
Array representing the lengths to points, only present if return_distance=True.
- neigh_indndarray of shape (n_queries, n_neighbors)
Indices of the nearest points in the population matrix.
Examples
In the following example, we construct a NearestNeighbors class from an array representing our data set and ask who’s the closest point to [1,1,1]
>>> samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]] >>> from sklearn.neighbors import NearestNeighbors >>> neigh = NearestNeighbors(n_neighbors=1) >>> neigh.fit(samples) NearestNeighbors(n_neighbors=1) >>> print(neigh.kneighbors([[1., 1., 1.]])) (array([[0.5]]), array([[2]]))
As you can see, it returns [[0.5]], and [[2]], which means that the element is at distance 0.5 and is the third element of samples (indexes start at 0). You can also query for multiple points:
>>> X = [[0., 1., 0.], [1., 0., 1.]] >>> neigh.kneighbors(X, return_distance=False) array([[1], [2]]...)
- kneighbors_graph(X=None, n_neighbors=None, mode='connectivity')[source]#
Compute the (weighted) graph of k-Neighbors for points in X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_queries, n_features), or (n_queries, n_indexed) if metric == ‘precomputed’, default=None
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor. For
metric='precomputed'the shape should be (n_queries, n_indexed). Otherwise the shape should be (n_queries, n_features).- n_neighborsint, default=None
Number of neighbors for each sample. The default is the value passed to the constructor.
- mode{‘connectivity’, ‘distance’}, default=’connectivity’
Type of returned matrix: ‘connectivity’ will return the connectivity matrix with ones and zeros, in ‘distance’ the edges are distances between points, type of distance depends on the selected metric parameter in NearestNeighbors class.
- Returns:
- Asparse-matrix of shape (n_queries, n_samples_fit)
n_samples_fitis the number of samples in the fitted data.A[i, j]gives the weight of the edge connectingitoj. The matrix is of CSR format.
See also
NearestNeighbors.radius_neighbors_graphCompute the (weighted) graph of Neighbors for points in X.
Examples
>>> X = [[0], [3], [1]] >>> from sklearn.neighbors import NearestNeighbors >>> neigh = NearestNeighbors(n_neighbors=2) >>> neigh.fit(X) NearestNeighbors(n_neighbors=2) >>> A = neigh.kneighbors_graph(X) >>> A.toarray() array([[1., 0., 1.], [0., 1., 1.], [1., 0., 1.]])
- predict(X)[source]#
Predict the class labels for the provided data.
- Parameters:
- X{array-like, sparse matrix} of shape (n_queries, n_features), or (n_queries, n_indexed) if metric == ‘precomputed’, or None
Test samples. If
None, predictions for all indexed points are returned; in this case, points are not considered their own neighbors.
- Returns:
- yndarray of shape (n_queries,) or (n_queries, n_outputs)
Class labels for each data sample.
- predict_proba(X)[source]#
Return probability estimates for the test data X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_queries, n_features), or (n_queries, n_indexed) if metric == ‘precomputed’, or None
Test samples. If
None, predictions for all indexed points are returned; in this case, points are not considered their own neighbors.
- Returns:
- pndarray of shape (n_queries, n_classes), or a list of n_outputs of such arrays if n_outputs > 1.
The class probabilities of the input samples. Classes are ordered by lexicographic order.
- score(X, y, sample_weight=None)[source]#
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
- Parameters:
- Xarray-like of shape (n_samples, n_features), or None
Test samples. If
None, predictions for all indexed points are used; in this case, points are not considered their own neighbors. This means thatknn.fit(X, y).score(None, y)implicitly performs a leave-one-out cross-validation procedure and is equivalent tocross_val_score(knn, X, y, cv=LeaveOneOut())but typically much faster.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True labels for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
Mean accuracy of
self.predict(X)w.r.t.y.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') KNeighborsClassifier[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
Gallery examples#
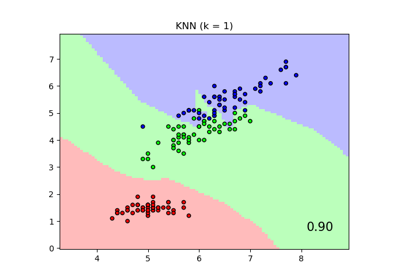
Comparing Nearest Neighbors with and without Neighborhood Components Analysis
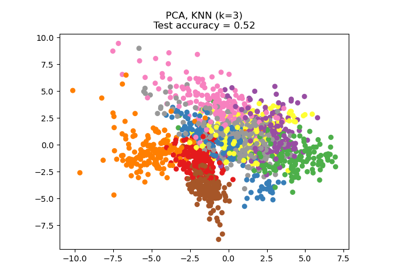
Dimensionality Reduction with Neighborhood Components Analysis
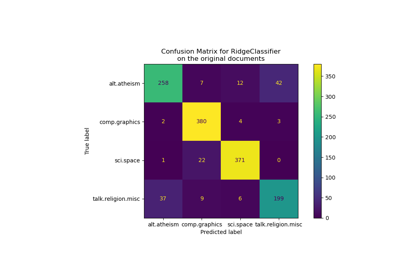
Classification of text documents using sparse features