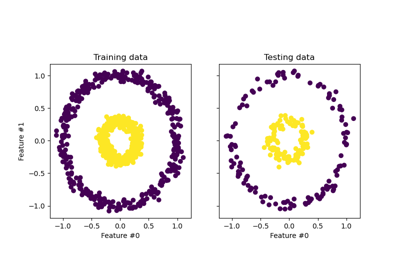
KernelRidge#
- class sklearn.kernel_ridge.KernelRidge(alpha=1, *, kernel='linear', gamma=None, degree=3, coef0=1, kernel_params=None)[source]#
Kernel ridge regression.
Kernel ridge regression (KRR) combines ridge regression (linear least squares with l2-norm regularization) with the kernel trick. It thus learns a linear function in the space induced by the respective kernel and the data. For non-linear kernels, this corresponds to a non-linear function in the original space.
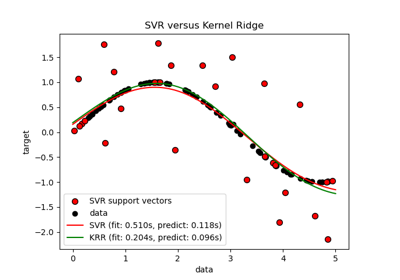
The form of the model learned by KRR is identical to support vector regression (SVR). However, different loss functions are used: KRR uses squared error loss while support vector regression uses epsilon-insensitive loss, both combined with l2 regularization. In contrast to SVR, fitting a KRR model can be done in closed-form and is typically faster for medium-sized datasets. On the other hand, the learned model is non-sparse and thus slower than SVR, which learns a sparse model for epsilon > 0, at prediction-time.
This estimator has built-in support for multi-variate regression (i.e., when y is a 2d-array of shape [n_samples, n_targets]).
Read more in the User Guide.
- Parameters:
- alphafloat or array-like of shape (n_targets,), default=1.0
Regularization strength; must be a positive float. Regularization improves the conditioning of the problem and reduces the variance of the estimates. Larger values specify stronger regularization. Alpha corresponds to
1 / (2C)in other linear models such asLogisticRegressionorLinearSVC. If an array is passed, penalties are assumed to be specific to the targets. Hence they must correspond in number. See Ridge regression and classification for formula.- kernelstr or callable, default=”linear”
Kernel mapping used internally. This parameter is directly passed to
pairwise_kernels. Ifkernelis a string, it must be one of the metrics inpairwise.PAIRWISE_KERNEL_FUNCTIONSor “precomputed”. Ifkernelis “precomputed”, X is assumed to be a kernel matrix. Alternatively, ifkernelis a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two rows from X as input and return the corresponding kernel value as a single number. This means that callables fromsklearn.metrics.pairwiseare not allowed, as they operate on matrices, not single samples. Use the string identifying the kernel instead.- gammafloat, default=None
Gamma parameter for the RBF, laplacian, polynomial, exponential chi2 and sigmoid kernels. Interpretation of the default value is left to the kernel; see the documentation for sklearn.metrics.pairwise. Ignored by other kernels.
- degreefloat, default=3
Degree of the polynomial kernel. Ignored by other kernels.
- coef0float, default=1
Zero coefficient for polynomial and sigmoid kernels. Ignored by other kernels.
- kernel_paramsdict, default=None
Additional parameters (keyword arguments) for kernel function passed as callable object.
- Attributes:
- dual_coef_ndarray of shape (n_samples,) or (n_samples, n_targets)
Representation of weight vector(s) in kernel space
- X_fit_{ndarray, sparse matrix} of shape (n_samples, n_features)
Training data, which is also required for prediction. If kernel == “precomputed” this is instead the precomputed training matrix, of shape (n_samples, n_samples).
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
sklearn.gaussian_process.GaussianProcessRegressorGaussian Process regressor providing automatic kernel hyperparameters tuning and predictions uncertainty.
sklearn.linear_model.RidgeLinear ridge regression.
sklearn.linear_model.RidgeCVRidge regression with built-in cross-validation.
sklearn.svm.SVRSupport Vector Regression accepting a large variety of kernels.
References
Kevin P. Murphy “Machine Learning: A Probabilistic Perspective”, The MIT Press chapter 14.4.3, pp. 492-493
Examples
>>> from sklearn.kernel_ridge import KernelRidge >>> import numpy as np >>> n_samples, n_features = 10, 5 >>> rng = np.random.RandomState(0) >>> y = rng.randn(n_samples) >>> X = rng.randn(n_samples, n_features) >>> krr = KernelRidge(alpha=1.0) >>> krr.fit(X, y) KernelRidge(alpha=1.0)
- fit(X, y, sample_weight=None)[source]#
Fit Kernel Ridge regression model.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training data. If kernel == “precomputed” this is instead a precomputed kernel matrix, of shape (n_samples, n_samples).
- yarray-like of shape (n_samples,) or (n_samples, n_targets)
Target values.
- sample_weightfloat or array-like of shape (n_samples,), default=None
Individual weights for each sample, ignored if None is passed.
- Returns:
- selfobject
Returns the instance itself.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- predict(X)[source]#
Predict using the kernel ridge model.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Samples. If kernel == “precomputed” this is instead a precomputed kernel matrix, shape = [n_samples, n_samples_fitted], where n_samples_fitted is the number of samples used in the fitting for this estimator.
- Returns:
- Cndarray of shape (n_samples,) or (n_samples, n_targets)
Returns predicted values.
- score(X, y, sample_weight=None)[source]#
Return coefficient of determination on test data.
The coefficient of determination, \(R^2\), is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares
((y_true - y_pred)** 2).sum()and \(v\) is the total sum of squares((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value ofy, disregarding the input features, would get a \(R^2\) score of 0.0.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape
(n_samples, n_samples_fitted), wheren_samples_fittedis the number of samples used in the fitting for the estimator.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True values for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
\(R^2\) of
self.predict(X)w.r.t.y.
Notes
The \(R^2\) score used when calling
scoreon a regressor usesmultioutput='uniform_average'from version 0.23 to keep consistent with default value ofr2_score. This influences thescoremethod of all the multioutput regressors (except forMultiOutputRegressor).
- set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') KernelRidge[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') KernelRidge[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
Gallery examples#
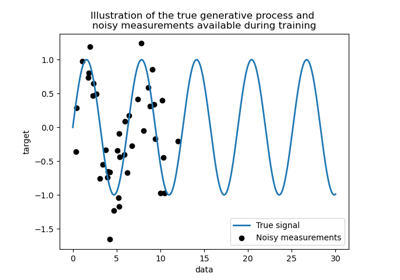
Comparison of kernel ridge and Gaussian process regression