mutual_info_regression#
- sklearn.feature_selection.mutual_info_regression(X, y, *, discrete_features='auto', n_neighbors=3, copy=True, random_state=None, n_jobs=None)[source]#
Estimate mutual information for a continuous target variable.
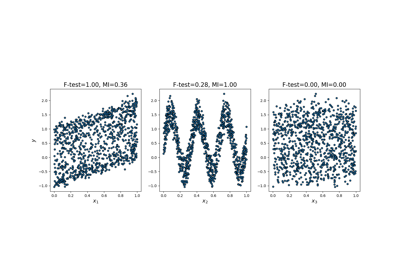
Mutual information (MI) [1] between two random variables is a non-negative value, which measures the dependency between the variables. It is equal to zero if and only if two random variables are independent, and higher values mean higher dependency.
The function relies on nonparametric methods based on entropy estimation from k-nearest neighbors distances as described in [2] and [3]. Both methods are based on the idea originally proposed in [4].
It can be used for univariate features selection, read more in the User Guide.
- Parameters:
- Xarray-like or sparse matrix, shape (n_samples, n_features)
Feature matrix.
- yarray-like of shape (n_samples,)
Target vector.
- discrete_features{‘auto’, bool, array-like}, default=’auto’
If bool, then determines whether to consider all features discrete or continuous. If array, then it should be either a boolean mask with shape (n_features,) or array with indices of discrete features. If ‘auto’, it is assigned to False for dense
Xand to True for sparseX.- n_neighborsint, default=3
Number of neighbors to use for MI estimation for continuous variables, see [2] and [3]. Higher values reduce variance of the estimation, but could introduce a bias.
- copybool, default=True
Whether to make a copy of the given data. If set to False, the initial data will be overwritten.
- random_stateint, RandomState instance or None, default=None
Determines random number generation for adding small noise to continuous variables in order to remove repeated values. Pass an int for reproducible results across multiple function calls. See Glossary.
- n_jobsint, default=None
The number of jobs to use for computing the mutual information. The parallelization is done on the columns of
X.Nonemeans 1 unless in ajoblib.parallel_backendcontext.-1means using all processors. See Glossary for more details.Added in version 1.5.
- Returns:
- mindarray, shape (n_features,)
Estimated mutual information between each feature and the target in nat units.
Notes
The term “discrete features” is used instead of naming them “categorical”, because it describes the essence more accurately. For example, pixel intensities of an image are discrete features (but hardly categorical) and you will get better results if mark them as such. Also note, that treating a continuous variable as discrete and vice versa will usually give incorrect results, so be attentive about that.
True mutual information can’t be negative. If its estimate turns out to be negative, it is replaced by zero.
References
[1]Mutual Information on Wikipedia.
[2] (1,2)A. Kraskov, H. Stogbauer and P. Grassberger, “Estimating mutual information”. Phys. Rev. E 69, 2004.
[3] (1,2)B. C. Ross “Mutual Information between Discrete and Continuous Data Sets”. PLoS ONE 9(2), 2014.
[4]L. F. Kozachenko, N. N. Leonenko, “Sample Estimate of the Entropy of a Random Vector”, Probl. Peredachi Inf., 23:2 (1987), 9-16
Examples
>>> from sklearn.datasets import make_regression >>> from sklearn.feature_selection import mutual_info_regression >>> X, y = make_regression( ... n_samples=50, n_features=3, n_informative=1, noise=1e-4, random_state=42 ... ) >>> mutual_info_regression(X, y) array([0.117, 2.645, 0.0287])