MLPRegressor#
- class sklearn.neural_network.MLPRegressor(loss='squared_error', hidden_layer_sizes=(100,), activation='relu', *, solver='adam', alpha=0.0001, batch_size='auto', learning_rate='constant', learning_rate_init=0.001, power_t=0.5, max_iter=200, shuffle=True, random_state=None, tol=0.0001, verbose=False, warm_start=False, momentum=0.9, nesterovs_momentum=True, early_stopping=False, validation_fraction=0.1, beta_1=0.9, beta_2=0.999, epsilon=1e-08, n_iter_no_change=10, max_fun=15000)[source]#
Multi-layer Perceptron regressor.
This model optimizes the squared error using LBFGS or stochastic gradient descent.
Added in version 0.18.
- Parameters:
- loss{‘squared_error’, ‘poisson’}, default=’squared_error’
The loss function to use when training the weights. Note that the “squared error” and “poisson” losses actually implement “half squares error” and “half poisson deviance” to simplify the computation of the gradient. Furthermore, the “poisson” loss internally uses a log-link (exponential as the output activation function) and requires
y >= 0.Changed in version 1.7: Added parameter
lossand option ‘poisson’.- hidden_layer_sizesarray-like of shape(n_layers - 2,), default=(100,)
The ith element represents the number of neurons in the ith hidden layer.
- activation{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, default=’relu’
Activation function for the hidden layer.
‘identity’, no-op activation, useful to implement linear bottleneck, returns f(x) = x
‘logistic’, the logistic sigmoid function, returns f(x) = 1 / (1 + exp(-x)).
‘tanh’, the hyperbolic tan function, returns f(x) = tanh(x).
‘relu’, the rectified linear unit function, returns f(x) = max(0, x)
- solver{‘lbfgs’, ‘sgd’, ‘adam’}, default=’adam’
The solver for weight optimization.
‘lbfgs’ is an optimizer in the family of quasi-Newton methods.
‘sgd’ refers to stochastic gradient descent.
‘adam’ refers to a stochastic gradient-based optimizer proposed by Kingma, Diederik, and Jimmy Ba
For a comparison between Adam optimizer and SGD, see Compare Stochastic learning strategies for MLPClassifier.
Note: The default solver ‘adam’ works pretty well on relatively large datasets (with thousands of training samples or more) in terms of both training time and validation score. For small datasets, however, ‘lbfgs’ can converge faster and perform better.
- alphafloat, default=0.0001
Strength of the L2 regularization term. The L2 regularization term is divided by the sample size when added to the loss.
- batch_sizeint, default=’auto’
Size of minibatches for stochastic optimizers. If the solver is ‘lbfgs’, the regressor will not use minibatch. When set to “auto”,
batch_size=min(200, n_samples).- learning_rate{‘constant’, ‘invscaling’, ‘adaptive’}, default=’constant’
Learning rate schedule for weight updates.
‘constant’ is a constant learning rate given by ‘learning_rate_init’.
‘invscaling’ gradually decreases the learning rate
learning_rate_at each time step ‘t’ using an inverse scaling exponent of ‘power_t’. effective_learning_rate = learning_rate_init / pow(t, power_t)‘adaptive’ keeps the learning rate constant to ‘learning_rate_init’ as long as training loss keeps decreasing. Each time two consecutive epochs fail to decrease training loss by at least tol, or fail to increase validation score by at least tol if ‘early_stopping’ is on, the current learning rate is divided by 5.
Only used when solver=’sgd’.
- learning_rate_initfloat, default=0.001
The initial learning rate used. It controls the step-size in updating the weights. Only used when solver=’sgd’ or ‘adam’.
- power_tfloat, default=0.5
The exponent for inverse scaling learning rate. It is used in updating effective learning rate when the learning_rate is set to ‘invscaling’. Only used when solver=’sgd’.
- max_iterint, default=200
Maximum number of iterations. The solver iterates until convergence (determined by ‘tol’) or this number of iterations. For stochastic solvers (‘sgd’, ‘adam’), note that this determines the number of epochs (how many times each data point will be used), not the number of gradient steps.
- shufflebool, default=True
Whether to shuffle samples in each iteration. Only used when solver=’sgd’ or ‘adam’.
- random_stateint, RandomState instance, default=None
Determines random number generation for weights and bias initialization, train-test split if early stopping is used, and batch sampling when solver=’sgd’ or ‘adam’. Pass an int for reproducible results across multiple function calls. See Glossary.
- tolfloat, default=1e-4
Tolerance for the optimization. When the loss or score is not improving by at least
tolforn_iter_no_changeconsecutive iterations, unlesslearning_rateis set to ‘adaptive’, convergence is considered to be reached and training stops.- verbosebool, default=False
Whether to print progress messages to stdout.
- warm_startbool, default=False
When set to True, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. See the Glossary.
- momentumfloat, default=0.9
Momentum for gradient descent update. Should be between 0 and 1. Only used when solver=’sgd’.
- nesterovs_momentumbool, default=True
Whether to use Nesterov’s momentum. Only used when solver=’sgd’ and momentum > 0.
- early_stoppingbool, default=False
Whether to use early stopping to terminate training when validation score is not improving. If set to True, it will automatically set aside
validation_fractionof training data as validation and terminate training when validation score is not improving by at leasttolforn_iter_no_changeconsecutive epochs. Only effective when solver=’sgd’ or ‘adam’.- validation_fractionfloat, default=0.1
The proportion of training data to set aside as validation set for early stopping. Must be between 0 and 1. Only used if early_stopping is True.
- beta_1float, default=0.9
Exponential decay rate for estimates of first moment vector in adam, should be in [0, 1). Only used when solver=’adam’.
- beta_2float, default=0.999
Exponential decay rate for estimates of second moment vector in adam, should be in [0, 1). Only used when solver=’adam’.
- epsilonfloat, default=1e-8
Value for numerical stability in adam. Only used when solver=’adam’.
- n_iter_no_changeint, default=10
Maximum number of epochs to not meet
tolimprovement. Only effective when solver=’sgd’ or ‘adam’.Added in version 0.20.
- max_funint, default=15000
Only used when solver=’lbfgs’. Maximum number of function calls. The solver iterates until convergence (determined by
tol), number of iterations reaches max_iter, or this number of function calls. Note that number of function calls will be greater than or equal to the number of iterations for the MLPRegressor.Added in version 0.22.
- Attributes:
- loss_float
The current loss computed with the loss function.
- best_loss_float
The minimum loss reached by the solver throughout fitting. If
early_stopping=True, this attribute is set toNone. Refer to thebest_validation_score_fitted attribute instead. Only accessible when solver=’sgd’ or ‘adam’.- loss_curve_list of shape (
n_iter_,) Loss value evaluated at the end of each training step. The ith element in the list represents the loss at the ith iteration. Only accessible when solver=’sgd’ or ‘adam’.
- validation_scores_list of shape (
n_iter_,) or None The score at each iteration on a held-out validation set. The score reported is the R2 score. Only available if
early_stopping=True, otherwise the attribute is set toNone. Only accessible when solver=’sgd’ or ‘adam’.- best_validation_score_float or None
The best validation score (i.e. R2 score) that triggered the early stopping. Only available if
early_stopping=True, otherwise the attribute is set toNone. Only accessible when solver=’sgd’ or ‘adam’.- t_int
The number of training samples seen by the solver during fitting. Mathematically equals
n_iters * X.shape[0], it meanstime_stepand it is used by optimizer’s learning rate scheduler.- coefs_list of shape (n_layers - 1,)
The ith element in the list represents the weight matrix corresponding to layer i.
- intercepts_list of shape (n_layers - 1,)
The ith element in the list represents the bias vector corresponding to layer i + 1.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
- n_iter_int
The number of iterations the solver has run.
- n_layers_int
Number of layers.
- n_outputs_int
Number of outputs.
- out_activation_str
Name of the output activation function.
See also
BernoulliRBMBernoulli Restricted Boltzmann Machine (RBM).
MLPClassifierMulti-layer Perceptron classifier.
sklearn.linear_model.SGDRegressorLinear model fitted by minimizing a regularized empirical loss with SGD.
Notes
MLPRegressor trains iteratively since at each time step the partial derivatives of the loss function with respect to the model parameters are computed to update the parameters.
It can also have a regularization term added to the loss function that shrinks model parameters to prevent overfitting.
This implementation works with data represented as dense and sparse numpy arrays of floating point values.
References
Hinton, Geoffrey E. “Connectionist learning procedures.” Artificial intelligence 40.1 (1989): 185-234.
Glorot, Xavier, and Yoshua Bengio. “Understanding the difficulty of training deep feedforward neural networks.” International Conference on Artificial Intelligence and Statistics. 2010.
Kingma, Diederik, and Jimmy Ba (2014) “Adam: A method for stochastic optimization.”
Examples
>>> from sklearn.neural_network import MLPRegressor >>> from sklearn.datasets import make_regression >>> from sklearn.model_selection import train_test_split >>> X, y = make_regression(n_samples=200, n_features=20, random_state=1) >>> X_train, X_test, y_train, y_test = train_test_split(X, y, ... random_state=1) >>> regr = MLPRegressor(random_state=1, max_iter=2000, tol=0.1) >>> regr.fit(X_train, y_train) MLPRegressor(max_iter=2000, random_state=1, tol=0.1) >>> regr.predict(X_test[:2]) array([ 28.98, -291]) >>> regr.score(X_test, y_test) 0.98
- fit(X, y, sample_weight=None)[source]#
Fit the model to data matrix X and target(s) y.
- Parameters:
- Xndarray or sparse matrix of shape (n_samples, n_features)
The input data.
- yndarray of shape (n_samples,) or (n_samples, n_outputs)
The target values (class labels in classification, real numbers in regression).
- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
Added in version 1.7.
- Returns:
- selfobject
Returns a trained MLP model.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- partial_fit(X, y, sample_weight=None)[source]#
Update the model with a single iteration over the given data.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input data.
- yndarray of shape (n_samples,)
The target values.
- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
Added in version 1.6.
- Returns:
- selfobject
Trained MLP model.
- predict(X)[source]#
Predict using the multi-layer perceptron model.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input data.
- Returns:
- yndarray of shape (n_samples, n_outputs)
The predicted values.
- score(X, y, sample_weight=None)[source]#
Return coefficient of determination on test data.
The coefficient of determination, \(R^2\), is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares
((y_true - y_pred)** 2).sum()and \(v\) is the total sum of squares((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value ofy, disregarding the input features, would get a \(R^2\) score of 0.0.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape
(n_samples, n_samples_fitted), wheren_samples_fittedis the number of samples used in the fitting for the estimator.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True values for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
\(R^2\) of
self.predict(X)w.r.t.y.
Notes
The \(R^2\) score used when calling
scoreon a regressor usesmultioutput='uniform_average'from version 0.23 to keep consistent with default value ofr2_score. This influences thescoremethod of all the multioutput regressors (except forMultiOutputRegressor).
- set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') MLPRegressor[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_partial_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') MLPRegressor[source]#
Configure whether metadata should be requested to be passed to the
partial_fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed topartial_fitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it topartial_fit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inpartial_fit.
- Returns:
- selfobject
The updated object.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') MLPRegressor[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
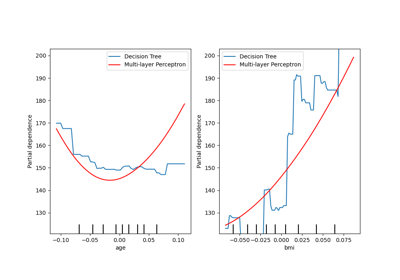
Gallery examples#
Partial Dependence and Individual Conditional Expectation Plots