Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder.
Comparing anomaly detection algorithms for outlier detection on toy datasets#
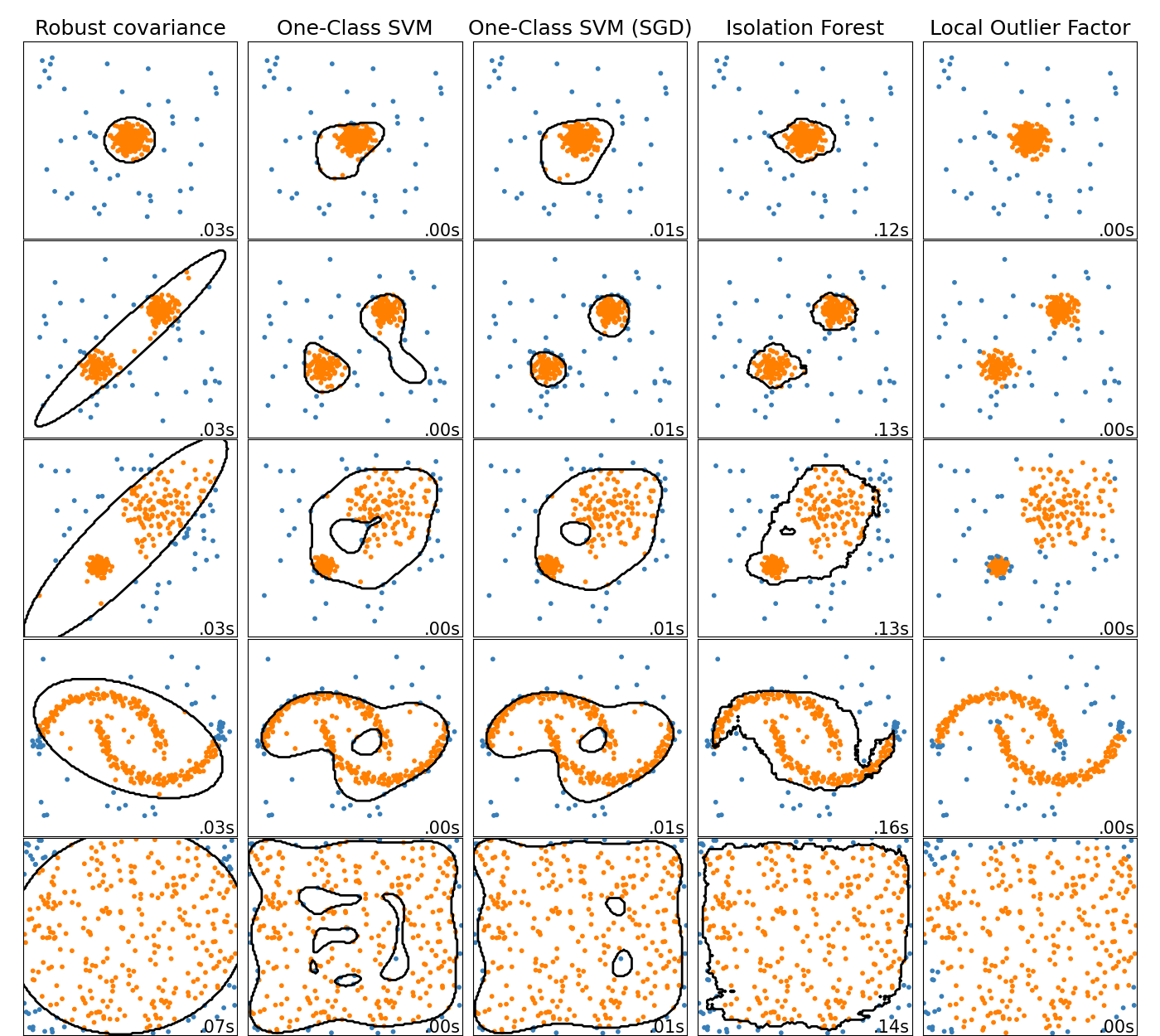
This example shows characteristics of different anomaly detection algorithms on 2D datasets. Datasets contain one or two modes (regions of high density) to illustrate the ability of algorithms to cope with multimodal data.
For each dataset, 15% of samples are generated as random uniform noise. This proportion is the value given to the nu parameter of the OneClassSVM and the contamination parameter of the other outlier detection algorithms. Decision boundaries between inliers and outliers are displayed in black except for Local Outlier Factor (LOF) as it has no predict method to be applied on new data when it is used for outlier detection.
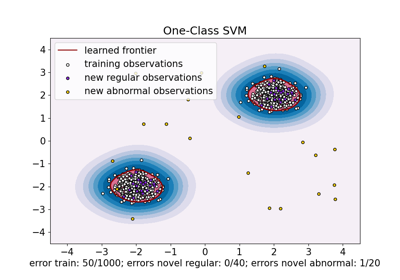
The OneClassSVM is known to be sensitive to outliers and
thus does not perform very well for outlier detection. This estimator is best
suited for novelty detection when the training set is not contaminated by
outliers. That said, outlier detection in high-dimension, or without any
assumptions on the distribution of the inlying data is very challenging, and a
One-class SVM might give useful results in these situations depending on the
value of its hyperparameters.
The sklearn.linear_model.SGDOneClassSVM is an implementation of the
One-Class SVM based on stochastic gradient descent (SGD). Combined with kernel
approximation, this estimator can be used to approximate the solution
of a kernelized sklearn.svm.OneClassSVM. We note that, although not
identical, the decision boundaries of the
sklearn.linear_model.SGDOneClassSVM and the ones of
sklearn.svm.OneClassSVM are very similar. The main advantage of using
sklearn.linear_model.SGDOneClassSVM is that it scales linearly with
the number of samples.
sklearn.covariance.EllipticEnvelope assumes the data is Gaussian and
learns an ellipse. It thus degrades when the data is not unimodal. Notice
however that this estimator is robust to outliers.
IsolationForest and
LocalOutlierFactor seem to perform reasonably well
for multi-modal data sets. The advantage of
LocalOutlierFactor over the other estimators is
shown for the third data set, where the two modes have different densities.
This advantage is explained by the local aspect of LOF, meaning that it only
compares the score of abnormality of one sample with the scores of its
neighbors.
Finally, for the last data set, it is hard to say that one sample is more
abnormal than another sample as they are uniformly distributed in a
hypercube. Except for the OneClassSVM which overfits a
little, all estimators present decent solutions for this situation. In such a
case, it would be wise to look more closely at the scores of abnormality of
the samples as a good estimator should assign similar scores to all the
samples.
While these examples give some intuition about the algorithms, this intuition might not apply to very high dimensional data.
Finally, note that parameters of the models have been here handpicked but that in practice they need to be adjusted. In the absence of labelled data, the problem is completely unsupervised so model selection can be a challenge.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import time
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs, make_moons
from sklearn.ensemble import IsolationForest
from sklearn.kernel_approximation import Nystroem
from sklearn.linear_model import SGDOneClassSVM
from sklearn.neighbors import LocalOutlierFactor
from sklearn.pipeline import make_pipeline
matplotlib.rcParams["contour.negative_linestyle"] = "solid"
# Example settings
n_samples = 300
outliers_fraction = 0.15
n_outliers = int(outliers_fraction * n_samples)
n_inliers = n_samples - n_outliers
# define outlier/anomaly detection methods to be compared.
# the SGDOneClassSVM must be used in a pipeline with a kernel approximation
# to give similar results to the OneClassSVM
anomaly_algorithms = [
(
"Robust covariance",
EllipticEnvelope(contamination=outliers_fraction, random_state=42),
),
("One-Class SVM", svm.OneClassSVM(nu=outliers_fraction, kernel="rbf", gamma=0.1)),
(
"One-Class SVM (SGD)",
make_pipeline(
Nystroem(gamma=0.1, random_state=42, n_components=150),
SGDOneClassSVM(
nu=outliers_fraction,
shuffle=True,
fit_intercept=True,
random_state=42,
tol=1e-6,
),
),
),
(
"Isolation Forest",
IsolationForest(contamination=outliers_fraction, random_state=42),
),
(
"Local Outlier Factor",
LocalOutlierFactor(n_neighbors=35, contamination=outliers_fraction),
),
]
# Define datasets
blobs_params = dict(random_state=0, n_samples=n_inliers, n_features=2)
datasets = [
make_blobs(centers=[[0, 0], [0, 0]], cluster_std=0.5, **blobs_params)[0],
make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[0.5, 0.5], **blobs_params)[0],
make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[1.5, 0.3], **blobs_params)[0],
4.0
* (
make_moons(n_samples=n_samples, noise=0.05, random_state=0)[0]
- np.array([0.5, 0.25])
),
14.0 * (np.random.RandomState(42).rand(n_samples, 2) - 0.5),
]
# Compare given classifiers under given settings
xx, yy = np.meshgrid(np.linspace(-7, 7, 150), np.linspace(-7, 7, 150))
plt.figure(figsize=(len(anomaly_algorithms) * 2 + 4, 12.5))
plt.subplots_adjust(
left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01
)
plot_num = 1
rng = np.random.RandomState(42)
for i_dataset, X in enumerate(datasets):
# Add outliers
X = np.concatenate([X, rng.uniform(low=-6, high=6, size=(n_outliers, 2))], axis=0)
for name, algorithm in anomaly_algorithms:
t0 = time.time()
algorithm.fit(X)
t1 = time.time()
plt.subplot(len(datasets), len(anomaly_algorithms), plot_num)
if i_dataset == 0:
plt.title(name, size=18)
# fit the data and tag outliers
if name == "Local Outlier Factor":
y_pred = algorithm.fit_predict(X)
else:
y_pred = algorithm.fit(X).predict(X)
# plot the levels lines and the points
if name != "Local Outlier Factor": # LOF does not implement predict
Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="black")
colors = np.array(["#377eb8", "#ff7f00"])
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[(y_pred + 1) // 2])
plt.xlim(-7, 7)
plt.ylim(-7, 7)
plt.xticks(())
plt.yticks(())
plt.text(
0.99,
0.01,
("%.2fs" % (t1 - t0)).lstrip("0"),
transform=plt.gca().transAxes,
size=15,
horizontalalignment="right",
)
plot_num += 1
plt.show()
Total running time of the script: (0 minutes 3.279 seconds)
Related examples
One-Class SVM versus One-Class SVM using Stochastic Gradient Descent