Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder.
Quantile regression#
This example illustrates how quantile regression can predict non-trivial conditional quantiles.
The left figure shows the case when the error distribution is normal, but has non-constant variance, i.e. with heteroscedasticity.
The right figure shows an example of an asymmetric error distribution, namely the Pareto distribution.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Dataset generation#
To illustrate the behaviour of quantile regression, we will generate two
synthetic datasets. The true generative random processes for both datasets
will be composed by the same expected value with a linear relationship with a
single feature x.
import numpy as np
rng = np.random.RandomState(42)
x = np.linspace(start=0, stop=10, num=100)
X = x[:, np.newaxis]
y_true_mean = 10 + 0.5 * x
We will create two subsequent problems by changing the distribution of the
target y while keeping the same expected value:
in the first case, a heteroscedastic Normal noise is added;
in the second case, an asymmetric Pareto noise is added.
y_normal = y_true_mean + rng.normal(loc=0, scale=0.5 + 0.5 * x, size=x.shape[0])
a = 5
y_pareto = y_true_mean + 10 * (rng.pareto(a, size=x.shape[0]) - 1 / (a - 1))
Let’s first visualize the datasets as well as the distribution of the
residuals y - mean(y).
import matplotlib.pyplot as plt
_, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 11), sharex="row", sharey="row")
axs[0, 0].plot(x, y_true_mean, label="True mean")
axs[0, 0].scatter(x, y_normal, color="black", alpha=0.5, label="Observations")
axs[1, 0].hist(y_true_mean - y_normal, edgecolor="black")
axs[0, 1].plot(x, y_true_mean, label="True mean")
axs[0, 1].scatter(x, y_pareto, color="black", alpha=0.5, label="Observations")
axs[1, 1].hist(y_true_mean - y_pareto, edgecolor="black")
axs[0, 0].set_title("Dataset with heteroscedastic Normal distributed targets")
axs[0, 1].set_title("Dataset with asymmetric Pareto distributed target")
axs[1, 0].set_title(
"Residuals distribution for heteroscedastic Normal distributed targets"
)
axs[1, 1].set_title("Residuals distribution for asymmetric Pareto distributed target")
axs[0, 0].legend()
axs[0, 1].legend()
axs[0, 0].set_ylabel("y")
axs[1, 0].set_ylabel("Counts")
axs[0, 1].set_xlabel("x")
axs[0, 0].set_xlabel("x")
axs[1, 0].set_xlabel("Residuals")
_ = axs[1, 1].set_xlabel("Residuals")
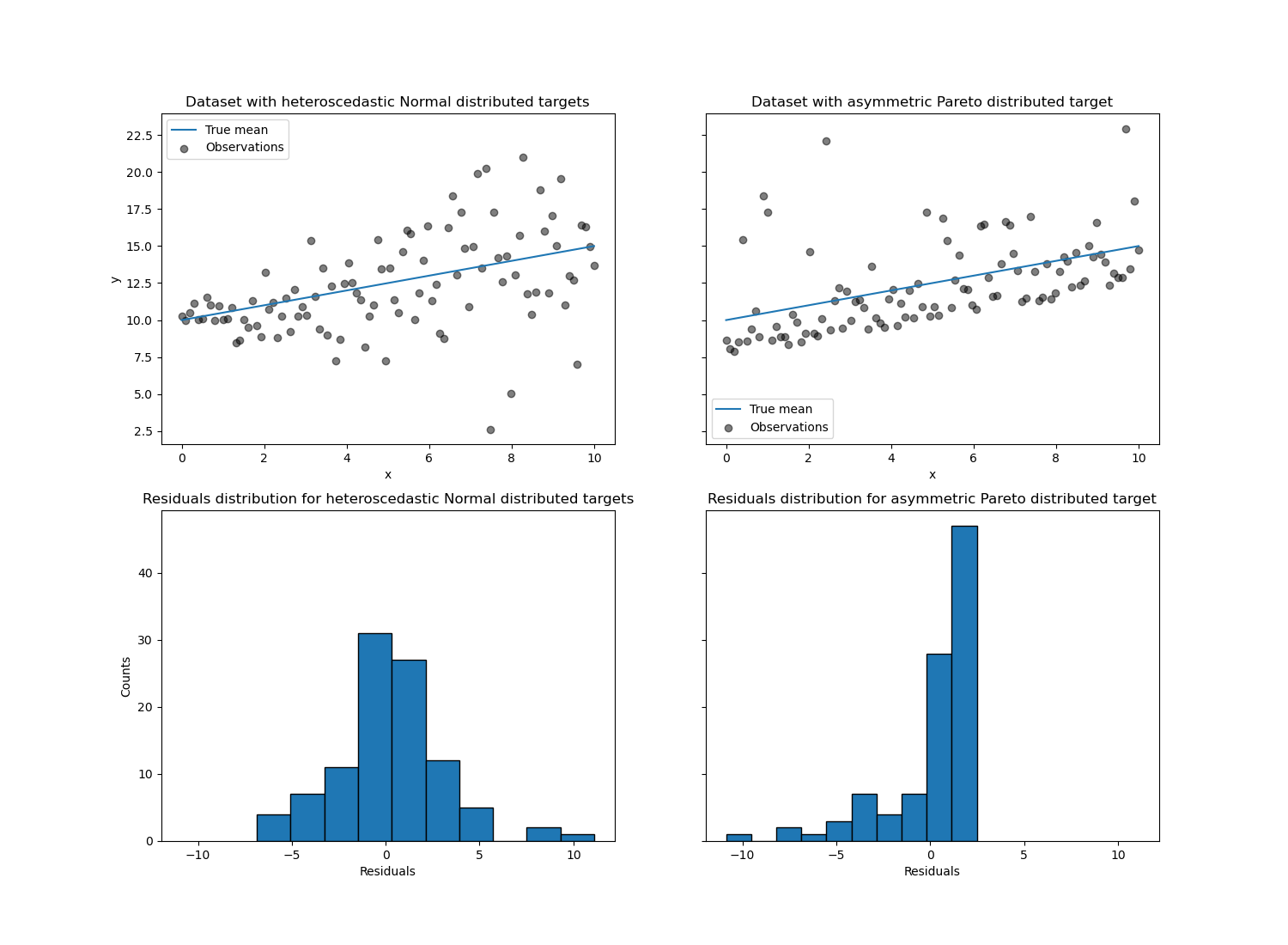
With the heteroscedastic Normal distributed target, we observe that the
variance of the noise is increasing when the value of the feature x is
increasing.
With the asymmetric Pareto distributed target, we observe that the positive residuals are bounded.
These types of noisy targets make the estimation via
LinearRegression less efficient, i.e. we need
more data to get stable results and, in addition, large outliers can have a
huge impact on the fitted coefficients. (Stated otherwise: in a setting with
constant variance, ordinary least squares estimators converge much faster to
the true coefficients with increasing sample size.)
In this asymmetric setting, the median or different quantiles give additional insights. On top of that, median estimation is much more robust to outliers and heavy tailed distributions. But note that extreme quantiles are estimated by very few data points. 95% quantile are more or less estimated by the 5% largest values and thus also a bit sensitive outliers.
In the remainder of this tutorial, we will show how
QuantileRegressor can be used in practice and
give the intuition into the properties of the fitted models. Finally,
we will compare the both QuantileRegressor
and LinearRegression.
Fitting a QuantileRegressor#
In this section, we want to estimate the conditional median as well as a low and high quantile fixed at 5% and 95%, respectively. Thus, we will get three linear models, one for each quantile.
We will use the quantiles at 5% and 95% to find the outliers in the training sample beyond the central 90% interval.
from sklearn.linear_model import QuantileRegressor
quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
qr = QuantileRegressor(quantile=quantile, alpha=0)
y_pred = qr.fit(X, y_normal).predict(X)
predictions[quantile] = y_pred
if quantile == min(quantiles):
out_bounds_predictions = np.logical_or(
out_bounds_predictions, y_pred >= y_normal
)
elif quantile == max(quantiles):
out_bounds_predictions = np.logical_or(
out_bounds_predictions, y_pred <= y_normal
)
Now, we can plot the three linear models and the distinguished samples that are within the central 90% interval from samples that are outside this interval.
plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="True mean")
for quantile, y_pred in predictions.items():
plt.plot(X, y_pred, label=f"Quantile: {quantile}")
plt.scatter(
x[out_bounds_predictions],
y_normal[out_bounds_predictions],
color="black",
marker="+",
alpha=0.5,
label="Outside interval",
)
plt.scatter(
x[~out_bounds_predictions],
y_normal[~out_bounds_predictions],
color="black",
alpha=0.5,
label="Inside interval",
)
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("Quantiles of heteroscedastic Normal distributed target")
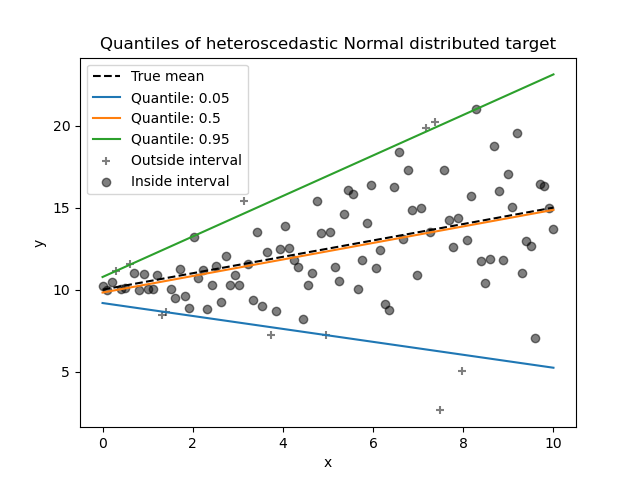
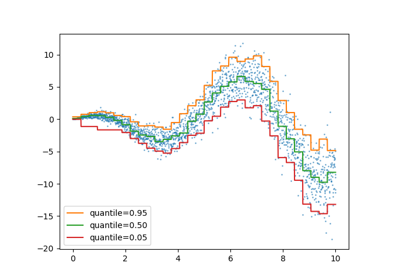
Since the noise is still Normally distributed, in particular is symmetric,
the true conditional mean and the true conditional median coincide. Indeed,
we see that the estimated median almost hits the true mean. We observe the
effect of having an increasing noise variance on the 5% and 95% quantiles:
the slopes of those quantiles are very different and the interval between
them becomes wider with increasing x.
To get an additional intuition regarding the meaning of the 5% and 95% quantiles estimators, one can count the number of samples above and below the predicted quantiles (represented by a cross on the above plot), considering that we have a total of 100 samples.
We can repeat the same experiment using the asymmetric Pareto distributed target.
quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
qr = QuantileRegressor(quantile=quantile, alpha=0)
y_pred = qr.fit(X, y_pareto).predict(X)
predictions[quantile] = y_pred
if quantile == min(quantiles):
out_bounds_predictions = np.logical_or(
out_bounds_predictions, y_pred >= y_pareto
)
elif quantile == max(quantiles):
out_bounds_predictions = np.logical_or(
out_bounds_predictions, y_pred <= y_pareto
)
plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="True mean")
for quantile, y_pred in predictions.items():
plt.plot(X, y_pred, label=f"Quantile: {quantile}")
plt.scatter(
x[out_bounds_predictions],
y_pareto[out_bounds_predictions],
color="black",
marker="+",
alpha=0.5,
label="Outside interval",
)
plt.scatter(
x[~out_bounds_predictions],
y_pareto[~out_bounds_predictions],
color="black",
alpha=0.5,
label="Inside interval",
)
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("Quantiles of asymmetric Pareto distributed target")
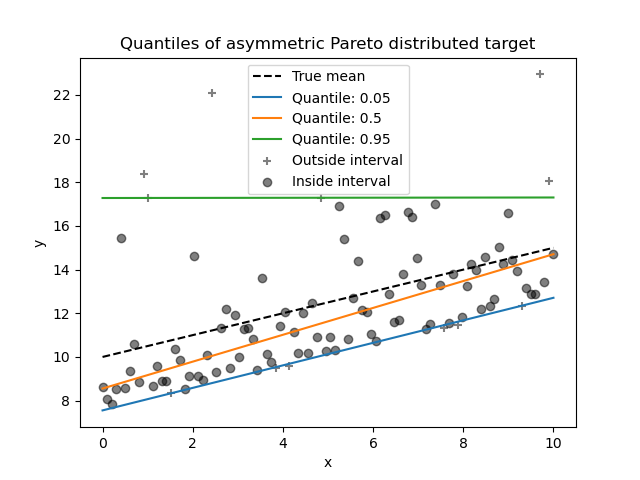
Due to the asymmetry of the distribution of the noise, we observe that the true mean and estimated conditional median are different. We also observe that each quantile model has different parameters to better fit the desired quantile. Note that ideally, all quantiles would be parallel in this case, which would become more visible with more data points or less extreme quantiles, e.g. 10% and 90%.
Comparing QuantileRegressor and LinearRegression#
In this section, we will linger on the difference regarding the loss functions that
QuantileRegressor and
LinearRegression are minimizing.
Indeed, LinearRegression is a least squares
approach minimizing the mean squared error (MSE) between the training and
predicted targets. In contrast,
QuantileRegressor with quantile=0.5
minimizes the mean absolute error (MAE) instead.
Why does it matter? The loss functions specify what exactly the model is aiming to predict, see user guide on the choice of scoring function. In short, a model minimizing MSE predicts the mean (expectation) and a model minimizing MAE predicts the median.
Let’s compute the training errors of such models in terms of mean squared error and mean absolute error. We will use the asymmetric Pareto distributed target to make it more interesting as mean and median are not equal.
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error
linear_regression = LinearRegression()
quantile_regression = QuantileRegressor(quantile=0.5, alpha=0)
y_pred_lr = linear_regression.fit(X, y_pareto).predict(X)
y_pred_qr = quantile_regression.fit(X, y_pareto).predict(X)
print(
"Training error (in-sample performance)\n"
f"{'model':<20} MAE MSE\n"
f"{linear_regression.__class__.__name__:<20} "
f"{mean_absolute_error(y_pareto, y_pred_lr):5.3f} "
f"{mean_squared_error(y_pareto, y_pred_lr):5.3f}\n"
f"{quantile_regression.__class__.__name__:<20} "
f"{mean_absolute_error(y_pareto, y_pred_qr):5.3f} "
f"{mean_squared_error(y_pareto, y_pred_qr):5.3f}"
)
Training error (in-sample performance)
model MAE MSE
LinearRegression 1.805 6.486
QuantileRegressor 1.670 7.025
On the training set, we see that MAE is lower for
QuantileRegressor than
LinearRegression. In contrast to that, MSE is
lower for LinearRegression than
QuantileRegressor. These results confirms that
MAE is the loss minimized by QuantileRegressor
while MSE is the loss minimized
LinearRegression.
We can make a similar evaluation by looking at the test error obtained by cross-validation.
from sklearn.model_selection import cross_validate
cv_results_lr = cross_validate(
linear_regression,
X,
y_pareto,
cv=3,
scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
cv_results_qr = cross_validate(
quantile_regression,
X,
y_pareto,
cv=3,
scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
print(
"Test error (cross-validated performance)\n"
f"{'model':<20} MAE MSE\n"
f"{linear_regression.__class__.__name__:<20} "
f"{-cv_results_lr['test_neg_mean_absolute_error'].mean():5.3f} "
f"{-cv_results_lr['test_neg_mean_squared_error'].mean():5.3f}\n"
f"{quantile_regression.__class__.__name__:<20} "
f"{-cv_results_qr['test_neg_mean_absolute_error'].mean():5.3f} "
f"{-cv_results_qr['test_neg_mean_squared_error'].mean():5.3f}"
)
Test error (cross-validated performance)
model MAE MSE
LinearRegression 1.732 6.690
QuantileRegressor 1.679 7.129
We reach similar conclusions on the out-of-sample evaluation.
Total running time of the script: (0 minutes 0.514 seconds)
Related examples
Prediction Intervals for Gradient Boosting Regression