Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder.
Feature importances with a forest of trees#
This example shows the use of a forest of trees to evaluate the importance of features on an artificial classification task. The blue bars are the feature importances of the forest, along with their inter-trees variability represented by the error bars.
As expected, the plot suggests that 3 features are informative, while the remaining are not.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
Data generation and model fitting#
We generate a synthetic dataset with only 3 informative features. We will explicitly not shuffle the dataset to ensure that the informative features will correspond to the three first columns of X. In addition, we will split our dataset into training and testing subsets.
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
X, y = make_classification(
n_samples=1000,
n_features=10,
n_informative=3,
n_redundant=0,
n_repeated=0,
n_classes=2,
random_state=0,
shuffle=False,
)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
A random forest classifier will be fitted to compute the feature importances.
from sklearn.ensemble import RandomForestClassifier
feature_names = [f"feature {i}" for i in range(X.shape[1])]
forest = RandomForestClassifier(random_state=0)
forest.fit(X_train, y_train)
Feature importance based on mean decrease in impurity#
Feature importances are provided by the fitted attribute
feature_importances_ and they are computed as the mean and standard
deviation of accumulation of the impurity decrease within each tree.
Warning
Impurity-based feature importances can be misleading for high cardinality features (many unique values). See Permutation feature importance as an alternative below.
Elapsed time to compute the importances: 0.018 seconds
Let’s plot the impurity-based importance.
import pandas as pd
forest_importances = pd.Series(importances, index=feature_names)
fig, ax = plt.subplots()
forest_importances.plot.bar(yerr=std, ax=ax)
ax.set_title("Feature importances using MDI")
ax.set_ylabel("Mean decrease in impurity")
fig.tight_layout()
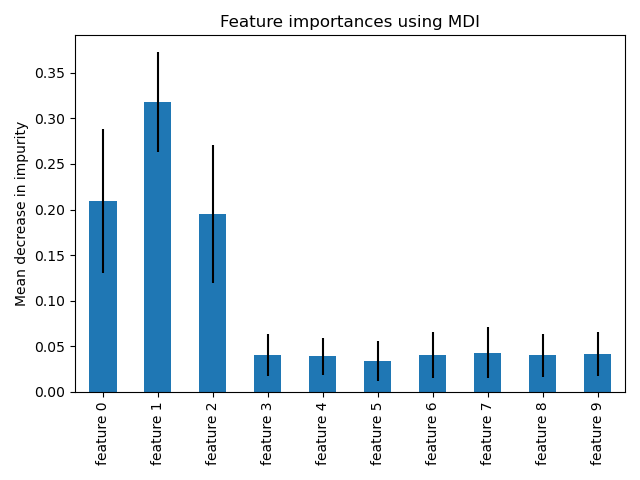
We observe that, as expected, the three first features are found important.
Feature importance based on feature permutation#
Permutation feature importance overcomes limitations of the impurity-based feature importance: they do not have a bias toward high-cardinality features and can be computed on a left-out test set.
from sklearn.inspection import permutation_importance
start_time = time.time()
result = permutation_importance(
forest, X_test, y_test, n_repeats=10, random_state=42, n_jobs=2
)
elapsed_time = time.time() - start_time
print(f"Elapsed time to compute the importances: {elapsed_time:.3f} seconds")
forest_importances = pd.Series(result.importances_mean, index=feature_names)
Elapsed time to compute the importances: 1.203 seconds
The computation for full permutation importance is more costly. Each feature is shuffled n times and the model is used to make predictions on the permuted data to see the drop in performance. Please see Permutation feature importance for more details. We can now plot the importance ranking.
fig, ax = plt.subplots()
forest_importances.plot.bar(yerr=result.importances_std, ax=ax)
ax.set_title("Feature importances using permutation on full model")
ax.set_ylabel("Mean accuracy decrease")
fig.tight_layout()
plt.show()
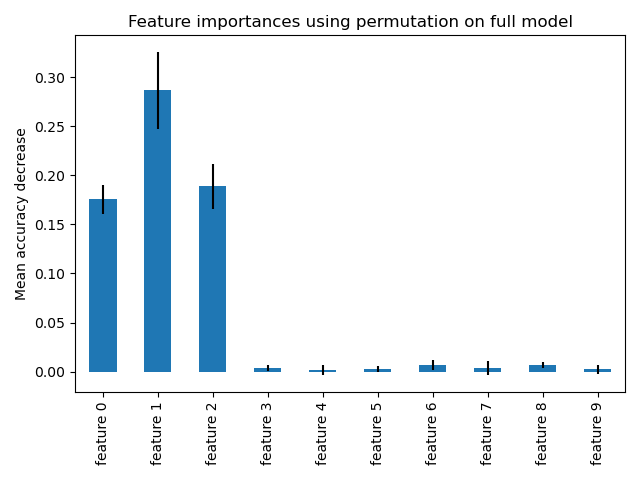
The same features are detected as most important using both methods. Although the relative importances vary. As seen on the plots, MDI is less likely than permutation importance to fully omit a feature.
Total running time of the script: (0 minutes 1.722 seconds)
Related examples
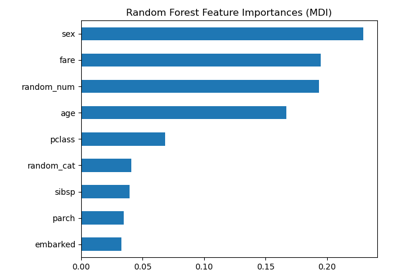
Permutation Importance vs Random Forest Feature Importance (MDI)
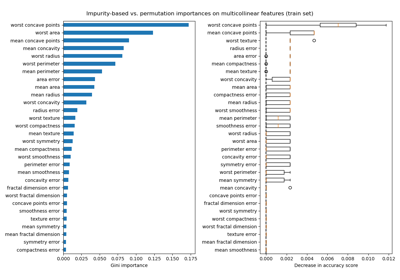
Permutation Importance with Multicollinear or Correlated Features