permutation_importance#
- sklearn.inspection.permutation_importance(estimator, X, y, *, scoring=None, n_repeats=5, n_jobs=None, random_state=None, sample_weight=None, max_samples=1.0)[source]#
Permutation importance for feature evaluation [BRE].
The estimator is required to be a fitted estimator.
Xcan be the data set used to train the estimator or a hold-out set. The permutation importance of a feature is calculated as follows. First, a baseline metric, defined by scoring, is evaluated on a (potentially different) dataset defined by theX. Next, a feature column from the validation set is permuted and the metric is evaluated again. The permutation importance is defined to be the difference between the baseline metric and metric from permutating the feature column.Read more in the User Guide.
- Parameters:
- estimatorobject
An estimator that has already been fitted and is compatible with scorer.
- Xndarray or DataFrame, shape (n_samples, n_features)
Data on which permutation importance will be computed.
- yarray-like or None, shape (n_samples, ) or (n_samples, n_classes)
Targets for supervised or
Nonefor unsupervised.- scoringstr, callable, list, tuple, or dict, default=None
Scorer to use. If
scoringrepresents a single score, one can use:str: see String name scorers for options.
callable: a scorer callable object (e.g., function) with signature
scorer(estimator, X, y). See Callable scorers for details.None: theestimator’s default evaluation criterion is used.
If
scoringrepresents multiple scores, one can use:a list or tuple of unique strings;
a callable returning a dictionary where the keys are the metric names and the values are the metric scores;
a dictionary with metric names as keys and callables a values.
Passing multiple scores to
scoringis more efficient than callingpermutation_importancefor each of the scores as it reuses predictions to avoid redundant computation.- n_repeatsint, default=5
Number of times to permute a feature.
- n_jobsint or None, default=None
Number of jobs to run in parallel. The computation is done by computing permutation score for each columns and parallelized over the columns.
Nonemeans 1 unless in ajoblib.parallel_backendcontext.-1means using all processors. See Glossary for more details.- random_stateint, RandomState instance, default=None
Pseudo-random number generator to control the permutations of each feature. Pass an int to get reproducible results across function calls. See Glossary.
- sample_weightarray-like of shape (n_samples,), default=None
Sample weights used in scoring.
Added in version 0.24.
- max_samplesint or float, default=1.0
The number of samples to draw from X to compute feature importance in each repeat (without replacement).
If int, then draw
max_samplessamples.If float, then draw
max_samples * X.shape[0]samples.If
max_samplesis equal to1.0orX.shape[0], all samples will be used.
While using this option may provide less accurate importance estimates, it keeps the method tractable when evaluating feature importance on large datasets. In combination with
n_repeats, this allows to control the computational speed vs statistical accuracy trade-off of this method.Added in version 1.0.
- Returns:
- result
Bunchor dict of such instances Dictionary-like object, with the following attributes.
- importances_meanndarray of shape (n_features, )
Mean of feature importance over
n_repeats.- importances_stdndarray of shape (n_features, )
Standard deviation over
n_repeats.- importancesndarray of shape (n_features, n_repeats)
Raw permutation importance scores.
If there are multiple scoring metrics in the scoring parameter
resultis a dict with scorer names as keys (e.g. ‘roc_auc’) andBunchobjects like above as values.
- result
References
Examples
>>> from sklearn.linear_model import LogisticRegression >>> from sklearn.inspection import permutation_importance >>> X = [[1, 9, 9],[1, 9, 9],[1, 9, 9], ... [0, 9, 9],[0, 9, 9],[0, 9, 9]] >>> y = [1, 1, 1, 0, 0, 0] >>> clf = LogisticRegression().fit(X, y) >>> result = permutation_importance(clf, X, y, n_repeats=10, ... random_state=0) >>> result.importances_mean array([0.4666, 0. , 0. ]) >>> result.importances_std array([0.2211, 0. , 0. ])
Gallery examples#
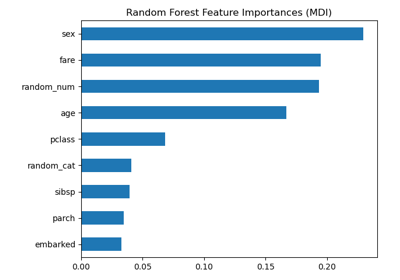
Permutation Importance vs Random Forest Feature Importance (MDI)
Permutation Importance with Multicollinear or Correlated Features