NMF#
- class sklearn.decomposition.NMF(n_components='auto', *, init=None, solver='cd', beta_loss='frobenius', tol=0.0001, max_iter=200, random_state=None, alpha_W=0.0, alpha_H='same', l1_ratio=0.0, verbose=0, shuffle=False)[source]#
Non-Negative Matrix Factorization (NMF).
Find two non-negative matrices, i.e. matrices with all non-negative elements, (W, H) whose product approximates the non-negative matrix X. This factorization can be used for example for dimensionality reduction, source separation or topic extraction.
The objective function is:
\[ \begin{align}\begin{aligned}L(W, H) &= 0.5 * ||X - WH||_{loss}^2\\ &+ alpha\_W * l1\_ratio * n\_features * ||vec(W)||_1\\ &+ alpha\_H * l1\_ratio * n\_samples * ||vec(H)||_1\\ &+ 0.5 * alpha\_W * (1 - l1\_ratio) * n\_features * ||W||_{Fro}^2\\ &+ 0.5 * alpha\_H * (1 - l1\_ratio) * n\_samples * ||H||_{Fro}^2,\end{aligned}\end{align} \]where \(||A||_{Fro}^2 = \sum_{i,j} A_{ij}^2\) (Frobenius norm) and \(||vec(A)||_1 = \sum_{i,j} abs(A_{ij})\) (Elementwise L1 norm).
The generic norm \(||X - WH||_{loss}\) may represent the Frobenius norm or another supported beta-divergence loss. The choice between options is controlled by the
beta_lossparameter.The regularization terms are scaled by
n_featuresforWand byn_samplesforHto keep their impact balanced with respect to one another and to the data fit term as independent as possible of the sizen_samplesof the training set.The objective function is minimized with an alternating minimization of W and H.
Note that the transformed data is named W and the components matrix is named H. In the NMF literature, the naming convention is usually the opposite since the data matrix X is transposed.
Read more in the User Guide.
- Parameters:
- n_componentsint or {‘auto’} or None, default=’auto’
Number of components. If
None, all features are kept. Ifn_components='auto', the number of components is automatically inferred from W or H shapes.Changed in version 1.4: Added
'auto'value.Changed in version 1.6: Default value changed from
Noneto'auto'.- init{‘random’, ‘nndsvd’, ‘nndsvda’, ‘nndsvdar’, ‘custom’}, default=None
Method used to initialize the procedure. Valid options:
None: ‘nndsvda’ if n_components <= min(n_samples, n_features), otherwise random.'random': non-negative random matrices, scaled with:sqrt(X.mean() / n_components)'nndsvd': Nonnegative Double Singular Value Decomposition (NNDSVD) initialization (better for sparseness)'nndsvda': NNDSVD with zeros filled with the average of X (better when sparsity is not desired)'nndsvdar'NNDSVD with zeros filled with small random values (generally faster, less accurate alternative to NNDSVDa for when sparsity is not desired)'custom': Use custom matricesWandHwhich must both be provided.
Changed in version 1.1: When
init=Noneand n_components is less than n_samples and n_features defaults tonndsvdainstead ofnndsvd.- solver{‘cd’, ‘mu’}, default=’cd’
Numerical solver to use:
‘cd’ is a Coordinate Descent solver.
‘mu’ is a Multiplicative Update solver.
Added in version 0.17: Coordinate Descent solver.
Added in version 0.19: Multiplicative Update solver.
- beta_lossfloat or {‘frobenius’, ‘kullback-leibler’, ‘itakura-saito’}, default=’frobenius’
Beta divergence to be minimized, measuring the distance between X and the dot product WH. Note that values different from ‘frobenius’ (or 2) and ‘kullback-leibler’ (or 1) lead to significantly slower fits. Note that for beta_loss <= 0 (or ‘itakura-saito’), the input matrix X cannot contain zeros. Used only in ‘mu’ solver.
Added in version 0.19.
- tolfloat, default=1e-4
Tolerance of the stopping condition.
- max_iterint, default=200
Maximum number of iterations before timing out.
- random_stateint, RandomState instance or None, default=None
Used for initialisation (when
init== ‘nndsvdar’ or ‘random’), and in Coordinate Descent. Pass an int for reproducible results across multiple function calls. See Glossary.- alpha_Wfloat, default=0.0
Constant that multiplies the regularization terms of
W. Set it to zero (default) to have no regularization onW.Added in version 1.0.
- alpha_Hfloat or “same”, default=”same”
Constant that multiplies the regularization terms of
H. Set it to zero to have no regularization onH. If “same” (default), it takes the same value asalpha_W.Added in version 1.0.
- l1_ratiofloat, default=0.0
The regularization mixing parameter, with 0 <= l1_ratio <= 1. For l1_ratio = 0 the penalty is an elementwise L2 penalty (aka Frobenius Norm). For l1_ratio = 1 it is an elementwise L1 penalty. For 0 < l1_ratio < 1, the penalty is a combination of L1 and L2.
Added in version 0.17: Regularization parameter l1_ratio used in the Coordinate Descent solver.
- verboseint, default=0
Whether to be verbose.
- shufflebool, default=False
If true, randomize the order of coordinates in the CD solver.
Added in version 0.17: shuffle parameter used in the Coordinate Descent solver.
- Attributes:
- components_ndarray of shape (n_components, n_features)
Factorization matrix, sometimes called ‘dictionary’.
- n_components_int
The number of components. It is same as the
n_componentsparameter if it was given. Otherwise, it will be same as the number of features.- reconstruction_err_float
Frobenius norm of the matrix difference, or beta-divergence, between the training data
Xand the reconstructed dataWHfrom the fitted model.- n_iter_int
Actual number of iterations.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
DictionaryLearningFind a dictionary that sparsely encodes data.
MiniBatchSparsePCAMini-batch Sparse Principal Components Analysis.
PCAPrincipal component analysis.
SparseCoderFind a sparse representation of data from a fixed, precomputed dictionary.
SparsePCASparse Principal Components Analysis.
TruncatedSVDDimensionality reduction using truncated SVD.
References
[1]“Fast local algorithms for large scale nonnegative matrix and tensor factorizations” Cichocki, Andrzej, and P. H. A. N. Anh-Huy. IEICE transactions on fundamentals of electronics, communications and computer sciences 92.3: 708-721, 2009.
[2]“Algorithms for nonnegative matrix factorization with the beta-divergence” Fevotte, C., & Idier, J. (2011). Neural Computation, 23(9).
Examples
>>> import numpy as np >>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]]) >>> from sklearn.decomposition import NMF >>> model = NMF(n_components=2, init='random', random_state=0) >>> W = model.fit_transform(X) >>> H = model.components_
- fit(X, y=None, **params)[source]#
Learn a NMF model for the data X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training vector, where
n_samplesis the number of samples andn_featuresis the number of features.- yIgnored
Not used, present for API consistency by convention.
- **paramskwargs
Parameters (keyword arguments) and values passed to the fit_transform instance.
- Returns:
- selfobject
Returns the instance itself.
- fit_transform(X, y=None, W=None, H=None)[source]#
Learn a NMF model for the data X and returns the transformed data.
This is more efficient than calling fit followed by transform.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training vector, where
n_samplesis the number of samples andn_featuresis the number of features.- yIgnored
Not used, present for API consistency by convention.
- Warray-like of shape (n_samples, n_components), default=None
If
init='custom', it is used as initial guess for the solution. IfNone, uses the initialisation method specified ininit.- Harray-like of shape (n_components, n_features), default=None
If
init='custom', it is used as initial guess for the solution. IfNone, uses the initialisation method specified ininit.
- Returns:
- Wndarray of shape (n_samples, n_components)
Transformed data.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are:
["class_name0", "class_name1", "class_name2"].- Parameters:
- input_featuresarray-like of str or None, default=None
Only used to validate feature names with the names seen in
fit.
- Returns:
- feature_names_outndarray of str objects
Transformed feature names.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- inverse_transform(X)[source]#
Transform data back to its original space.
Added in version 0.18.
- Parameters:
- X{ndarray, sparse matrix} of shape (n_samples, n_components)
Transformed data matrix.
- Returns:
- X_originalndarray of shape (n_samples, n_features)
Returns a data matrix of the original shape.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- transform(X)[source]#
Transform the data X according to the fitted NMF model.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training vector, where
n_samplesis the number of samples andn_featuresis the number of features.
- Returns:
- Wndarray of shape (n_samples, n_components)
Transformed data.
Gallery examples#
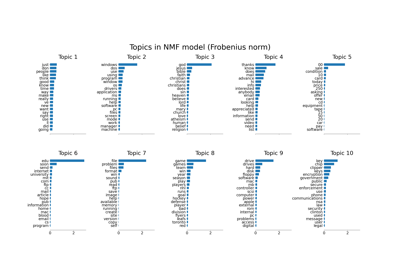
Topic extraction with Non-negative Matrix Factorization and Latent Dirichlet Allocation
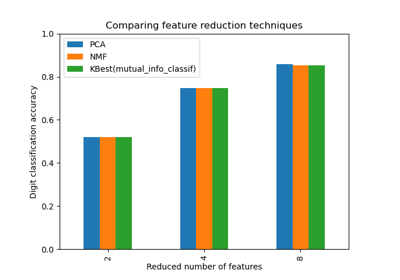
Selecting dimensionality reduction with Pipeline and GridSearchCV
