BayesianRidge#
- class sklearn.linear_model.BayesianRidge(*, max_iter=300, tol=0.001, alpha_1=1e-06, alpha_2=1e-06, lambda_1=1e-06, lambda_2=1e-06, alpha_init=None, lambda_init=None, compute_score=False, fit_intercept=True, copy_X=True, verbose=False)[source]#
Bayesian ridge regression.
Fit a Bayesian ridge model. See the Notes section for details on this implementation and the optimization of the regularization parameters lambda (precision of the weights) and alpha (precision of the noise).
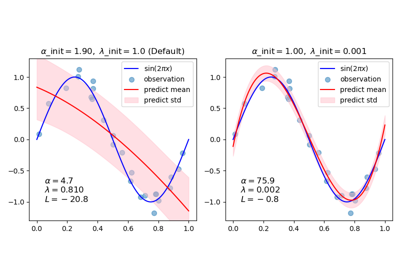
Read more in the User Guide. For an intuitive visualization of how the sinusoid is approximated by a polynomial using different pairs of initial values, see Curve Fitting with Bayesian Ridge Regression.
- Parameters:
- max_iterint, default=300
Maximum number of iterations over the complete dataset before stopping independently of any early stopping criterion.
Changed in version 1.3.
- tolfloat, default=1e-3
Stop the algorithm if w has converged.
- alpha_1float, default=1e-6
Hyper-parameter : shape parameter for the Gamma distribution prior over the alpha parameter.
- alpha_2float, default=1e-6
Hyper-parameter : inverse scale parameter (rate parameter) for the Gamma distribution prior over the alpha parameter.
- lambda_1float, default=1e-6
Hyper-parameter : shape parameter for the Gamma distribution prior over the lambda parameter.
- lambda_2float, default=1e-6
Hyper-parameter : inverse scale parameter (rate parameter) for the Gamma distribution prior over the lambda parameter.
- alpha_initfloat, default=None
Initial value for alpha (precision of the noise). If not set, alpha_init is 1/Var(y).
Added in version 0.22.
- lambda_initfloat, default=None
Initial value for lambda (precision of the weights). If not set, lambda_init is 1.
Added in version 0.22.
- compute_scorebool, default=False
If True, compute the log marginal likelihood at each iteration of the optimization.
- fit_interceptbool, default=True
Whether to calculate the intercept for this model. The intercept is not treated as a probabilistic parameter and thus has no associated variance. If set to False, no intercept will be used in calculations (i.e. data is expected to be centered).
- copy_Xbool, default=True
If True, X will be copied; else, it may be overwritten.
- verbosebool, default=False
Verbose mode when fitting the model.
- Attributes:
- coef_array-like of shape (n_features,)
Coefficients of the regression model (mean of distribution)
- intercept_float
Independent term in decision function. Set to 0.0 if
fit_intercept = False.- alpha_float
Estimated precision of the noise.
- lambda_float
Estimated precision of the weights.
- sigma_array-like of shape (n_features, n_features)
Estimated variance-covariance matrix of the weights
- scores_array-like of shape (n_iter_+1,)
If computed_score is True, value of the log marginal likelihood (to be maximized) at each iteration of the optimization. The array starts with the value of the log marginal likelihood obtained for the initial values of alpha and lambda and ends with the value obtained for the estimated alpha and lambda.
- n_iter_int
The actual number of iterations to reach the stopping criterion.
- X_offset_ndarray of shape (n_features,)
If
fit_intercept=True, offset subtracted for centering data to a zero mean. Set to np.zeros(n_features) otherwise.- X_scale_ndarray of shape (n_features,)
Set to np.ones(n_features).
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
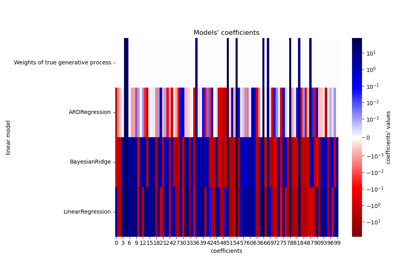
ARDRegressionBayesian ARD regression.
Notes
There exist several strategies to perform Bayesian ridge regression. This implementation is based on the algorithm described in Appendix A of (Tipping, 2001) where updates of the regularization parameters are done as suggested in (MacKay, 1992). Note that according to A New View of Automatic Relevance Determination (Wipf and Nagarajan, 2008) these update rules do not guarantee that the marginal likelihood is increasing between two consecutive iterations of the optimization.
References
D. J. C. MacKay, Bayesian Interpolation, Computation and Neural Systems, Vol. 4, No. 3, 1992.
M. E. Tipping, Sparse Bayesian Learning and the Relevance Vector Machine, Journal of Machine Learning Research, Vol. 1, 2001.
Examples
>>> from sklearn import linear_model >>> clf = linear_model.BayesianRidge() >>> clf.fit([[0,0], [1, 1], [2, 2]], [0, 1, 2]) BayesianRidge() >>> clf.predict([[1, 1]]) array([1.])
- fit(X, y, sample_weight=None)[source]#
Fit the model.
- Parameters:
- Xndarray of shape (n_samples, n_features)
Training data.
- yndarray of shape (n_samples,)
Target values. Will be cast to X’s dtype if necessary.
- sample_weightndarray of shape (n_samples,), default=None
Individual weights for each sample.
Added in version 0.20: parameter sample_weight support to BayesianRidge.
- Returns:
- selfobject
Returns the instance itself.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- predict(X, return_std=False)[source]#
Predict using the linear model.
In addition to the mean of the predictive distribution, also its standard deviation can be returned.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Samples.
- return_stdbool, default=False
Whether to return the standard deviation of posterior prediction.
- Returns:
- y_meanarray-like of shape (n_samples,)
Mean of predictive distribution of query points.
- y_stdarray-like of shape (n_samples,)
Standard deviation of predictive distribution of query points.
- score(X, y, sample_weight=None)[source]#
Return coefficient of determination on test data.
The coefficient of determination, \(R^2\), is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares
((y_true - y_pred)** 2).sum()and \(v\) is the total sum of squares((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value ofy, disregarding the input features, would get a \(R^2\) score of 0.0.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape
(n_samples, n_samples_fitted), wheren_samples_fittedis the number of samples used in the fitting for the estimator.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True values for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
\(R^2\) of
self.predict(X)w.r.t.y.
Notes
The \(R^2\) score used when calling
scoreon a regressor usesmultioutput='uniform_average'from version 0.23 to keep consistent with default value ofr2_score. This influences thescoremethod of all the multioutput regressors (except forMultiOutputRegressor).
- set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') BayesianRidge[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_predict_request(*, return_std: bool | None | str = '$UNCHANGED$') BayesianRidge[source]#
Configure whether metadata should be requested to be passed to the
predictmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed topredictif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it topredict.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- return_stdstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
return_stdparameter inpredict.
- Returns:
- selfobject
The updated object.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') BayesianRidge[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
Gallery examples#
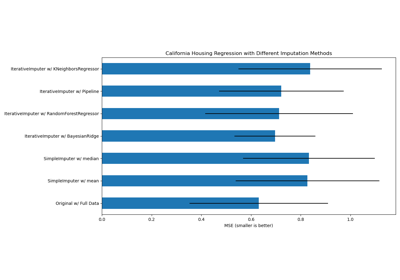
Imputing missing values with variants of IterativeImputer
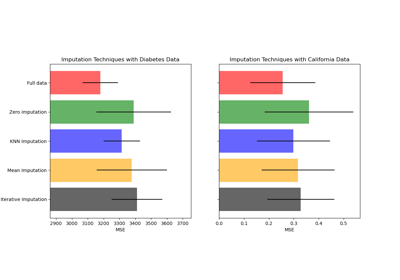
Imputing missing values before building an estimator