QuantileTransformer#
- class sklearn.preprocessing.QuantileTransformer(*, n_quantiles=1000, output_distribution='uniform', ignore_implicit_zeros=False, subsample=10000, random_state=None, copy=True)[source]#
Transform features using quantiles information.
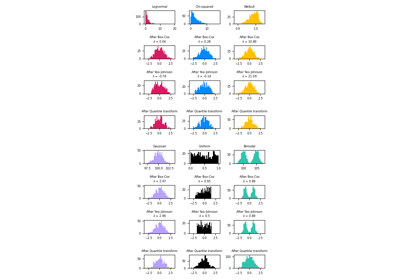
This method transforms the features to follow a uniform or a normal distribution. Therefore, for a given feature, this transformation tends to spread out the most frequent values. It also reduces the impact of (marginal) outliers: this is therefore a robust preprocessing scheme.
The transformation is applied on each feature independently. First an estimate of the cumulative distribution function of a feature is used to map the original values to a uniform distribution. The obtained values are then mapped to the desired output distribution using the associated quantile function. Features values of new/unseen data that fall below or above the fitted range will be mapped to the bounds of the output distribution. Note that this transform is non-linear. It may distort linear correlations between variables measured at the same scale but renders variables measured at different scales more directly comparable.
For example visualizations, refer to Compare QuantileTransformer with other scalers.
Read more in the User Guide.
Added in version 0.19.
- Parameters:
- n_quantilesint, default=1000 or n_samples
Number of quantiles to be computed. It corresponds to the number of landmarks used to discretize the cumulative distribution function. If n_quantiles is larger than the number of samples, n_quantiles is set to the number of samples as a larger number of quantiles does not give a better approximation of the cumulative distribution function estimator.
- output_distribution{‘uniform’, ‘normal’}, default=’uniform’
Marginal distribution for the transformed data. The choices are ‘uniform’ (default) or ‘normal’.
- ignore_implicit_zerosbool, default=False
Only applies to sparse matrices. If True, the sparse entries of the matrix are discarded to compute the quantile statistics. If False, these entries are treated as zeros.
- subsampleint or None, default=10_000
Maximum number of samples used to estimate the quantiles for computational efficiency. Note that the subsampling procedure may differ for value-identical sparse and dense matrices. Disable subsampling by setting
subsample=None.Added in version 1.5: The option
Noneto disable subsampling was added.- random_stateint, RandomState instance or None, default=None
Determines random number generation for subsampling and smoothing noise. Please see
subsamplefor more details. Pass an int for reproducible results across multiple function calls. See Glossary.- copybool, default=True
Set to False to perform inplace transformation and avoid a copy (if the input is already a numpy array).
- Attributes:
- n_quantiles_int
The actual number of quantiles used to discretize the cumulative distribution function.
- quantiles_ndarray of shape (n_quantiles, n_features)
The values corresponding the quantiles of reference.
- references_ndarray of shape (n_quantiles, )
Quantiles of references.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
quantile_transformEquivalent function without the estimator API.
PowerTransformerPerform mapping to a normal distribution using a power transform.
StandardScalerPerform standardization that is faster, but less robust to outliers.
RobustScalerPerform robust standardization that removes the influence of outliers but does not put outliers and inliers on the same scale.
Notes
NaNs are treated as missing values: disregarded in fit, and maintained in transform.
Examples
>>> import numpy as np >>> from sklearn.preprocessing import QuantileTransformer >>> rng = np.random.RandomState(0) >>> X = np.sort(rng.normal(loc=0.5, scale=0.25, size=(25, 1)), axis=0) >>> qt = QuantileTransformer(n_quantiles=10, random_state=0) >>> qt.fit_transform(X) array([...])
- fit(X, y=None)[source]#
Compute the quantiles used for transforming.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The data used to scale along the features axis. If a sparse matrix is provided, it will be converted into a sparse
csc_matrix. Additionally, the sparse matrix needs to be nonnegative ifignore_implicit_zerosis False.- yNone
Ignored.
- Returns:
- selfobject
Fitted transformer.
- fit_transform(X, y=None, **fit_params)[source]#
Fit to data, then transform it.
Fits transformer to
Xandywith optional parametersfit_paramsand returns a transformed version ofX.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Input samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None
Target values (None for unsupervised transformations).
- **fit_paramsdict
Additional fit parameters. Pass only if the estimator accepts additional params in its
fitmethod.
- Returns:
- X_newndarray array of shape (n_samples, n_features_new)
Transformed array.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
- Parameters:
- input_featuresarray-like of str or None, default=None
Input features.
If
input_featuresisNone, thenfeature_names_in_is used as feature names in. Iffeature_names_in_is not defined, then the following input feature names are generated:["x0", "x1", ..., "x(n_features_in_ - 1)"].If
input_featuresis an array-like, theninput_featuresmust matchfeature_names_in_iffeature_names_in_is defined.
- Returns:
- feature_names_outndarray of str objects
Same as input features.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- inverse_transform(X)[source]#
Back-projection to the original space.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The data used to scale along the features axis. If a sparse matrix is provided, it will be converted into a sparse
csc_matrix. Additionally, the sparse matrix needs to be nonnegative ifignore_implicit_zerosis False.
- Returns:
- X_original{ndarray, sparse matrix} of (n_samples, n_features)
The projected data.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- transform(X)[source]#
Feature-wise transformation of the data.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The data used to scale along the features axis. If a sparse matrix is provided, it will be converted into a sparse
csc_matrix. Additionally, the sparse matrix needs to be nonnegative ifignore_implicit_zerosis False.
- Returns:
- Xt{ndarray, sparse matrix} of shape (n_samples, n_features)
The projected data.
Gallery examples#
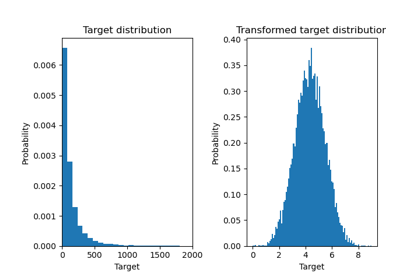
Effect of transforming the targets in regression model
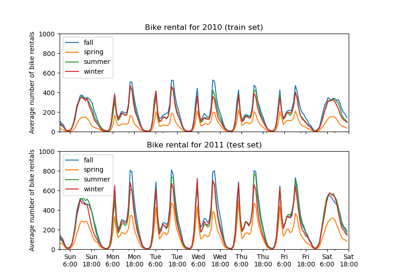
Partial Dependence and Individual Conditional Expectation Plots
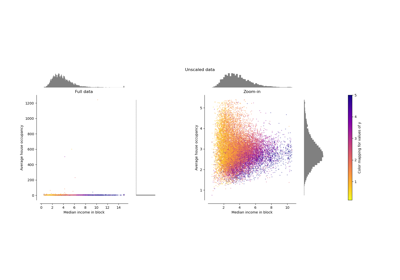
Compare the effect of different scalers on data with outliers