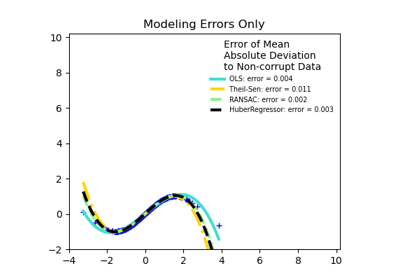
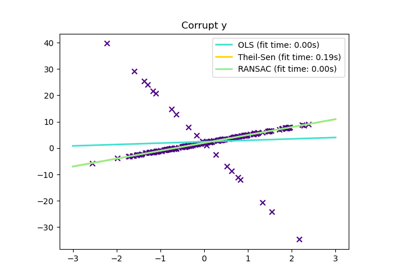
TheilSenRegressor#
- class sklearn.linear_model.TheilSenRegressor(*, fit_intercept=True, max_subpopulation=10000.0, n_subsamples=None, max_iter=300, tol=0.001, random_state=None, n_jobs=None, verbose=False)[source]#
Theil-Sen Estimator: robust multivariate regression model.
The algorithm calculates least square solutions on subsets with size n_subsamples of the samples in X. Any value of n_subsamples between the number of features and samples leads to an estimator with a compromise between robustness and efficiency. Since the number of least square solutions is “n_samples choose n_subsamples”, it can be extremely large and can therefore be limited with max_subpopulation. If this limit is reached, the subsets are chosen randomly. In a final step, the spatial median (or L1 median) is calculated of all least square solutions.
Read more in the User Guide.
- Parameters:
- fit_interceptbool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations.
- max_subpopulationint, default=1e4
Instead of computing with a set of cardinality ‘n choose k’, where n is the number of samples and k is the number of subsamples (at least number of features), consider only a stochastic subpopulation of a given maximal size if ‘n choose k’ is larger than max_subpopulation. For other than small problem sizes this parameter will determine memory usage and runtime if n_subsamples is not changed. Note that the data type should be int but floats such as 1e4 can be accepted too.
- n_subsamplesint, default=None
Number of samples to calculate the parameters. This is at least the number of features (plus 1 if fit_intercept=True) and the number of samples as a maximum. A lower number leads to a higher breakdown point and a low efficiency while a high number leads to a low breakdown point and a high efficiency. If None, take the minimum number of subsamples leading to maximal robustness. If n_subsamples is set to n_samples, Theil-Sen is identical to least squares.
- max_iterint, default=300
Maximum number of iterations for the calculation of spatial median.
- tolfloat, default=1e-3
Tolerance when calculating spatial median.
- random_stateint, RandomState instance or None, default=None
A random number generator instance to define the state of the random permutations generator. Pass an int for reproducible output across multiple function calls. See Glossary.
- n_jobsint, default=None
Number of CPUs to use during the cross validation.
Nonemeans 1 unless in ajoblib.parallel_backendcontext.-1means using all processors. See Glossary for more details.- verbosebool, default=False
Verbose mode when fitting the model.
- Attributes:
- coef_ndarray of shape (n_features,)
Coefficients of the regression model (median of distribution).
- intercept_float
Estimated intercept of regression model.
- breakdown_float
Approximated breakdown point.
- n_iter_int
Number of iterations needed for the spatial median.
- n_subpopulation_int
Number of combinations taken into account from ‘n choose k’, where n is the number of samples and k is the number of subsamples.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
HuberRegressorLinear regression model that is robust to outliers.
RANSACRegressorRANSAC (RANdom SAmple Consensus) algorithm.
SGDRegressorFitted by minimizing a regularized empirical loss with SGD.
References
Theil-Sen Estimators in a Multiple Linear Regression Model, 2009 Xin Dang, Hanxiang Peng, Xueqin Wang and Heping Zhang http://home.olemiss.edu/~xdang/papers/MTSE.pdf
Examples
>>> from sklearn.linear_model import TheilSenRegressor >>> from sklearn.datasets import make_regression >>> X, y = make_regression( ... n_samples=200, n_features=2, noise=4.0, random_state=0) >>> reg = TheilSenRegressor(random_state=0).fit(X, y) >>> reg.score(X, y) 0.9884 >>> reg.predict(X[:1,]) array([-31.5871])
- fit(X, y)[source]#
Fit linear model.
- Parameters:
- Xndarray of shape (n_samples, n_features)
Training data.
- yndarray of shape (n_samples,)
Target values.
- Returns:
- selfreturns an instance of self.
Fitted
TheilSenRegressorestimator.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- predict(X)[source]#
Predict using the linear model.
- Parameters:
- Xarray-like or sparse matrix, shape (n_samples, n_features)
Samples.
- Returns:
- Carray, shape (n_samples,)
Returns predicted values.
- score(X, y, sample_weight=None)[source]#
Return coefficient of determination on test data.
The coefficient of determination, \(R^2\), is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares
((y_true - y_pred)** 2).sum()and \(v\) is the total sum of squares((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value ofy, disregarding the input features, would get a \(R^2\) score of 0.0.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape
(n_samples, n_samples_fitted), wheren_samples_fittedis the number of samples used in the fitting for the estimator.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True values for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
\(R^2\) of
self.predict(X)w.r.t.y.
Notes
The \(R^2\) score used when calling
scoreon a regressor usesmultioutput='uniform_average'from version 0.23 to keep consistent with default value ofr2_score. This influences thescoremethod of all the multioutput regressors (except forMultiOutputRegressor).
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') TheilSenRegressor[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.