johnson_lindenstrauss_min_dim#
- sklearn.random_projection.johnson_lindenstrauss_min_dim(n_samples, *, eps=0.1)[source]#
Find a ‘safe’ number of components to randomly project to.
The distortion introduced by a random projection
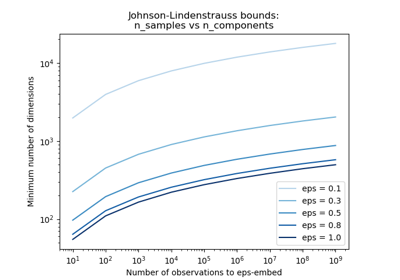
ponly changes the distance between two points by a factor (1 +- eps) in a euclidean space with good probability. The projectionpis an eps-embedding as defined by:(1 - eps) ||u - v||^2 < ||p(u) - p(v)||^2 < (1 + eps) ||u - v||^2
Where u and v are any rows taken from a dataset of shape (n_samples, n_features), eps is in ]0, 1[ and p is a projection by a random Gaussian N(0, 1) matrix of shape (n_components, n_features) (or a sparse Achlioptas matrix).
The minimum number of components to guarantee the eps-embedding is given by:
n_components >= 4 log(n_samples) / (eps^2 / 2 - eps^3 / 3)
Note that the number of dimensions is independent of the original number of features but instead depends on the size of the dataset: the larger the dataset, the higher is the minimal dimensionality of an eps-embedding.
Read more in the User Guide.
- Parameters:
- n_samplesint or array-like of int
Number of samples that should be an integer greater than 0. If an array is given, it will compute a safe number of components array-wise.
- epsfloat or array-like of shape (n_components,), dtype=float, default=0.1
Maximum distortion rate in the range (0, 1) as defined by the Johnson-Lindenstrauss lemma. If an array is given, it will compute a safe number of components array-wise.
- Returns:
- n_componentsint or ndarray of int
The minimal number of components to guarantee with good probability an eps-embedding with n_samples.
References
Examples
>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim >>> johnson_lindenstrauss_min_dim(1e6, eps=0.5) np.int64(663)
>>> johnson_lindenstrauss_min_dim(1e6, eps=[0.5, 0.1, 0.01]) array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim([1e4, 1e5, 1e6], eps=0.1) array([ 7894, 9868, 11841])
Gallery examples#
The Johnson-Lindenstrauss bound for embedding with random projections