ExtraTreesClassifier#
- class sklearn.ensemble.ExtraTreesClassifier(n_estimators=100, *, criterion='gini', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features='sqrt', max_leaf_nodes=None, min_impurity_decrease=0.0, bootstrap=False, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None, ccp_alpha=0.0, max_samples=None, monotonic_cst=None)[source]#
An extra-trees classifier.
This class implements a meta estimator that fits a number of randomized decision trees (a.k.a. extra-trees) on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting.
This estimator has native support for missing values (NaNs) for random splits. During training, a random threshold will be chosen to split the non-missing values on. Then the non-missing values will be sent to the left and right child based on the randomly selected threshold, while the missing values will also be randomly sent to the left or right child. This is repeated for every feature considered at each split. The best split among these is chosen.
Read more in the User Guide.
- Parameters:
- n_estimatorsint, default=100
The number of trees in the forest.
Changed in version 0.22: The default value of
n_estimatorschanged from 10 to 100 in 0.22.- criterion{“gini”, “entropy”, “log_loss”}, default=”gini”
The function to measure the quality of a split. Supported criteria are “gini” for the Gini impurity and “log_loss” and “entropy” both for the Shannon information gain, see Mathematical formulation. Note: This parameter is tree-specific.
- max_depthint, default=None
The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min_samples_split samples.
- min_samples_splitint or float, default=2
The minimum number of samples required to split an internal node:
If int, then consider
min_samples_splitas the minimum number.If float, then
min_samples_splitis a fraction andceil(min_samples_split * n_samples)are the minimum number of samples for each split.
Changed in version 0.18: Added float values for fractions.
- min_samples_leafint or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least
min_samples_leaftraining samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.If int, then consider
min_samples_leafas the minimum number.If float, then
min_samples_leafis a fraction andceil(min_samples_leaf * n_samples)are the minimum number of samples for each node.
Changed in version 0.18: Added float values for fractions.
- min_weight_fraction_leaffloat, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample_weight is not provided.
- max_features{“sqrt”, “log2”, None}, int or float, default=”sqrt”
The number of features to consider when looking for the best split:
If int, then consider
max_featuresfeatures at each split.If float, then
max_featuresis a fraction andmax(1, int(max_features * n_features_in_))features are considered at each split.If “sqrt”, then
max_features=sqrt(n_features).If “log2”, then
max_features=log2(n_features).If None, then
max_features=n_features.
Changed in version 1.1: The default of
max_featureschanged from"auto"to"sqrt".Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than
max_featuresfeatures.- max_leaf_nodesint, default=None
Grow trees with
max_leaf_nodesin best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.- min_impurity_decreasefloat, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.
The weighted impurity decrease equation is the following:
N_t / N * (impurity - N_t_R / N_t * right_impurity - N_t_L / N_t * left_impurity)
where
Nis the total number of samples,N_tis the number of samples at the current node,N_t_Lis the number of samples in the left child, andN_t_Ris the number of samples in the right child.N,N_t,N_t_RandN_t_Lall refer to the weighted sum, ifsample_weightis passed.Added in version 0.19.
- bootstrapbool, default=False
Whether bootstrap samples are used when building trees. If False, the whole dataset is used to build each tree.
- oob_scorebool or callable, default=False
Whether to use out-of-bag samples to estimate the generalization score. By default,
accuracy_scoreis used. Provide a callable with signaturemetric(y_true, y_pred)to use a custom metric. Only available ifbootstrap=True.For an illustration of out-of-bag (OOB) error estimation, see the example OOB Errors for Random Forests.
- n_jobsint, default=None
The number of jobs to run in parallel.
fit,predict,decision_pathandapplyare all parallelized over the trees.Nonemeans 1 unless in ajoblib.parallel_backendcontext.-1means using all processors. See Glossary for more details.- random_stateint, RandomState instance or None, default=None
Controls 3 sources of randomness:
the bootstrapping of the samples used when building trees (if
bootstrap=True)the sampling of the features to consider when looking for the best split at each node (if
max_features < n_features)the draw of the splits for each of the
max_features
See Glossary for details.
- verboseint, default=0
Controls the verbosity when fitting and predicting.
- warm_startbool, default=False
When set to
True, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just fit a whole new forest. See Glossary and Fitting additional trees for details.- class_weight{“balanced”, “balanced_subsample”}, dict or list of dicts, default=None
Weights associated with classes in the form
{class_label: weight}. If not given, all classes are supposed to have weight one. For multi-output problems, a list of dicts can be provided in the same order as the columns of y.Note that for multioutput (including multilabel) weights should be defined for each class of every column in its own dict. For example, for four-class multilabel classification weights should be [{0: 1, 1: 1}, {0: 1, 1: 5}, {0: 1, 1: 1}, {0: 1, 1: 1}] instead of [{1:1}, {2:5}, {3:1}, {4:1}].
The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as
n_samples / (n_classes * np.bincount(y))The “balanced_subsample” mode is the same as “balanced” except that weights are computed based on the bootstrap sample for every tree grown.
For multi-output, the weights of each column of y will be multiplied.
Note that these weights will be multiplied with sample_weight (passed through the fit method) if sample_weight is specified.
- ccp_alphanon-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than
ccp_alphawill be chosen. By default, no pruning is performed. See Minimal Cost-Complexity Pruning for details. See Post pruning decision trees with cost complexity pruning for an example of such pruning.Added in version 0.22.
- max_samplesint or float, default=None
If bootstrap is True, the number of samples to draw from X to train each base estimator.
If None (default), then draw
X.shape[0]samples.If int, then draw
max_samplessamples.If float, then draw
max_samples * X.shape[0]samples. Thus,max_samplesshould be in the interval(0.0, 1.0].
Added in version 0.22.
- monotonic_cstarray-like of int of shape (n_features), default=None
- Indicates the monotonicity constraint to enforce on each feature.
1: monotonically increasing
0: no constraint
-1: monotonically decreasing
If monotonic_cst is None, no constraints are applied.
- Monotonicity constraints are not supported for:
multiclass classifications (i.e. when
n_classes > 2),multioutput classifications (i.e. when
n_outputs_ > 1),classifications trained on data with missing values.
The constraints hold over the probability of the positive class.
Read more in the User Guide.
Added in version 1.4.
- Attributes:
- estimator_
ExtraTreeClassifier The child estimator template used to create the collection of fitted sub-estimators.
Added in version 1.2:
base_estimator_was renamed toestimator_.- estimators_list of DecisionTreeClassifier
The collection of fitted sub-estimators.
- classes_ndarray of shape (n_classes,) or a list of such arrays
The classes labels (single output problem), or a list of arrays of class labels (multi-output problem).
- n_classes_int or list
The number of classes (single output problem), or a list containing the number of classes for each output (multi-output problem).
feature_importances_ndarray of shape (n_features,)The impurity-based feature importances.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
- n_outputs_int
The number of outputs when
fitis performed.- oob_score_float
Score of the training dataset obtained using an out-of-bag estimate. This attribute exists only when
oob_scoreis True.- oob_decision_function_ndarray of shape (n_samples, n_classes) or (n_samples, n_classes, n_outputs)
Decision function computed with out-of-bag estimate on the training set. If n_estimators is small it might be possible that a data point was never left out during the bootstrap. In this case,
oob_decision_function_might contain NaN. This attribute exists only whenoob_scoreis True.estimators_samples_list of arraysThe subset of drawn samples for each base estimator.
- estimator_
See also
ExtraTreesRegressorAn extra-trees regressor with random splits.
RandomForestClassifierA random forest classifier with optimal splits.
RandomForestRegressorEnsemble regressor using trees with optimal splits.
Notes
The default values for the parameters controlling the size of the trees (e.g.
max_depth,min_samples_leaf, etc.) lead to fully grown and unpruned trees which can potentially be very large on some data sets. To reduce memory consumption, the complexity and size of the trees should be controlled by setting those parameter values.References
[1]P. Geurts, D. Ernst., and L. Wehenkel, “Extremely randomized trees”, Machine Learning, 63(1), 3-42, 2006.
Examples
>>> from sklearn.ensemble import ExtraTreesClassifier >>> from sklearn.datasets import make_classification >>> X, y = make_classification(n_features=4, random_state=0) >>> clf = ExtraTreesClassifier(n_estimators=100, random_state=0) >>> clf.fit(X, y) ExtraTreesClassifier(random_state=0) >>> clf.predict([[0, 0, 0, 0]]) array([1])
- apply(X)[source]#
Apply trees in the forest to X, return leaf indices.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, its dtype will be converted to
dtype=np.float32. If a sparse matrix is provided, it will be converted into a sparsecsr_matrix.
- Returns:
- X_leavesndarray of shape (n_samples, n_estimators)
For each datapoint x in X and for each tree in the forest, return the index of the leaf x ends up in.
- decision_path(X)[source]#
Return the decision path in the forest.
Added in version 0.18.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, its dtype will be converted to
dtype=np.float32. If a sparse matrix is provided, it will be converted into a sparsecsr_matrix.
- Returns:
- indicatorsparse matrix of shape (n_samples, n_nodes)
Return a node indicator matrix where non zero elements indicates that the samples goes through the nodes. The matrix is of CSR format.
- n_nodes_ptrndarray of shape (n_estimators + 1,)
The columns from indicator[n_nodes_ptr[i]:n_nodes_ptr[i+1]] gives the indicator value for the i-th estimator.
- fit(X, y, sample_weight=None)[source]#
Build a forest of trees from the training set (X, y).
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The training input samples. Internally, its dtype will be converted to
dtype=np.float32. If a sparse matrix is provided, it will be converted into a sparsecsc_matrix.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
The target values (class labels in classification, real numbers in regression).
- sample_weightarray-like of shape (n_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. In the case of classification, splits are also ignored if they would result in any single class carrying a negative weight in either child node.
- Returns:
- selfobject
Fitted estimator.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- predict(X)[source]#
Predict class for X.
The predicted class of an input sample is a vote by the trees in the forest, weighted by their probability estimates. That is, the predicted class is the one with highest mean probability estimate across the trees.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, its dtype will be converted to
dtype=np.float32. If a sparse matrix is provided, it will be converted into a sparsecsr_matrix.
- Returns:
- yndarray of shape (n_samples,) or (n_samples, n_outputs)
The predicted classes.
- predict_log_proba(X)[source]#
Predict class log-probabilities for X.
The predicted class log-probabilities of an input sample is computed as the log of the mean predicted class probabilities of the trees in the forest.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, its dtype will be converted to
dtype=np.float32. If a sparse matrix is provided, it will be converted into a sparsecsr_matrix.
- Returns:
- pndarray of shape (n_samples, n_classes), or a list of such arrays
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute classes_.
- predict_proba(X)[source]#
Predict class probabilities for X.
The predicted class probabilities of an input sample are computed as the mean predicted class probabilities of the trees in the forest. The class probability of a single tree is the fraction of samples of the same class in a leaf.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, its dtype will be converted to
dtype=np.float32. If a sparse matrix is provided, it will be converted into a sparsecsr_matrix.
- Returns:
- pndarray of shape (n_samples, n_classes), or a list of such arrays
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute classes_.
- score(X, y, sample_weight=None)[source]#
Return accuracy on provided data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True labels for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
Mean accuracy of
self.predict(X)w.r.t.y.
- set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') ExtraTreesClassifier[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') ExtraTreesClassifier[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
Gallery examples#
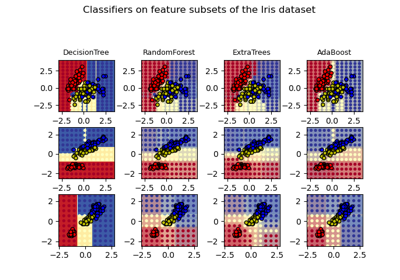
Plot the decision surfaces of ensembles of trees on the iris dataset
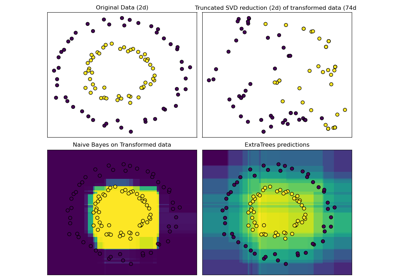
Hashing feature transformation using Totally Random Trees
