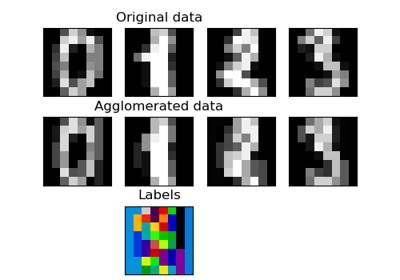
FeatureAgglomeration#
- class sklearn.cluster.FeatureAgglomeration(n_clusters=2, *, metric='euclidean', memory=None, connectivity=None, compute_full_tree='auto', linkage='ward', pooling_func=<function mean>, distance_threshold=None, compute_distances=False)[source]#
Agglomerate features.
Recursively merges pair of clusters of features.
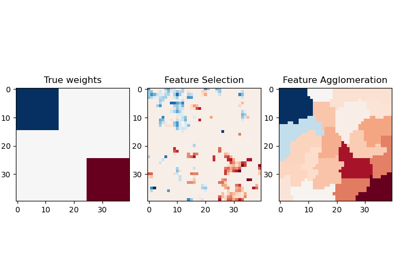
Refer to Feature agglomeration vs. univariate selection for an example comparison of
FeatureAgglomerationstrategy with a univariate feature selection strategy (based on ANOVA).Read more in the User Guide.
- Parameters:
- n_clustersint or None, default=2
The number of clusters to find. It must be
Noneifdistance_thresholdis notNone.- metricstr or callable, default=”euclidean”
Metric used to compute the linkage. Can be “euclidean”, “l1”, “l2”, “manhattan”, “cosine”, or “precomputed”. If linkage is “ward”, only “euclidean” is accepted. If “precomputed”, a distance matrix is needed as input for the fit method.
Added in version 1.2.
- memorystr or object with the joblib.Memory interface, default=None
Used to cache the output of the computation of the tree. By default, no caching is done. If a string is given, it is the path to the caching directory.
- connectivityarray-like, sparse matrix, or callable, default=None
Connectivity matrix. Defines for each feature the neighboring features following a given structure of the data. This can be a connectivity matrix itself or a callable that transforms the data into a connectivity matrix, such as derived from
kneighbors_graph. Default isNone, i.e, the hierarchical clustering algorithm is unstructured.- compute_full_tree‘auto’ or bool, default=’auto’
Stop early the construction of the tree at
n_clusters. This is useful to decrease computation time if the number of clusters is not small compared to the number of features. This option is useful only when specifying a connectivity matrix. Note also that when varying the number of clusters and using caching, it may be advantageous to compute the full tree. It must beTrueifdistance_thresholdis notNone. By defaultcompute_full_treeis “auto”, which is equivalent toTruewhendistance_thresholdis notNoneor thatn_clustersis inferior to the maximum between 100 or0.02 * n_samples. Otherwise, “auto” is equivalent toFalse.- linkage{“ward”, “complete”, “average”, “single”}, default=”ward”
Which linkage criterion to use. The linkage criterion determines which distance to use between sets of features. The algorithm will merge the pairs of cluster that minimize this criterion.
“ward” minimizes the variance of the clusters being merged.
“complete” or maximum linkage uses the maximum distances between all features of the two sets.
“average” uses the average of the distances of each feature of the two sets.
“single” uses the minimum of the distances between all features of the two sets.
- pooling_funccallable, default=np.mean
This combines the values of agglomerated features into a single value, and should accept an array of shape [M, N] and the keyword argument
axis=1, and reduce it to an array of size [M].- distance_thresholdfloat, default=None
The linkage distance threshold at or above which clusters will not be merged. If not
None,n_clustersmust beNoneandcompute_full_treemust beTrue.Added in version 0.21.
- compute_distancesbool, default=False
Computes distances between clusters even if
distance_thresholdis not used. This can be used to make dendrogram visualization, but introduces a computational and memory overhead.Added in version 0.24.
- Attributes:
- n_clusters_int
The number of clusters found by the algorithm. If
distance_threshold=None, it will be equal to the givenn_clusters.- labels_array-like of (n_features,)
Cluster labels for each feature.
- n_leaves_int
Number of leaves in the hierarchical tree.
- n_connected_components_int
The estimated number of connected components in the graph.
Added in version 0.21:
n_connected_components_was added to replacen_components_.- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
- children_array-like of shape (n_nodes-1, 2)
The children of each non-leaf node. Values less than
n_featurescorrespond to leaves of the tree which are the original samples. A nodeigreater than or equal ton_featuresis a non-leaf node and has childrenchildren_[i - n_features]. Alternatively at the i-th iteration, children[i][0] and children[i][1] are merged to form noden_features + i.- distances_array-like of shape (n_nodes-1,)
Distances between nodes in the corresponding place in
children_. Only computed ifdistance_thresholdis used orcompute_distancesis set toTrue.
See also
AgglomerativeClusteringAgglomerative clustering samples instead of features.
ward_treeHierarchical clustering with ward linkage.
Examples
>>> import numpy as np >>> from sklearn import datasets, cluster >>> digits = datasets.load_digits() >>> images = digits.images >>> X = np.reshape(images, (len(images), -1)) >>> agglo = cluster.FeatureAgglomeration(n_clusters=32) >>> agglo.fit(X) FeatureAgglomeration(n_clusters=32) >>> X_reduced = agglo.transform(X) >>> X_reduced.shape (1797, 32)
- fit(X, y=None)[source]#
Fit the hierarchical clustering on the data.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The data.
- yIgnored
Not used, present here for API consistency by convention.
- Returns:
- selfobject
Returns the transformer.
- property fit_predict#
Fit and return the result of each sample’s clustering assignment.
- fit_transform(X, y=None, **fit_params)[source]#
Fit to data, then transform it.
Fits transformer to
Xandywith optional parametersfit_paramsand returns a transformed version ofX.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Input samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None
Target values (None for unsupervised transformations).
- **fit_paramsdict
Additional fit parameters. Pass only if the estimator accepts additional params in its
fitmethod.
- Returns:
- X_newndarray array of shape (n_samples, n_features_new)
Transformed array.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are:
["class_name0", "class_name1", "class_name2"].- Parameters:
- input_featuresarray-like of str or None, default=None
Only used to validate feature names with the names seen in
fit.
- Returns:
- feature_names_outndarray of str objects
Transformed feature names.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- inverse_transform(X)[source]#
Inverse the transformation and return a vector of size
n_features.- Parameters:
- Xarray-like of shape (n_samples, n_clusters) or (n_clusters,)
The values to be assigned to each cluster of samples.
- Returns:
- X_originalndarray of shape (n_samples, n_features) or (n_features,)
A vector of size
n_sampleswith the values ofXassigned to each of the cluster of samples.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- transform(X)[source]#
Transform a new matrix using the built clustering.
- Parameters:
- Xarray-like of shape (n_samples, n_features) or (n_samples, n_samples)
An M by N array of M observations in N dimensions or a length M array of M one-dimensional observations.
- Returns:
- Yndarray of shape (n_samples, n_clusters) or (n_clusters,)
The pooled values for each feature cluster.