GradientBoostingClassifier#
- class sklearn.ensemble.GradientBoostingClassifier(*, loss='log_loss', learning_rate=0.1, n_estimators=100, subsample=1.0, criterion='friedman_mse', min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, init=None, random_state=None, max_features=None, verbose=0, max_leaf_nodes=None, warm_start=False, validation_fraction=0.1, n_iter_no_change=None, tol=0.0001, ccp_alpha=0.0)[source]#
Gradient Boosting for classification.
This algorithm builds an additive model in a forward stage-wise fashion; it allows for the optimization of arbitrary differentiable loss functions. In each stage
n_classes_regression trees are fit on the negative gradient of the loss function, e.g. binary or multiclass log loss. Binary classification is a special case where only a single regression tree is induced.HistGradientBoostingClassifieris a much faster variant of this algorithm for intermediate and large datasets (n_samples >= 10_000) and supports monotonic constraints.Read more in the User Guide.
- Parameters:
- loss{‘log_loss’, ‘exponential’}, default=’log_loss’
The loss function to be optimized. ‘log_loss’ refers to binomial and multinomial deviance, the same as used in logistic regression. It is a good choice for classification with probabilistic outputs. For loss ‘exponential’, gradient boosting recovers the AdaBoost algorithm.
- learning_ratefloat, default=0.1
Learning rate shrinks the contribution of each tree by
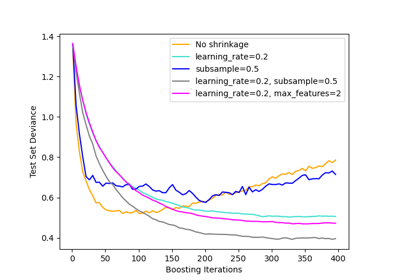
learning_rate. There is a trade-off between learning_rate and n_estimators. Values must be in the range[0.0, inf).For an example of the effects of this parameter and its interaction with
subsample, see Gradient Boosting regularization.- n_estimatorsint, default=100
The number of boosting stages to perform. Gradient boosting is fairly robust to over-fitting so a large number usually results in better performance. Values must be in the range
[1, inf).- subsamplefloat, default=1.0
The fraction of samples to be used for fitting the individual base learners. If smaller than 1.0 this results in Stochastic Gradient Boosting.
subsampleinteracts with the parametern_estimators. Choosingsubsample < 1.0leads to a reduction of variance and an increase in bias. Values must be in the range(0.0, 1.0].- criterion{‘friedman_mse’, ‘squared_error’}, default=’friedman_mse’
The function to measure the quality of a split. Supported criteria are ‘friedman_mse’ for the mean squared error with improvement score by Friedman, ‘squared_error’ for mean squared error. The default value of ‘friedman_mse’ is generally the best as it can provide a better approximation in some cases.
Added in version 0.18.
- min_samples_splitint or float, default=2
The minimum number of samples required to split an internal node:
If int, values must be in the range
[2, inf).If float, values must be in the range
(0.0, 1.0]andmin_samples_splitwill beceil(min_samples_split * n_samples).
Changed in version 0.18: Added float values for fractions.
- min_samples_leafint or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least
min_samples_leaftraining samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.If int, values must be in the range
[1, inf).If float, values must be in the range
(0.0, 1.0)andmin_samples_leafwill beceil(min_samples_leaf * n_samples).
Changed in version 0.18: Added float values for fractions.
- min_weight_fraction_leaffloat, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample_weight is not provided. Values must be in the range
[0.0, 0.5].- max_depthint or None, default=3
Maximum depth of the individual regression estimators. The maximum depth limits the number of nodes in the tree. Tune this parameter for best performance; the best value depends on the interaction of the input variables. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min_samples_split samples. If int, values must be in the range
[1, inf).- min_impurity_decreasefloat, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value. Values must be in the range
[0.0, inf).The weighted impurity decrease equation is the following:
N_t / N * (impurity - N_t_R / N_t * right_impurity - N_t_L / N_t * left_impurity)
where
Nis the total number of samples,N_tis the number of samples at the current node,N_t_Lis the number of samples in the left child, andN_t_Ris the number of samples in the right child.N,N_t,N_t_RandN_t_Lall refer to the weighted sum, ifsample_weightis passed.Added in version 0.19.
- initestimator or ‘zero’, default=None
An estimator object that is used to compute the initial predictions.
inithas to provide fit and predict_proba. If ‘zero’, the initial raw predictions are set to zero. By default, aDummyEstimatorpredicting the classes priors is used.- random_stateint, RandomState instance or None, default=None
Controls the random seed given to each Tree estimator at each boosting iteration. In addition, it controls the random permutation of the features at each split (see Notes for more details). It also controls the random splitting of the training data to obtain a validation set if
n_iter_no_changeis not None. Pass an int for reproducible output across multiple function calls. See Glossary.- max_features{‘sqrt’, ‘log2’}, int or float, default=None
The number of features to consider when looking for the best split:
If int, values must be in the range
[1, inf).If float, values must be in the range
(0.0, 1.0]and the features considered at each split will bemax(1, int(max_features * n_features_in_)).If ‘sqrt’, then
max_features=sqrt(n_features).If ‘log2’, then
max_features=log2(n_features).If None, then
max_features=n_features.
Choosing
max_features < n_featuresleads to a reduction of variance and an increase in bias.Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than
max_featuresfeatures.- verboseint, default=0
Enable verbose output. If 1 then it prints progress and performance once in a while (the more trees the lower the frequency). If greater than 1 then it prints progress and performance for every tree. Values must be in the range
[0, inf).- max_leaf_nodesint, default=None
Grow trees with
max_leaf_nodesin best-first fashion. Best nodes are defined as relative reduction in impurity. Values must be in the range[2, inf). IfNone, then unlimited number of leaf nodes.- warm_startbool, default=False
When set to
True, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just erase the previous solution. See the Glossary.- validation_fractionfloat, default=0.1
The proportion of training data to set aside as validation set for early stopping. Values must be in the range
(0.0, 1.0). Only used ifn_iter_no_changeis set to an integer.Added in version 0.20.
- n_iter_no_changeint, default=None
n_iter_no_changeis used to decide if early stopping will be used to terminate training when validation score is not improving. By default it is set to None to disable early stopping. If set to a number, it will set asidevalidation_fractionsize of the training data as validation and terminate training when validation score is not improving in all of the previousn_iter_no_changenumbers of iterations. The split is stratified. Values must be in the range[1, inf). See Early stopping in Gradient Boosting.Added in version 0.20.
- tolfloat, default=1e-4
Tolerance for the early stopping. When the loss is not improving by at least tol for
n_iter_no_changeiterations (if set to a number), the training stops. Values must be in the range[0.0, inf).Added in version 0.20.
- ccp_alphanon-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than
ccp_alphawill be chosen. By default, no pruning is performed. Values must be in the range[0.0, inf). See Minimal Cost-Complexity Pruning for details. See Post pruning decision trees with cost complexity pruning for an example of such pruning.Added in version 0.22.
- Attributes:
- n_estimators_int
The number of estimators as selected by early stopping (if
n_iter_no_changeis specified). Otherwise it is set ton_estimators.Added in version 0.20.
- n_trees_per_iteration_int
The number of trees that are built at each iteration. For binary classifiers, this is always 1.
Added in version 1.4.0.
feature_importances_ndarray of shape (n_features,)The impurity-based feature importances.
- oob_improvement_ndarray of shape (n_estimators,)
The improvement in loss on the out-of-bag samples relative to the previous iteration.
oob_improvement_[0]is the improvement in loss of the first stage over theinitestimator. Only available ifsubsample < 1.0.- oob_scores_ndarray of shape (n_estimators,)
The full history of the loss values on the out-of-bag samples. Only available if
subsample < 1.0.Added in version 1.3.
- oob_score_float
The last value of the loss on the out-of-bag samples. It is the same as
oob_scores_[-1]. Only available ifsubsample < 1.0.Added in version 1.3.
- train_score_ndarray of shape (n_estimators,)
The i-th score
train_score_[i]is the loss of the model at iterationion the in-bag sample. Ifsubsample == 1this is the loss on the training data.- init_estimator
The estimator that provides the initial predictions. Set via the
initargument.- estimators_ndarray of DecisionTreeRegressor of shape (n_estimators,
n_trees_per_iteration_) The collection of fitted sub-estimators.
n_trees_per_iteration_is 1 for binary classification, otherwisen_classes.- classes_ndarray of shape (n_classes,)
The classes labels.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
- n_classes_int
The number of classes.
- max_features_int
The inferred value of max_features.
See also
HistGradientBoostingClassifierHistogram-based Gradient Boosting Classification Tree.
sklearn.tree.DecisionTreeClassifierA decision tree classifier.
RandomForestClassifierA meta-estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting.
AdaBoostClassifierA meta-estimator that begins by fitting a classifier on the original dataset and then fits additional copies of the classifier on the same dataset where the weights of incorrectly classified instances are adjusted such that subsequent classifiers focus more on difficult cases.
Notes
The features are always randomly permuted at each split. Therefore, the best found split may vary, even with the same training data and
max_features=n_features, if the improvement of the criterion is identical for several splits enumerated during the search of the best split. To obtain a deterministic behaviour during fitting,random_statehas to be fixed.References
J. Friedman, Greedy Function Approximation: A Gradient Boosting Machine, The Annals of Statistics, Vol. 29, No. 5, 2001.
Friedman, Stochastic Gradient Boosting, 1999
T. Hastie, R. Tibshirani and J. Friedman. Elements of Statistical Learning Ed. 2, Springer, 2009.
Examples
The following example shows how to fit a gradient boosting classifier with 100 decision stumps as weak learners.
>>> from sklearn.datasets import make_hastie_10_2 >>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0) >>> X_train, X_test = X[:2000], X[2000:] >>> y_train, y_test = y[:2000], y[2000:]
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0, ... max_depth=1, random_state=0).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.913
- apply(X)[source]#
Apply trees in the ensemble to X, return leaf indices.
Added in version 0.17.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, its dtype will be converted to
dtype=np.float32. If a sparse matrix is provided, it will be converted to a sparsecsr_matrix.
- Returns:
- X_leavesarray-like of shape (n_samples, n_estimators, n_classes)
For each datapoint x in X and for each tree in the ensemble, return the index of the leaf x ends up in each estimator. In the case of binary classification n_classes is 1.
- decision_function(X)[source]#
Compute the decision function of
X.- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.
- Returns:
- scorendarray of shape (n_samples, n_classes) or (n_samples,)
The decision function of the input samples, which corresponds to the raw values predicted from the trees of the ensemble . The order of the classes corresponds to that in the attribute classes_. Regression and binary classification produce an array of shape (n_samples,).
- fit(X, y, sample_weight=None, monitor=None)[source]#
Fit the gradient boosting model.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.- yarray-like of shape (n_samples,)
Target values (strings or integers in classification, real numbers in regression) For classification, labels must correspond to classes.
- sample_weightarray-like of shape (n_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. In the case of classification, splits are also ignored if they would result in any single class carrying a negative weight in either child node.
- monitorcallable, default=None
The monitor is called after each iteration with the current iteration, a reference to the estimator and the local variables of
_fit_stagesas keyword argumentscallable(i, self, locals()). If the callable returnsTruethe fitting procedure is stopped. The monitor can be used for various things such as computing held-out estimates, early stopping, model introspect, and snapshotting.
- Returns:
- selfobject
Fitted estimator.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- predict(X)[source]#
Predict class for X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.
- Returns:
- yndarray of shape (n_samples,)
The predicted values.
- predict_log_proba(X)[source]#
Predict class log-probabilities for X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.
- Returns:
- pndarray of shape (n_samples, n_classes)
The class log-probabilities of the input samples. The order of the classes corresponds to that in the attribute classes_.
- Raises:
- AttributeError
If the
lossdoes not support probabilities.
- predict_proba(X)[source]#
Predict class probabilities for X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.
- Returns:
- pndarray of shape (n_samples, n_classes)
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute classes_.
- Raises:
- AttributeError
If the
lossdoes not support probabilities.
- score(X, y, sample_weight=None)[source]#
Return accuracy on provided data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True labels for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
Mean accuracy of
self.predict(X)w.r.t.y.
- set_fit_request(*, monitor: bool | None | str = '$UNCHANGED$', sample_weight: bool | None | str = '$UNCHANGED$') GradientBoostingClassifier[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- monitorstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
monitorparameter infit.- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') GradientBoostingClassifier[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
- staged_decision_function(X)[source]#
Compute decision function of
Xfor each iteration.This method allows monitoring (i.e. determine error on testing set) after each stage.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.
- Yields:
- scoregenerator of ndarray of shape (n_samples, k)
The decision function of the input samples, which corresponds to the raw values predicted from the trees of the ensemble . The classes corresponds to that in the attribute classes_. Regression and binary classification are special cases with
k == 1, otherwisek==n_classes.
- staged_predict(X)[source]#
Predict class at each stage for X.
This method allows monitoring (i.e. determine error on testing set) after each stage.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.
- Yields:
- ygenerator of ndarray of shape (n_samples,)
The predicted value of the input samples.
- staged_predict_proba(X)[source]#
Predict class probabilities at each stage for X.
This method allows monitoring (i.e. determine error on testing set) after each stage.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The input samples. Internally, it will be converted to
dtype=np.float32and if a sparse matrix is provided to a sparsecsr_matrix.
- Yields:
- ygenerator of ndarray of shape (n_samples,)
The predicted value of the input samples.