`sklearn.linear_model`.BayesianRidge¶

class sklearn.linear_model.BayesianRidge(*, max_iter=None, tol=0.001, alpha_1=1e-06, alpha_2=1e-06, lambda_1=1e-06, lambda_2=1e-06, alpha_init=None, lambda_init=None, compute_score=False, fit_intercept=True, copy_X=True, verbose=False, n_iter='deprecated')[source]¶

Bayesian ridge regression.

Fit a Bayesian ridge model. See the Notes section for details on this implementation and the optimization of the regularization parameters lambda (precision of the weights) and alpha (precision of the noise).

See also

ARDRegression: Bayesian ARD regression.

Notes

There exist several strategies to perform Bayesian ridge regression. This implementation is based on the algorithm described in Appendix A of (Tipping, 2001) where updates of the regularization parameters are done as suggested in (MacKay, 1992). Note that according to A New View of Automatic Relevance Determination (Wipf and Nagarajan, 2008) these update rules do not guarantee that the marginal likelihood is increasing between two consecutive iterations of the optimization.

References

D. J. C. MacKay, Bayesian Interpolation, Computation and Neural Systems, Vol. 4, No. 3, 1992.

M. E. Tipping, Sparse Bayesian Learning and the Relevance Vector Machine, Journal of Machine Learning Research, Vol. 1, 2001.

Examples

>>> from sklearn import linear_model
>>> clf = linear_model.BayesianRidge()
>>> clf.fit([[0,0], [1, 1], [2, 2]], [0, 1, 2])
BayesianRidge()
>>> clf.predict([[1, 1]])
array([1.])

Methods

`fit`(X, y[, sample_weight])	Fit the model.
`get_metadata_routing`()	Get metadata routing of this object.
`get_params`([deep])	Get parameters for this estimator.
`predict`(X[, return_std])	Predict using the linear model.
`score`(X, y[, sample_weight])	Return the coefficient of determination of the prediction.
`set_fit_request`(*[, sample_weight])	Request metadata passed to the `fit` method.
`set_params`(**params)	Set the parameters of this estimator.
`set_predict_request`(*[, return_std])	Request metadata passed to the `predict` method.
`set_score_request`(*[, sample_weight])	Request metadata passed to the `score` method.

fit(X, y, sample_weight=None)[source]¶

Fit the model.

Parameters:

Xndarray of shape (n_samples, n_features): Training data.
yndarray of shape (n_samples,): Target values. Will be cast to X’s dtype if necessary.
sample_weightndarray of shape (n_samples,), default=None: Individual weights for each sample.

New in version 0.20: parameter sample_weight support to BayesianRidge.

Returns:

selfobject: Returns the instance itself.

get_metadata_routing()[source]¶

Get metadata routing of this object.

Please check User Guide on how the routing mechanism works.

Returns:

routingMetadataRequest: A MetadataRequest encapsulating routing information.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

predict(X, return_std=False)[source]¶

Predict using the linear model.

In addition to the mean of the predictive distribution, also its standard deviation can be returned.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): Samples.
return_stdbool, default=False: Whether to return the standard deviation of posterior prediction.

Returns:

y_meanarray-like of shape (n_samples,): Mean of predictive distribution of query points.
y_stdarray-like of shape (n_samples,): Standard deviation of predictive distribution of query points.

score(X, y, sample_weight=None)[source]¶

Return the coefficient of determination of the prediction.

The coefficient of determination $R^2$ is defined as $(1 - \frac{u}{v})$, where $u$ is the residual sum of squares ((y_true - y_pred)** 2).sum() and $v$ is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a $R^2$ score of 0.0.

Parameters:

Xarray-like of shape (n_samples, n_features): Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.
yarray-like of shape (n_samples,) or (n_samples, n_outputs): True values for X.
sample_weightarray-like of shape (n_samples,), default=None: Sample weights.

Returns:

scorefloat: $R^2$ of self.predict(X) w.r.t. y.

Notes

The $R^2$ score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of r2_score. This influences the score method of all the multioutput regressors (except for MultiOutputRegressor).

set_fit_request(*, sample_weight: Union[bool, None, str] = '$UNCHANGED$') → BayesianRidge[source]¶

Request metadata passed to the fit method.

Note that this method is only relevant if enable_metadata_routing=True (see sklearn.set_config). Please see User Guide on how the routing mechanism works.

The options for each parameter are:

True: metadata is requested, and passed to fit if provided. The request is ignored if metadata is not provided.
False: metadata is not requested and the meta-estimator will not pass it to fit.
None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.
str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

New in version 1.3.

Note

This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a Pipeline. Otherwise it has no effect.

Parameters:

sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED: Metadata routing for sample_weight parameter in fit.

Returns:

selfobject: The updated object.

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

set_predict_request(*, return_std: Union[bool, None, str] = '$UNCHANGED$') → BayesianRidge[source]¶

Request metadata passed to the predict method.

Note that this method is only relevant if enable_metadata_routing=True (see sklearn.set_config). Please see User Guide on how the routing mechanism works.

The options for each parameter are:

True: metadata is requested, and passed to predict if provided. The request is ignored if metadata is not provided.
False: metadata is not requested and the meta-estimator will not pass it to predict.
None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.
str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

New in version 1.3.

Note

This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a Pipeline. Otherwise it has no effect.

Parameters:

return_stdstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED: Metadata routing for return_std parameter in predict.

Returns:

selfobject: The updated object.

set_score_request(*, sample_weight: Union[bool, None, str] = '$UNCHANGED$') → BayesianRidge[source]¶

Request metadata passed to the score method.

Note that this method is only relevant if enable_metadata_routing=True (see sklearn.set_config). Please see User Guide on how the routing mechanism works.

The options for each parameter are:

True: metadata is requested, and passed to score if provided. The request is ignored if metadata is not provided.
False: metadata is not requested and the meta-estimator will not pass it to score.
None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.
str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

New in version 1.3.

Note

This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a Pipeline. Otherwise it has no effect.

Parameters:

sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED: Metadata routing for sample_weight parameter in score.

Returns:

selfobject: The updated object.

Examples using `sklearn.linear_model.BayesianRidge`¶

Feature agglomeration vs. univariate selection

Comparing Linear Bayesian Regressors

Curve Fitting with Bayesian Ridge Regression

L1-based models for Sparse Signals

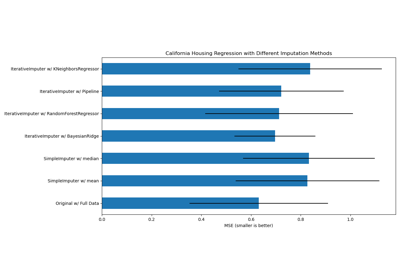
Imputing missing values with variants of IterativeImputer

sklearn.linear_model.BayesianRidge¶

Examples using sklearn.linear_model.BayesianRidge¶

`sklearn.linear_model`.BayesianRidge¶

Examples using `sklearn.linear_model.BayesianRidge`¶