sklearn.decomposition.NMF

class sklearn.decomposition.NMF(n_components=None, *, init=None, solver='cd', beta_loss='frobenius', tol=0.0001, max_iter=200, random_state=None, alpha_W=0.0, alpha_H='same', l1_ratio=0.0, verbose=0, shuffle=False)

Non-Negative Matrix Factorization (NMF).

Find two non-negative matrices, i.e. matrices with all non-negative elements, (W, H) whose product approximates the non-negative matrix X. This factorization can be used for example for dimensionality reduction, source separation or topic extraction.

The objective function is:

\[ \begin{align}\begin{aligned}L(W, H) &= 0.5 * ||X - WH||_{loss}^2\\&+ alpha\_W * l1\_ratio * n\_features * ||vec(W)||_1\\&+ alpha\_H * l1\_ratio * n\_samples * ||vec(H)||_1\\&+ 0.5 * alpha\_W * (1 - l1\_ratio) * n\_features * ||W||_{Fro}^2\\&+ 0.5 * alpha\_H * (1 - l1\_ratio) * n\_samples * ||H||_{Fro}^2\end{aligned}\end{align} \]

Where:

\(||A||_{Fro}^2 = \sum_{i,j} A_{ij}^2\) (Frobenius norm)

\(||vec(A)||_1 = \sum_{i,j} abs(A_{ij})\) (Elementwise L1 norm)

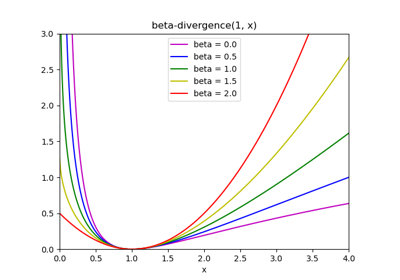
The generic norm \(||X - WH||_{loss}\) may represent the Frobenius norm or another supported beta-divergence loss. The choice between options is controlled by the beta_loss parameter.

The regularization terms are scaled by n_features for W and by n_samples for H to keep their impact balanced with respect to one another and to the data fit term as independent as possible of the size n_samples of the training set.

The objective function is minimized with an alternating minimization of W and H.

Note that the transformed data is named W and the components matrix is named H. In the NMF literature, the naming convention is usually the opposite since the data matrix X is transposed.

Read more in the User Guide.

Parameters:

n_componentsint, default=None

Number of components, if n_components is not set all features are kept.

init{‘random’, ‘nndsvd’, ‘nndsvda’, ‘nndsvdar’, ‘custom’}, default=None

Method used to initialize the procedure. Valid options:

• None: ‘nndsvda’ if n_components <= min(n_samples, n_features), otherwise random.

• 'random': non-negative random matrices, scaled with: sqrt(X.mean() / n_components)

• 'nndsvd': Nonnegative Double Singular Value Decomposition (NNDSVD) initialization (better for sparseness)

• 'nndsvda': NNDSVD with zeros filled with the average of X (better when sparsity is not desired)

• 'nndsvdar' NNDSVD with zeros filled with small random values (generally faster, less accurate alternative to NNDSVDa for when sparsity is not desired)

• 'custom': use custom matrices W and H

Changed in version 1.1: When init=None and n_components is less than n_samples and n_features defaults to nndsvda instead of nndsvd.

solver{‘cd’, ‘mu’}, default=’cd’

Numerical solver to use:

• ‘cd’ is a Coordinate Descent solver.

• ‘mu’ is a Multiplicative Update solver.

New in version 0.17: Coordinate Descent solver.

New in version 0.19: Multiplicative Update solver.

beta_lossfloat or {‘frobenius’, ‘kullback-leibler’, ‘itakura-saito’}, default=’frobenius’

Beta divergence to be minimized, measuring the distance between X and the dot product WH. Note that values different from ‘frobenius’ (or 2) and ‘kullback-leibler’ (or 1) lead to significantly slower fits. Note that for beta_loss <= 0 (or ‘itakura-saito’), the input matrix X cannot contain zeros. Used only in ‘mu’ solver.

New in version 0.19.

tolfloat, default=1e-4

Tolerance of the stopping condition.

max_iterint, default=200

Maximum number of iterations before timing out.

random_stateint, RandomState instance or None, default=None

Used for initialisation (when init == ‘nndsvdar’ or ‘random’), and in Coordinate Descent. Pass an int for reproducible results across multiple function calls. See Glossary.

alpha_Wfloat, default=0.0

Constant that multiplies the regularization terms of W. Set it to zero (default) to have no regularization on W.

New in version 1.0.

alpha_Hfloat or “same”, default=”same”

Constant that multiplies the regularization terms of H. Set it to zero to have no regularization on H. If “same” (default), it takes the same value as alpha_W.

New in version 1.0.

l1_ratiofloat, default=0.0

The regularization mixing parameter, with 0 <= l1_ratio <= 1. For l1_ratio = 0 the penalty is an elementwise L2 penalty (aka Frobenius Norm). For l1_ratio = 1 it is an elementwise L1 penalty. For 0 < l1_ratio < 1, the penalty is a combination of L1 and L2.

New in version 0.17: Regularization parameter l1_ratio used in the Coordinate Descent solver.

verboseint, default=0

Whether to be verbose.

shufflebool, default=False

If true, randomize the order of coordinates in the CD solver.

New in version 0.17: shuffle parameter used in the Coordinate Descent solver.

Attributes:

components_ndarray of shape (n_components, n_features)

Factorization matrix, sometimes called ‘dictionary’.

n_components_int

The number of components. It is same as the n_components parameter if it was given. Otherwise, it will be same as the number of features.

reconstruction_err_float

Frobenius norm of the matrix difference, or beta-divergence, between the training data X and the reconstructed data WH from the fitted model.

n_iter_int

Actual number of iterations.

n_features_in_int

Number of features seen during fit.

New in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

See also

DictionaryLearning

Find a dictionary that sparsely encodes data.

MiniBatchSparsePCA

Mini-batch Sparse Principal Components Analysis.

PCA

Principal component analysis.

SparseCoder

Find a sparse representation of data from a fixed, precomputed dictionary.

SparsePCA

Sparse Principal Components Analysis.

TruncatedSVD

Dimensionality reduction using truncated SVD.

References

[1]

“Fast local algorithms for large scale nonnegative matrix and tensor factorizations” Cichocki, Andrzej, and P. H. A. N. Anh-Huy. IEICE transactions on fundamentals of electronics, communications and computer sciences 92.3: 708-721, 2009.

[2]

“Algorithms for nonnegative matrix factorization with the beta-divergence” Fevotte, C., & Idier, J. (2011). Neural Computation, 23(9).

Examples

>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]])
>>> from sklearn.decomposition import NMF
>>> model = NMF(n_components=2, init='random', random_state=0)
>>> W = model.fit_transform(X)
>>> H = model.components_

Methods

fit(X[, y])	Learn a NMF model for the data X.
fit_transform(X[, y, W, H])	Learn a NMF model for the data X and returns the transformed data.
get_feature_names_out([input_features])	Get output feature names for transformation.
get_params([deep])	Get parameters for this estimator.
inverse_transform(W)	Transform data back to its original space.
set_output(*[, transform])	Set output container.
set_params(**params)	Set the parameters of this estimator.
transform(X)	Transform the data X according to the fitted NMF model.

fit(X, y=None, **params)

Learn a NMF model for the data X.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

Training vector, where n_samples is the number of samples and n_features is the number of features.

yIgnored

Not used, present for API consistency by convention.

**paramskwargs

Parameters (keyword arguments) and values passed to the fit_transform instance.

Returns:

selfobject

Returns the instance itself.

fit_transform(X, y=None, W=None, H=None)

Learn a NMF model for the data X and returns the transformed data.

This is more efficient than calling fit followed by transform.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

Training vector, where n_samples is the number of samples and n_features is the number of features.

yIgnored

Not used, present for API consistency by convention.

Warray-like of shape (n_samples, n_components)

If init=’custom’, it is used as initial guess for the solution.

Harray-like of shape (n_components, n_features)

If init=’custom’, it is used as initial guess for the solution.

Returns:

Wndarray of shape (n_samples, n_components)

Transformed data.

get_feature_names_out(input_features=None)

Get output feature names for transformation.

The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are: ["class_name0", "class_name1", "class_name2"].

Parameters:

input_featuresarray-like of str or None, default=None

Only used to validate feature names with the names seen in fit.

Returns:

feature_names_outndarray of str objects

Transformed feature names.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

inverse_transform(W)

Transform data back to its original space.

New in version 0.18.

Parameters:

W{ndarray, sparse matrix} of shape (n_samples, n_components)

Transformed data matrix.

Returns:

X{ndarray, sparse matrix} of shape (n_samples, n_features)

Returns a data matrix of the original shape.

set_output(*, transform=None)

Set output container.

See Introducing the set_output API for an example on how to use the API.

Parameters:

transform{“default”, “pandas”}, default=None

Configure output of transform and fit_transform.

• "default": Default output format of a transformer

• "pandas": DataFrame output

• None: Transform configuration is unchanged

Returns:

selfestimator instance

Estimator instance.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

transform(X)

Transform the data X according to the fitted NMF model.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

Training vector, where n_samples is the number of samples and n_features is the number of features.

Returns:

Wndarray of shape (n_samples, n_components)

Transformed data.

Examples using sklearn.decomposition.NMF

Beta-divergence loss functions

Beta-divergence loss functions

Faces dataset decompositions

Faces dataset decompositions

Topic extraction with Non-negative Matrix Factorization and Latent Dirichlet Allocation

Topic extraction with Non-negative Matrix Factorization and Latent Dirichlet Allocation

Selecting dimensionality reduction with Pipeline and GridSearchCV

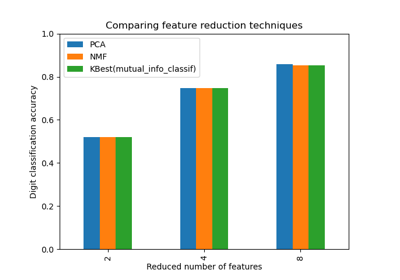
Selecting dimensionality reduction with Pipeline and GridSearchCV