Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder.
FastICA on 2D point clouds#
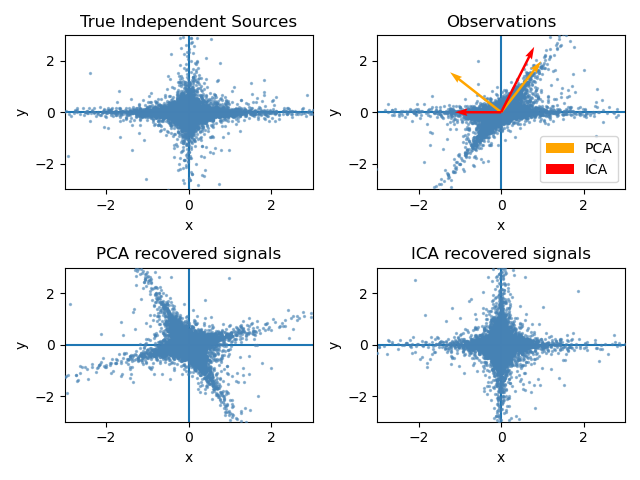
This example illustrates visually in the feature space a comparison by results using two different component analysis techniques.
Independent component analysis (ICA) vs Principal component analysis (PCA).
Representing ICA in the feature space gives the view of ‘geometric ICA’: ICA is an algorithm that finds directions in the feature space corresponding to projections with high non-Gaussianity. These directions need not be orthogonal in the original feature space, but they are orthogonal in the whitened feature space, in which all directions correspond to the same variance.
PCA, on the other hand, finds orthogonal directions in the raw feature space that correspond to directions accounting for maximum variance.
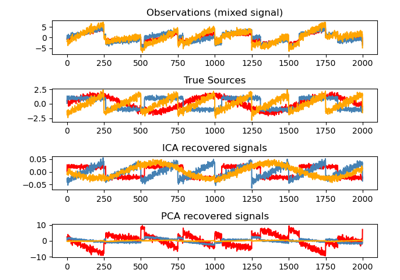
Here we simulate independent sources using a highly non-Gaussian process, 2 student T with a low number of degrees of freedom (top left figure). We mix them to create observations (top right figure). In this raw observation space, directions identified by PCA are represented by orange vectors. We represent the signal in the PCA space, after whitening by the variance corresponding to the PCA vectors (lower left). Running ICA corresponds to finding a rotation in this space to identify the directions of largest non-Gaussianity (lower right).
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Generate sample data#
import numpy as np
from sklearn.decomposition import PCA, FastICA
rng = np.random.RandomState(42)
S = rng.standard_t(1.5, size=(20000, 2))
S[:, 0] *= 2.0
# Mix data
A = np.array([[1, 1], [0, 2]]) # Mixing matrix
X = np.dot(S, A.T) # Generate observations
pca = PCA()
S_pca_ = pca.fit(X).transform(X)
ica = FastICA(random_state=rng, whiten="arbitrary-variance")
S_ica_ = ica.fit(X).transform(X) # Estimate the sources
Plot results#
import matplotlib.pyplot as plt
def plot_samples(S, axis_list=None):
plt.scatter(
S[:, 0], S[:, 1], s=2, marker="o", zorder=10, color="steelblue", alpha=0.5
)
if axis_list is not None:
for axis, color, label in axis_list:
x_axis, y_axis = axis / axis.std()
plt.quiver(
(0, 0),
(0, 0),
x_axis,
y_axis,
zorder=11,
width=0.01,
scale=6,
color=color,
label=label,
)
plt.hlines(0, -5, 5, color="black", linewidth=0.5)
plt.vlines(0, -3, 3, color="black", linewidth=0.5)
plt.xlim(-5, 5)
plt.ylim(-3, 3)
plt.gca().set_aspect("equal")
plt.xlabel("x")
plt.ylabel("y")
plt.figure()
plt.subplot(2, 2, 1)
plot_samples(S / S.std())
plt.title("True Independent Sources")
axis_list = [(pca.components_.T, "orange", "PCA"), (ica.mixing_, "red", "ICA")]
plt.subplot(2, 2, 2)
plot_samples(X / np.std(X), axis_list=axis_list)
legend = plt.legend(loc="upper left")
legend.set_zorder(100)
plt.title("Observations")
plt.subplot(2, 2, 3)
plot_samples(S_pca_ / np.std(S_pca_))
plt.title("PCA recovered signals")
plt.subplot(2, 2, 4)
plot_samples(S_ica_ / np.std(S_ica_))
plt.title("ICA recovered signals")
plt.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.36)
plt.tight_layout()
plt.show()
Total running time of the script: (0 minutes 0.338 seconds)
Related examples
Comparison of LDA and PCA 2D projection of Iris dataset
Single estimator versus bagging: bias-variance decomposition
Principal Component Regression vs Partial Least Squares Regression