PCA#
- class sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', n_oversamples=10, power_iteration_normalizer='auto', random_state=None)[source]#
Principal component analysis (PCA).
Linear dimensionality reduction using Singular Value Decomposition of the data to project it to a lower dimensional space. The input data is centered but not scaled for each feature before applying the SVD.
It uses the LAPACK implementation of the full SVD or a randomized truncated SVD by the method of Halko et al. 2009, depending on the shape of the input data and the number of components to extract.
With sparse inputs, the ARPACK implementation of the truncated SVD can be used (i.e. through
scipy.sparse.linalg.svds). Alternatively, one may considerTruncatedSVDwhere the data are not centered.Notice that this class only supports sparse inputs for some solvers such as “arpack” and “covariance_eigh”. See
TruncatedSVDfor an alternative with sparse data.For a usage example, see Principal Component Analysis (PCA) on Iris Dataset
Read more in the User Guide.
- Parameters:
- n_componentsint, float or ‘mle’, default=None
Number of components to keep. if n_components is not set all components are kept:
n_components == min(n_samples, n_features)
If
n_components == 'mle'andsvd_solver == 'full', Minka’s MLE is used to guess the dimension. Use ofn_components == 'mle'will interpretsvd_solver == 'auto'assvd_solver == 'full'.If
0 < n_components < 1andsvd_solver == 'full', select the number of components such that the amount of variance that needs to be explained is greater than the percentage specified by n_components.If
svd_solver == 'arpack', the number of components must be strictly less than the minimum of n_features and n_samples.Hence, the None case results in:
n_components == min(n_samples, n_features) - 1
- copybool, default=True
If False, data passed to fit are overwritten and running fit(X).transform(X) will not yield the expected results, use fit_transform(X) instead.
- whitenbool, default=False
When True (False by default) the
components_vectors are multiplied by the square root of n_samples and then divided by the singular values to ensure uncorrelated outputs with unit component-wise variances.Whitening will remove some information from the transformed signal (the relative variance scales of the components) but can sometime improve the predictive accuracy of the downstream estimators by making their data respect some hard-wired assumptions.
- svd_solver{‘auto’, ‘full’, ‘covariance_eigh’, ‘arpack’, ‘randomized’}, default=’auto’
- “auto” :
The solver is selected by a default ‘auto’ policy is based on
X.shapeandn_components: if the input data has fewer than 1000 features and more than 10 times as many samples, then the “covariance_eigh” solver is used. Otherwise, if the input data is larger than 500x500 and the number of components to extract is lower than 80% of the smallest dimension of the data, then the more efficient “randomized” method is selected. Otherwise the exact “full” SVD is computed and optionally truncated afterwards.- “full” :
Run exact full SVD calling the standard LAPACK solver via
scipy.linalg.svdand select the components by postprocessing- “covariance_eigh” :
Precompute the covariance matrix (on centered data), run a classical eigenvalue decomposition on the covariance matrix typically using LAPACK and select the components by postprocessing. This solver is very efficient for n_samples >> n_features and small n_features. It is, however, not tractable otherwise for large n_features (large memory footprint required to materialize the covariance matrix). Also note that compared to the “full” solver, this solver effectively doubles the condition number and is therefore less numerical stable (e.g. on input data with a large range of singular values).
- “arpack” :
Run SVD truncated to
n_componentscalling ARPACK solver viascipy.sparse.linalg.svds. It requires strictly0 < n_components < min(X.shape)- “randomized” :
Run randomized SVD by the method of Halko et al.
Added in version 0.18.0.
Changed in version 1.5: Added the ‘covariance_eigh’ solver.
- tolfloat, default=0.0
Tolerance for singular values computed by svd_solver == ‘arpack’. Must be of range [0.0, infinity).
Added in version 0.18.0.
- iterated_powerint or ‘auto’, default=’auto’
Number of iterations for the power method computed by svd_solver == ‘randomized’. Must be of range [0, infinity).
Added in version 0.18.0.
- n_oversamplesint, default=10
This parameter is only relevant when
svd_solver="randomized". It corresponds to the additional number of random vectors to sample the range ofXso as to ensure proper conditioning. Seerandomized_svdfor more details.Added in version 1.1.
- power_iteration_normalizer{‘auto’, ‘QR’, ‘LU’, ‘none’}, default=’auto’
Power iteration normalizer for randomized SVD solver. Not used by ARPACK. See
randomized_svdfor more details.Added in version 1.1.
- random_stateint, RandomState instance or None, default=None
Used when the ‘arpack’ or ‘randomized’ solvers are used. Pass an int for reproducible results across multiple function calls. See Glossary.
Added in version 0.18.0.
- Attributes:
- components_ndarray of shape (n_components, n_features)
Principal axes in feature space, representing the directions of maximum variance in the data. Equivalently, the right singular vectors of the centered input data, parallel to its eigenvectors. The components are sorted by decreasing
explained_variance_.- explained_variance_ndarray of shape (n_components,)
The amount of variance explained by each of the selected components. The variance estimation uses
n_samples - 1degrees of freedom.Equal to n_components largest eigenvalues of the covariance matrix of X.
Added in version 0.18.
- explained_variance_ratio_ndarray of shape (n_components,)
Percentage of variance explained by each of the selected components.
If
n_componentsis not set then all components are stored and the sum of the ratios is equal to 1.0.- singular_values_ndarray of shape (n_components,)
The singular values corresponding to each of the selected components. The singular values are equal to the 2-norms of the
n_componentsvariables in the lower-dimensional space.Added in version 0.19.
- mean_ndarray of shape (n_features,)
Per-feature empirical mean, estimated from the training set.
Equal to
X.mean(axis=0).- n_components_int
The estimated number of components. When n_components is set to ‘mle’ or a number between 0 and 1 (with svd_solver == ‘full’) this number is estimated from input data. Otherwise it equals the parameter n_components, or the lesser value of n_features and n_samples if n_components is None.
- n_samples_int
Number of samples in the training data.
- noise_variance_float
The estimated noise covariance following the Probabilistic PCA model from Tipping and Bishop 1999. See “Pattern Recognition and Machine Learning” by C. Bishop, 12.2.1 p. 574 or http://www.miketipping.com/papers/met-mppca.pdf. It is required to compute the estimated data covariance and score samples.
Equal to the average of (min(n_features, n_samples) - n_components) smallest eigenvalues of the covariance matrix of X.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
KernelPCAKernel Principal Component Analysis.
SparsePCASparse Principal Component Analysis.
TruncatedSVDDimensionality reduction using truncated SVD.
IncrementalPCAIncremental Principal Component Analysis.
References
For n_components == ‘mle’, this class uses the method from: Minka, T. P.. “Automatic choice of dimensionality for PCA”. In NIPS, pp. 598-604
Implements the probabilistic PCA model from: Tipping, M. E., and Bishop, C. M. (1999). “Probabilistic principal component analysis”. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 61(3), 611-622. via the score and score_samples methods.
For svd_solver == ‘arpack’, refer to
scipy.sparse.linalg.svds.For svd_solver == ‘randomized’, see: Halko, N., Martinsson, P. G., and Tropp, J. A. (2011). “Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions”. SIAM review, 53(2), 217-288. and also Martinsson, P. G., Rokhlin, V., and Tygert, M. (2011). “A randomized algorithm for the decomposition of matrices”. Applied and Computational Harmonic Analysis, 30(1), 47-68.
Examples
>>> import numpy as np >>> from sklearn.decomposition import PCA >>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) >>> pca = PCA(n_components=2) >>> pca.fit(X) PCA(n_components=2) >>> print(pca.explained_variance_ratio_) [0.9924 0.0075] >>> print(pca.singular_values_) [6.30061 0.54980]
>>> pca = PCA(n_components=2, svd_solver='full') >>> pca.fit(X) PCA(n_components=2, svd_solver='full') >>> print(pca.explained_variance_ratio_) [0.9924 0.00755] >>> print(pca.singular_values_) [6.30061 0.54980]
>>> pca = PCA(n_components=1, svd_solver='arpack') >>> pca.fit(X) PCA(n_components=1, svd_solver='arpack') >>> print(pca.explained_variance_ratio_) [0.99244] >>> print(pca.singular_values_) [6.30061]
- fit(X, y=None)[source]#
Fit the model with X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training data, where
n_samplesis the number of samples andn_featuresis the number of features.- yIgnored
Ignored.
- Returns:
- selfobject
Returns the instance itself.
- fit_transform(X, y=None)[source]#
Fit the model with X and apply the dimensionality reduction on X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training data, where
n_samplesis the number of samples andn_featuresis the number of features.- yIgnored
Ignored.
- Returns:
- X_newndarray of shape (n_samples, n_components)
Transformed values.
Notes
This method returns a Fortran-ordered array. To convert it to a C-ordered array, use ‘np.ascontiguousarray’.
- get_covariance()[source]#
Compute data covariance with the generative model.
cov = components_.T * S**2 * components_ + sigma2 * eye(n_features)where S**2 contains the explained variances, and sigma2 contains the noise variances.- Returns:
- covarray of shape=(n_features, n_features)
Estimated covariance of data.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are:
["class_name0", "class_name1", "class_name2"].- Parameters:
- input_featuresarray-like of str or None, default=None
Only used to validate feature names with the names seen in
fit.
- Returns:
- feature_names_outndarray of str objects
Transformed feature names.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- get_precision()[source]#
Compute data precision matrix with the generative model.
Equals the inverse of the covariance but computed with the matrix inversion lemma for efficiency.
- Returns:
- precisionarray, shape=(n_features, n_features)
Estimated precision of data.
- inverse_transform(X)[source]#
Transform data back to its original space.
In other words, return an input
X_originalwhose transform would be X.- Parameters:
- Xarray-like of shape (n_samples, n_components)
New data, where
n_samplesis the number of samples andn_componentsis the number of components.
- Returns:
- X_originalarray-like of shape (n_samples, n_features)
Original data, where
n_samplesis the number of samples andn_featuresis the number of features.
Notes
If whitening is enabled, inverse_transform will compute the exact inverse operation, which includes reversing whitening.
- score(X, y=None)[source]#
Return the average log-likelihood of all samples.
See. “Pattern Recognition and Machine Learning” by C. Bishop, 12.2.1 p. 574 or http://www.miketipping.com/papers/met-mppca.pdf
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The data.
- yIgnored
Ignored.
- Returns:
- llfloat
Average log-likelihood of the samples under the current model.
- score_samples(X)[source]#
Return the log-likelihood of each sample.
See. “Pattern Recognition and Machine Learning” by C. Bishop, 12.2.1 p. 574 or http://www.miketipping.com/papers/met-mppca.pdf
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The data.
- Returns:
- llndarray of shape (n_samples,)
Log-likelihood of each sample under the current model.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- transform(X)[source]#
Apply dimensionality reduction to X.
X is projected on the first principal components previously extracted from a training set.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data, where
n_samplesis the number of samples andn_featuresis the number of features.
- Returns:
- X_newarray-like of shape (n_samples, n_components)
Projection of X in the first principal components, where
n_samplesis the number of samples andn_componentsis the number of the components.
Gallery examples#
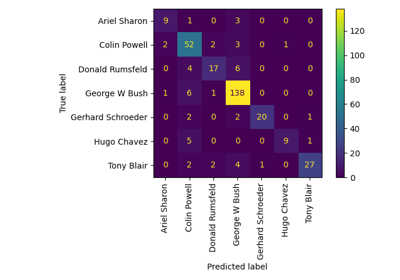
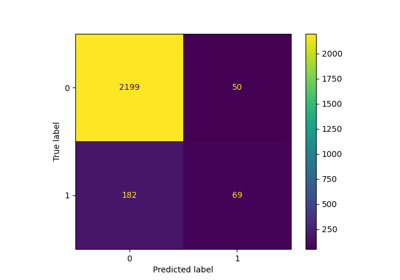
Faces recognition example using eigenfaces and SVMs
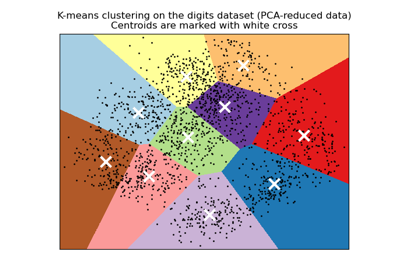
A demo of K-Means clustering on the handwritten digits data

Column Transformer with Heterogeneous Data Sources
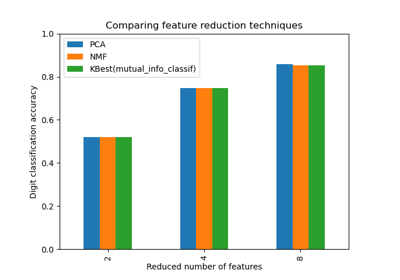
Selecting dimensionality reduction with Pipeline and GridSearchCV
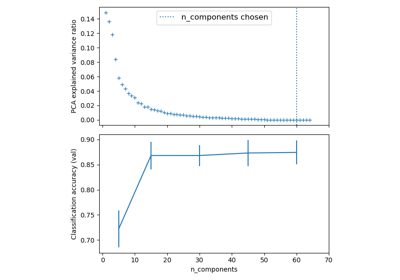
Pipelining: chaining a PCA and a logistic regression
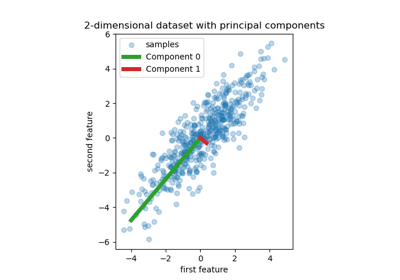
Principal Component Regression vs Partial Least Squares Regression
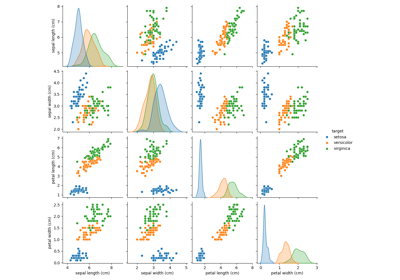
Principal Component Analysis (PCA) on Iris Dataset
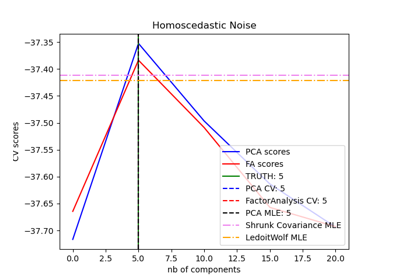
Model selection with Probabilistic PCA and Factor Analysis (FA)
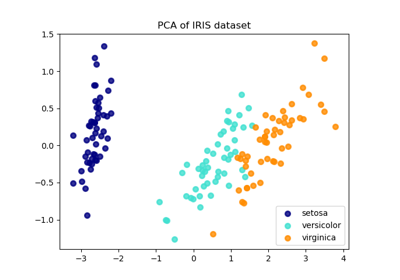
Comparison of LDA and PCA 2D projection of Iris dataset
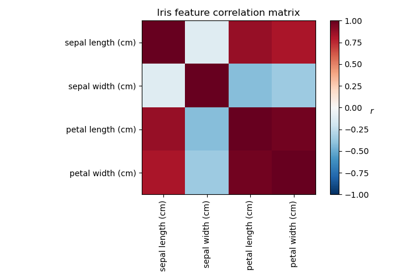
Factor Analysis (with rotation) to visualize patterns
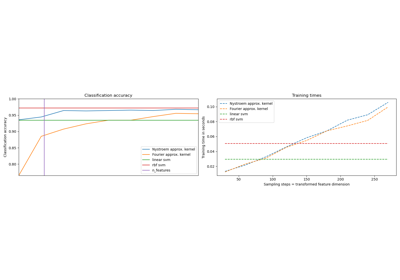
Explicit feature map approximation for RBF kernels
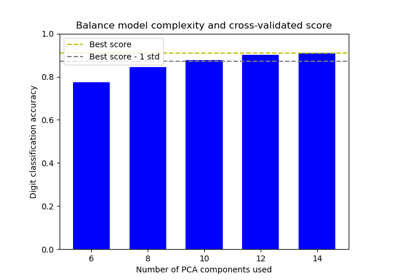
Balance model complexity and cross-validated score
Dimensionality Reduction with Neighborhood Components Analysis