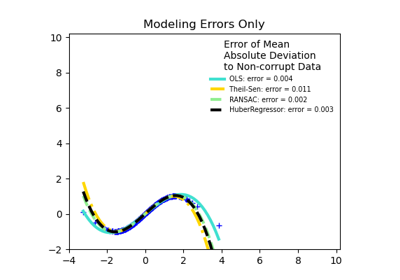
HuberRegressor

class sklearn.linear_model.HuberRegressor(*, epsilon=1.35, max_iter=100, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)

L2-regularized linear regression model that is robust to outliers.

The Huber Regressor optimizes the squared loss for the samples where |(y - Xw - c) / sigma| < epsilon and the absolute loss for the samples where |(y - Xw - c) / sigma| > epsilon, where the model coefficients w, the intercept c and the scale sigma are parameters to be optimized. The parameter sigma makes sure that if y is scaled up or down by a certain factor, one does not need to rescale epsilon to achieve the same robustness. Note that this does not take into account the fact that the different features of X may be of different scales.

The Huber loss function has the advantage of not being heavily influenced by the outliers while not completely ignoring their effect.

Read more in the User Guide

Added in version 0.18.

Parameters:

epsilonfloat, default=1.35

The parameter epsilon controls the number of samples that should be classified as outliers. The smaller the epsilon, the more robust it is to outliers. Epsilon must be in the range [1, inf).

max_iterint, default=100

Maximum number of iterations that scipy.optimize.minimize(method="L-BFGS-B") should run for.

alphafloat, default=0.0001

Strength of the squared L2 regularization. Note that the penalty is equal to alpha * ||w||^2. Must be in the range [0, inf).

warm_startbool, default=False

This is useful if the stored attributes of a previously used model has to be reused. If set to False, then the coefficients will be rewritten for every call to fit. See the Glossary.

fit_interceptbool, default=True

Whether or not to fit the intercept. This can be set to False if the data is already centered around the origin.

tolfloat, default=1e-05

The iteration will stop when max{|proj g_i | i = 1, ..., n} <= tol where pg_i is the i-th component of the projected gradient.

Attributes:

coef_array, shape (n_features,)

Features got by optimizing the L2-regularized Huber loss.

intercept_float

Bias.

scale_float

The value by which |y - Xw - c| is scaled down.

n_features_in_int

Number of features seen during fit.

Added in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

Added in version 1.0.

n_iter_int

Number of iterations that scipy.optimize.minimize(method="L-BFGS-B") has run for.

Changed in version 0.20: In SciPy <= 1.0.0 the number of lbfgs iterations may exceed max_iter. n_iter_ will now report at most max_iter.

outliers_array, shape (n_samples,)

A boolean mask which is set to True where the samples are identified as outliers.

See also

RANSACRegressor

RANSAC (RANdom SAmple Consensus) algorithm.

TheilSenRegressor

Theil-Sen Estimator robust multivariate regression model.

SGDRegressor

Fitted by minimizing a regularized empirical loss with SGD.

References

[1]

Peter J. Huber, Elvezio M. Ronchetti, Robust Statistics Concomitant scale estimates, p. 172

[2]

Art B. Owen (2006), A robust hybrid of lasso and ridge regression.

Examples

>>> import numpy as np
>>> from sklearn.linear_model import HuberRegressor, LinearRegression
>>> from sklearn.datasets import make_regression
>>> rng = np.random.RandomState(0)
>>> X, y, coef = make_regression(
...     n_samples=200, n_features=2, noise=4.0, coef=True, random_state=0)
>>> X[:4] = rng.uniform(10, 20, (4, 2))
>>> y[:4] = rng.uniform(10, 20, 4)
>>> huber = HuberRegressor().fit(X, y)
>>> huber.score(X, y)
-7.284
>>> huber.predict(X[:1,])
array([806.7200])
>>> linear = LinearRegression().fit(X, y)
>>> print("True coefficients:", coef)
True coefficients: [20.4923...  34.1698...]
>>> print("Huber coefficients:", huber.coef_)
Huber coefficients: [17.7906... 31.0106...]
>>> print("Linear Regression coefficients:", linear.coef_)
Linear Regression coefficients: [-1.9221...  7.0226...]

fit(X, y, sample_weight=None)

Fit the model according to the given training data.

Parameters:

Xarray-like, shape (n_samples, n_features)

Training vector, where n_samples is the number of samples and n_features is the number of features.

yarray-like, shape (n_samples,)

Target vector relative to X.

sample_weightarray-like, shape (n_samples,)

Weight given to each sample.

Returns:

selfobject

Fitted HuberRegressor estimator.

get_metadata_routing()

Get metadata routing of this object.

Please check User Guide on how the routing mechanism works.

Returns:

routingMetadataRequest

A MetadataRequest encapsulating routing information.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

predict(X)

Predict using the linear model.

Parameters:

Xarray-like or sparse matrix, shape (n_samples, n_features)

Samples.

Returns:

Carray, shape (n_samples,)

Returns predicted values.

score(X, y, sample_weight=None)

Return coefficient of determination on test data.

The coefficient of determination, \(R^2\), is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares ((y_true - y_pred)** 2).sum() and \(v\) is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a \(R^2\) score of 0.0.

Parameters:

Xarray-like of shape (n_samples, n_features)

Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.

yarray-like of shape (n_samples,) or (n_samples, n_outputs)

True values for X.

sample_weightarray-like of shape (n_samples,), default=None

Sample weights.

Returns:

scorefloat

\(R^2\) of self.predict(X) w.r.t. y.

Notes

The \(R^2\) score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of r2_score. This influences the score method of all the multioutput regressors (except for MultiOutputRegressor).

set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') → HuberRegressor

Configure whether metadata should be requested to be passed to the fit method.

Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with enable_metadata_routing=True (see sklearn.set_config). Please check the User Guide on how the routing mechanism works.

The options for each parameter are:

• True: metadata is requested, and passed to fit if provided. The request is ignored if metadata is not provided.

• False: metadata is not requested and the meta-estimator will not pass it to fit.

• None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.

• str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

Added in version 1.3.

Parameters:

sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED

Metadata routing for sample_weight parameter in fit.

Returns:

selfobject

The updated object.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') → HuberRegressor

Configure whether metadata should be requested to be passed to the score method.

Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with enable_metadata_routing=True (see sklearn.set_config). Please check the User Guide on how the routing mechanism works.

The options for each parameter are:

• True: metadata is requested, and passed to score if provided. The request is ignored if metadata is not provided.

• False: metadata is not requested and the meta-estimator will not pass it to score.

• None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.

• str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

Added in version 1.3.

Parameters:

sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED

Metadata routing for sample_weight parameter in score.

Returns:

selfobject

The updated object.

Gallery examples

HuberRegressor vs Ridge on dataset with strong outliers

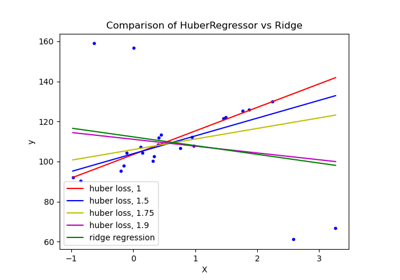
HuberRegressor vs Ridge on dataset with strong outliers

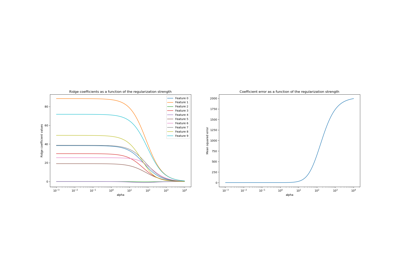
Ridge coefficients as a function of the L2 Regularization

Ridge coefficients as a function of the L2 Regularization

Robust linear estimator fitting

Robust linear estimator fitting