sklearn.metrics.homogeneity_score¶
- sklearn.metrics.homogeneity_score(labels_true, labels_pred)[source]¶
Homogeneity metric of a cluster labeling given a ground truth.
A clustering result satisfies homogeneity if all of its clusters contain only data points which are members of a single class.
This metric is independent of the absolute values of the labels: a permutation of the class or cluster label values won’t change the score value in any way.
This metric is not symmetric: switching
label_truewithlabel_predwill return thecompleteness_scorewhich will be different in general.Read more in the User Guide.
- Parameters:
- labels_truearray-like of shape (n_samples,)
Ground truth class labels to be used as a reference.
- labels_predarray-like of shape (n_samples,)
Cluster labels to evaluate.
- Returns:
- homogeneityfloat
Score between 0.0 and 1.0. 1.0 stands for perfectly homogeneous labeling.
See also
completeness_scoreCompleteness metric of cluster labeling.
v_measure_scoreV-Measure (NMI with arithmetic mean option).
References
Examples
Perfect labelings are homogeneous:
>>> from sklearn.metrics.cluster import homogeneity_score >>> homogeneity_score([0, 0, 1, 1], [1, 1, 0, 0]) 1.0
Non-perfect labelings that further split classes into more clusters can be perfectly homogeneous:
>>> print("%.6f" % homogeneity_score([0, 0, 1, 1], [0, 0, 1, 2])) 1.000000 >>> print("%.6f" % homogeneity_score([0, 0, 1, 1], [0, 1, 2, 3])) 1.000000
Clusters that include samples from different classes do not make for an homogeneous labeling:
>>> print("%.6f" % homogeneity_score([0, 0, 1, 1], [0, 1, 0, 1])) 0.0... >>> print("%.6f" % homogeneity_score([0, 0, 1, 1], [0, 0, 0, 0])) 0.0...
Examples using sklearn.metrics.homogeneity_score¶
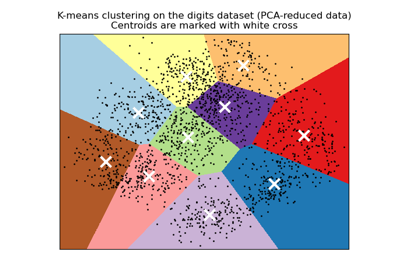
A demo of K-Means clustering on the handwritten digits data