sklearn.covariance.MinCovDet¶
- class sklearn.covariance.MinCovDet(*, store_precision=True, assume_centered=False, support_fraction=None, random_state=None)[source]¶
Minimum Covariance Determinant (MCD): robust estimator of covariance.
The Minimum Covariance Determinant covariance estimator is to be applied on Gaussian-distributed data, but could still be relevant on data drawn from a unimodal, symmetric distribution. It is not meant to be used with multi-modal data (the algorithm used to fit a MinCovDet object is likely to fail in such a case). One should consider projection pursuit methods to deal with multi-modal datasets.
Read more in the User Guide.
- Parameters:
- store_precisionbool, default=True
Specify if the estimated precision is stored.
- assume_centeredbool, default=False
If True, the support of the robust location and the covariance estimates is computed, and a covariance estimate is recomputed from it, without centering the data. Useful to work with data whose mean is significantly equal to zero but is not exactly zero. If False, the robust location and covariance are directly computed with the FastMCD algorithm without additional treatment.
- support_fractionfloat, default=None
The proportion of points to be included in the support of the raw MCD estimate. Default is None, which implies that the minimum value of support_fraction will be used within the algorithm:
(n_samples + n_features + 1) / 2 * n_samples. The parameter must be in the range (0, 1].- random_stateint, RandomState instance or None, default=None
Determines the pseudo random number generator for shuffling the data. Pass an int for reproducible results across multiple function calls. See Glossary.
- Attributes:
- raw_location_ndarray of shape (n_features,)
The raw robust estimated location before correction and re-weighting.
- raw_covariance_ndarray of shape (n_features, n_features)
The raw robust estimated covariance before correction and re-weighting.
- raw_support_ndarray of shape (n_samples,)
A mask of the observations that have been used to compute the raw robust estimates of location and shape, before correction and re-weighting.
- location_ndarray of shape (n_features,)
Estimated robust location.
- covariance_ndarray of shape (n_features, n_features)
Estimated robust covariance matrix.
- precision_ndarray of shape (n_features, n_features)
Estimated pseudo inverse matrix. (stored only if store_precision is True)
- support_ndarray of shape (n_samples,)
A mask of the observations that have been used to compute the robust estimates of location and shape.
- dist_ndarray of shape (n_samples,)
Mahalanobis distances of the training set (on which
fitis called) observations.- n_features_in_int
Number of features seen during fit.
New in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.New in version 1.0.
See also
EllipticEnvelopeAn object for detecting outliers in a Gaussian distributed dataset.
EmpiricalCovarianceMaximum likelihood covariance estimator.
GraphicalLassoSparse inverse covariance estimation with an l1-penalized estimator.
GraphicalLassoCVSparse inverse covariance with cross-validated choice of the l1 penalty.
LedoitWolfLedoitWolf Estimator.
OASOracle Approximating Shrinkage Estimator.
ShrunkCovarianceCovariance estimator with shrinkage.
References
[Rouseeuw1984]P. J. Rousseeuw. Least median of squares regression. J. Am Stat Ass, 79:871, 1984.
[Rousseeuw]A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
[ButlerDavies]R. W. Butler, P. L. Davies and M. Jhun, Asymptotics For The Minimum Covariance Determinant Estimator, The Annals of Statistics, 1993, Vol. 21, No. 3, 1385-1400
Examples
>>> import numpy as np >>> from sklearn.covariance import MinCovDet >>> from sklearn.datasets import make_gaussian_quantiles >>> real_cov = np.array([[.8, .3], ... [.3, .4]]) >>> rng = np.random.RandomState(0) >>> X = rng.multivariate_normal(mean=[0, 0], ... cov=real_cov, ... size=500) >>> cov = MinCovDet(random_state=0).fit(X) >>> cov.covariance_ array([[0.7411..., 0.2535...], [0.2535..., 0.3053...]]) >>> cov.location_ array([0.0813... , 0.0427...])
Methods
correct_covariance(data)Apply a correction to raw Minimum Covariance Determinant estimates.
error_norm(comp_cov[, norm, scaling, squared])Compute the Mean Squared Error between two covariance estimators.
fit(X[, y])Fit a Minimum Covariance Determinant with the FastMCD algorithm.
Get metadata routing of this object.
get_params([deep])Get parameters for this estimator.
Getter for the precision matrix.
mahalanobis(X)Compute the squared Mahalanobis distances of given observations.
reweight_covariance(data)Re-weight raw Minimum Covariance Determinant estimates.
score(X_test[, y])Compute the log-likelihood of
X_testunder the estimated Gaussian model.set_params(**params)Set the parameters of this estimator.
set_score_request(*[, X_test])Request metadata passed to the
scoremethod.- correct_covariance(data)[source]¶
Apply a correction to raw Minimum Covariance Determinant estimates.
Correction using the empirical correction factor suggested by Rousseeuw and Van Driessen in [RVD].
- Parameters:
- dataarray-like of shape (n_samples, n_features)
The data matrix, with p features and n samples. The data set must be the one which was used to compute the raw estimates.
- Returns:
- covariance_correctedndarray of shape (n_features, n_features)
Corrected robust covariance estimate.
References
[RVD]A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
- error_norm(comp_cov, norm='frobenius', scaling=True, squared=True)[source]¶
Compute the Mean Squared Error between two covariance estimators.
- Parameters:
- comp_covarray-like of shape (n_features, n_features)
The covariance to compare with.
- norm{“frobenius”, “spectral”}, default=”frobenius”
The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error
(comp_cov - self.covariance_).- scalingbool, default=True
If True (default), the squared error norm is divided by n_features. If False, the squared error norm is not rescaled.
- squaredbool, default=True
Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.
- Returns:
- resultfloat
The Mean Squared Error (in the sense of the Frobenius norm) between
selfandcomp_covcovariance estimators.
- fit(X, y=None)[source]¶
Fit a Minimum Covariance Determinant with the FastMCD algorithm.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Training data, where
n_samplesis the number of samples andn_featuresis the number of features.- yIgnored
Not used, present for API consistency by convention.
- Returns:
- selfobject
Returns the instance itself.
- get_metadata_routing()[source]¶
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]¶
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- get_precision()[source]¶
Getter for the precision matrix.
- Returns:
- precision_array-like of shape (n_features, n_features)
The precision matrix associated to the current covariance object.
- mahalanobis(X)[source]¶
Compute the squared Mahalanobis distances of given observations.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.
- Returns:
- distndarray of shape (n_samples,)
Squared Mahalanobis distances of the observations.
- reweight_covariance(data)[source]¶
Re-weight raw Minimum Covariance Determinant estimates.
Re-weight observations using Rousseeuw’s method (equivalent to deleting outlying observations from the data set before computing location and covariance estimates) described in [RVDriessen].
- Parameters:
- dataarray-like of shape (n_samples, n_features)
The data matrix, with p features and n samples. The data set must be the one which was used to compute the raw estimates.
- Returns:
- location_reweightedndarray of shape (n_features,)
Re-weighted robust location estimate.
- covariance_reweightedndarray of shape (n_features, n_features)
Re-weighted robust covariance estimate.
- support_reweightedndarray of shape (n_samples,), dtype=bool
A mask of the observations that have been used to compute the re-weighted robust location and covariance estimates.
References
[RVDriessen]A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
- score(X_test, y=None)[source]¶
Compute the log-likelihood of
X_testunder the estimated Gaussian model.The Gaussian model is defined by its mean and covariance matrix which are represented respectively by
self.location_andself.covariance_.- Parameters:
- X_testarray-like of shape (n_samples, n_features)
Test data of which we compute the likelihood, where
n_samplesis the number of samples andn_featuresis the number of features.X_testis assumed to be drawn from the same distribution than the data used in fit (including centering).- yIgnored
Not used, present for API consistency by convention.
- Returns:
- resfloat
The log-likelihood of
X_testwithself.location_andself.covariance_as estimators of the Gaussian model mean and covariance matrix respectively.
- set_params(**params)[source]¶
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_score_request(*, X_test: bool | None | str = '$UNCHANGED$') MinCovDet[source]¶
Request metadata passed to the
scoremethod.Note that this method is only relevant if
enable_metadata_routing=True(seesklearn.set_config). Please see User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.New in version 1.3.
Note
This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a
Pipeline. Otherwise it has no effect.- Parameters:
- X_teststr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
X_testparameter inscore.
- Returns:
- selfobject
The updated object.
Examples using sklearn.covariance.MinCovDet¶
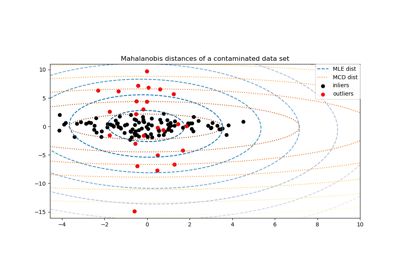
Robust covariance estimation and Mahalanobis distances relevance