MiniBatchKMeans#
- class sklearn.cluster.MiniBatchKMeans(n_clusters=8, *, init='k-means++', max_iter=100, batch_size=1024, verbose=0, compute_labels=True, random_state=None, tol=0.0, max_no_improvement=10, init_size=None, n_init='auto', reassignment_ratio=0.01)[source]#
Mini-Batch K-Means clustering.
Read more in the User Guide.
- Parameters:
- n_clustersint, default=8
The number of clusters to form as well as the number of centroids to generate.
- init{‘k-means++’, ‘random’}, callable or array-like of shape (n_clusters, n_features), default=’k-means++’
Method for initialization:
‘k-means++’ : selects initial cluster centroids using sampling based on an empirical probability distribution of the points’ contribution to the overall inertia. This technique speeds up convergence. The algorithm implemented is “greedy k-means++”. It differs from the vanilla k-means++ by making several trials at each sampling step and choosing the best centroid among them.
‘random’: choose
n_clustersobservations (rows) at random from data for the initial centroids.If an array is passed, it should be of shape (n_clusters, n_features) and gives the initial centers.
If a callable is passed, it should take arguments X, n_clusters and a random state and return an initialization.
For an evaluation of the impact of initialization, see the example Empirical evaluation of the impact of k-means initialization.
- max_iterint, default=100
Maximum number of iterations over the complete dataset before stopping independently of any early stopping criterion heuristics.
- batch_sizeint, default=1024
Size of the mini batches. For faster computations, you can set
batch_size > 256 * number_of_coresto enable parallelism on all cores.Changed in version 1.0:
batch_sizedefault changed from 100 to 1024.- verboseint, default=0
Verbosity mode.
- compute_labelsbool, default=True
Compute label assignment and inertia for the complete dataset once the minibatch optimization has converged in fit.
- random_stateint, RandomState instance or None, default=None
Determines random number generation for centroid initialization and random reassignment. Use an int to make the randomness deterministic. See Glossary.
- tolfloat, default=0.0
Control early stopping based on the relative center changes as measured by a smoothed, variance-normalized of the mean center squared position changes. This early stopping heuristics is closer to the one used for the batch variant of the algorithms but induces a slight computational and memory overhead over the inertia heuristic.
To disable convergence detection based on normalized center change, set tol to 0.0 (default).
- max_no_improvementint, default=10
Control early stopping based on the consecutive number of mini batches that does not yield an improvement on the smoothed inertia.
To disable convergence detection based on inertia, set max_no_improvement to None.
- init_sizeint, default=None
Number of samples to randomly sample for speeding up the initialization (sometimes at the expense of accuracy): the only algorithm is initialized by running a batch KMeans on a random subset of the data. This needs to be larger than n_clusters.
If
None, the heuristic isinit_size = 3 * batch_sizeif3 * batch_size < n_clusters, elseinit_size = 3 * n_clusters.- n_init‘auto’ or int, default=”auto”
Number of random initializations that are tried. In contrast to KMeans, the algorithm is only run once, using the best of the
n_initinitializations as measured by inertia. Several runs are recommended for sparse high-dimensional problems (see Clustering sparse data with k-means).When
n_init='auto', the number of runs depends on the value of init: 3 if usinginit='random'orinitis a callable; 1 if usinginit='k-means++'orinitis an array-like.Added in version 1.2: Added ‘auto’ option for
n_init.Changed in version 1.4: Default value for
n_initchanged to'auto'in version.- reassignment_ratiofloat, default=0.01
Control the fraction of the maximum number of counts for a center to be reassigned. A higher value means that low count centers are more easily reassigned, which means that the model will take longer to converge, but should converge in a better clustering. However, too high a value may cause convergence issues, especially with a small batch size.
- Attributes:
- cluster_centers_ndarray of shape (n_clusters, n_features)
Coordinates of cluster centers.
- labels_ndarray of shape (n_samples,)
Labels of each point (if compute_labels is set to True).
- inertia_float
The value of the inertia criterion associated with the chosen partition if compute_labels is set to True. If compute_labels is set to False, it’s an approximation of the inertia based on an exponentially weighted average of the batch inertiae. The inertia is defined as the sum of square distances of samples to their cluster center, weighted by the sample weights if provided.
- n_iter_int
Number of iterations over the full dataset.
- n_steps_int
Number of minibatches processed.
Added in version 1.0.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
KMeansThe classic implementation of the clustering method based on the Lloyd’s algorithm. It consumes the whole set of input data at each iteration.
Notes
See https://www.eecs.tufts.edu/~dsculley/papers/fastkmeans.pdf
When there are too few points in the dataset, some centers may be duplicated, which means that a proper clustering in terms of the number of requesting clusters and the number of returned clusters will not always match. One solution is to set
reassignment_ratio=0, which prevents reassignments of clusters that are too small.See Compare BIRCH and MiniBatchKMeans for a comparison with
BIRCH.Examples
>>> from sklearn.cluster import MiniBatchKMeans >>> import numpy as np >>> X = np.array([[1, 2], [1, 4], [1, 0], ... [4, 2], [4, 0], [4, 4], ... [4, 5], [0, 1], [2, 2], ... [3, 2], [5, 5], [1, -1]]) >>> # manually fit on batches >>> kmeans = MiniBatchKMeans(n_clusters=2, ... random_state=0, ... batch_size=6, ... n_init="auto") >>> kmeans = kmeans.partial_fit(X[0:6,:]) >>> kmeans = kmeans.partial_fit(X[6:12,:]) >>> kmeans.cluster_centers_ array([[3.375, 3. ], [0.75 , 0.5 ]]) >>> kmeans.predict([[0, 0], [4, 4]]) array([1, 0], dtype=int32) >>> # fit on the whole data >>> kmeans = MiniBatchKMeans(n_clusters=2, ... random_state=0, ... batch_size=6, ... max_iter=10, ... n_init="auto").fit(X) >>> kmeans.cluster_centers_ array([[3.55102041, 2.48979592], [1.06896552, 1. ]]) >>> kmeans.predict([[0, 0], [4, 4]]) array([1, 0], dtype=int32)
For a comparison of Mini-Batch K-Means clustering with other clustering algorithms, see Comparing different clustering algorithms on toy datasets
- fit(X, y=None, sample_weight=None)[source]#
Compute the centroids on X by chunking it into mini-batches.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training instances to cluster. It must be noted that the data will be converted to C ordering, which will cause a memory copy if the given data is not C-contiguous. If a sparse matrix is passed, a copy will be made if it’s not in CSR format.
- yIgnored
Not used, present here for API consistency by convention.
- sample_weightarray-like of shape (n_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
sample_weightis not used during initialization ifinitis a callable or a user provided array.Added in version 0.20.
- Returns:
- selfobject
Fitted estimator.
- fit_predict(X, y=None, sample_weight=None)[source]#
Compute cluster centers and predict cluster index for each sample.
Convenience method; equivalent to calling fit(X) followed by predict(X).
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data to transform.
- yIgnored
Not used, present here for API consistency by convention.
- sample_weightarray-like of shape (n_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
- Returns:
- labelsndarray of shape (n_samples,)
Index of the cluster each sample belongs to.
- fit_transform(X, y=None, sample_weight=None)[source]#
Compute clustering and transform X to cluster-distance space.
Equivalent to fit(X).transform(X), but more efficiently implemented.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data to transform.
- yIgnored
Not used, present here for API consistency by convention.
- sample_weightarray-like of shape (n_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
- Returns:
- X_newndarray of shape (n_samples, n_clusters)
X transformed in the new space.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are:
["class_name0", "class_name1", "class_name2"].- Parameters:
- input_featuresarray-like of str or None, default=None
Only used to validate feature names with the names seen in
fit.
- Returns:
- feature_names_outndarray of str objects
Transformed feature names.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- partial_fit(X, y=None, sample_weight=None)[source]#
Update k means estimate on a single mini-batch X.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training instances to cluster. It must be noted that the data will be converted to C ordering, which will cause a memory copy if the given data is not C-contiguous. If a sparse matrix is passed, a copy will be made if it’s not in CSR format.
- yIgnored
Not used, present here for API consistency by convention.
- sample_weightarray-like of shape (n_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
sample_weightis not used during initialization ifinitis a callable or a user provided array.
- Returns:
- selfobject
Return updated estimator.
- predict(X)[source]#
Predict the closest cluster each sample in X belongs to.
In the vector quantization literature,
cluster_centers_is called the code book and each value returned bypredictis the index of the closest code in the code book.- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data to predict.
- Returns:
- labelsndarray of shape (n_samples,)
Index of the cluster each sample belongs to.
- score(X, y=None, sample_weight=None)[source]#
Opposite of the value of X on the K-means objective.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data.
- yIgnored
Not used, present here for API consistency by convention.
- sample_weightarray-like of shape (n_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
- Returns:
- scorefloat
Opposite of the value of X on the K-means objective.
- set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') MiniBatchKMeans[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_partial_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') MiniBatchKMeans[source]#
Configure whether metadata should be requested to be passed to the
partial_fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed topartial_fitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it topartial_fit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inpartial_fit.
- Returns:
- selfobject
The updated object.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') MiniBatchKMeans[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
- transform(X)[source]#
Transform X to a cluster-distance space.
In the new space, each dimension is the distance to the cluster centers. Note that even if X is sparse, the array returned by
transformwill typically be dense.- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data to transform.
- Returns:
- X_newndarray of shape (n_samples, n_clusters)
X transformed in the new space.
Gallery examples#

Biclustering documents with the Spectral Co-clustering algorithm
Comparing different clustering algorithms on toy datasets
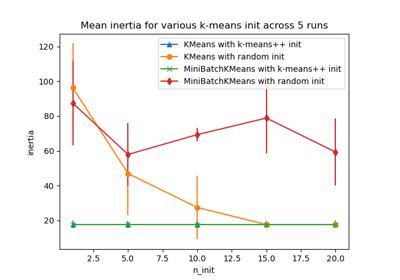
Empirical evaluation of the impact of k-means initialization
Comparison of the K-Means and MiniBatchKMeans clustering algorithms