KMeans#
- class sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init='auto', max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm='lloyd')[source]#
K-Means clustering.
Read more in the User Guide.
- Parameters:
- n_clustersint, default=8
The number of clusters to form as well as the number of centroids to generate.
For an example of how to choose an optimal value for
n_clustersrefer to Selecting the number of clusters with silhouette analysis on KMeans clustering.- init{‘k-means++’, ‘random’}, callable or array-like of shape (n_clusters, n_features), default=’k-means++’
Method for initialization:
‘k-means++’ : selects initial cluster centroids using sampling based on an empirical probability distribution of the points’ contribution to the overall inertia. This technique speeds up convergence. The algorithm implemented is “greedy k-means++”. It differs from the vanilla k-means++ by making several trials at each sampling step and choosing the best centroid among them.
‘random’: choose
n_clustersobservations (rows) at random from data for the initial centroids.If an array is passed, it should be of shape (n_clusters, n_features) and gives the initial centers.
If a callable is passed, it should take arguments X, n_clusters and a random state and return an initialization.
For an example of how to use the different
initstrategies, see A demo of K-Means clustering on the handwritten digits data.For an evaluation of the impact of initialization, see the example Empirical evaluation of the impact of k-means initialization.
- n_init‘auto’ or int, default=’auto’
Number of times the k-means algorithm is run with different centroid seeds. The final results is the best output of
n_initconsecutive runs in terms of inertia. Several runs are recommended for sparse high-dimensional problems (see Clustering sparse data with k-means).When
n_init='auto', the number of runs depends on the value of init: 10 if usinginit='random'orinitis a callable; 1 if usinginit='k-means++'orinitis an array-like.Added in version 1.2: Added ‘auto’ option for
n_init.Changed in version 1.4: Default value for
n_initchanged to'auto'.- max_iterint, default=300
Maximum number of iterations of the k-means algorithm for a single run.
- tolfloat, default=1e-4
Relative tolerance with regards to Frobenius norm of the difference in the cluster centers of two consecutive iterations to declare convergence.
- verboseint, default=0
Verbosity mode.
- random_stateint, RandomState instance or None, default=None
Determines random number generation for centroid initialization. Use an int to make the randomness deterministic. See Glossary.
- copy_xbool, default=True
When pre-computing distances it is more numerically accurate to center the data first. If copy_x is True (default), then the original data is not modified. If False, the original data is modified, and put back before the function returns, but small numerical differences may be introduced by subtracting and then adding the data mean. Note that if the original data is not C-contiguous, a copy will be made even if copy_x is False. If the original data is sparse, but not in CSR format, a copy will be made even if copy_x is False.
- algorithm{“lloyd”, “elkan”}, default=”lloyd”
K-means algorithm to use. The classical EM-style algorithm is
"lloyd". The"elkan"variation can be more efficient on some datasets with well-defined clusters, by using the triangle inequality. However it’s more memory intensive due to the allocation of an extra array of shape(n_samples, n_clusters).Changed in version 0.18: Added Elkan algorithm
Changed in version 1.1: Renamed “full” to “lloyd”, and deprecated “auto” and “full”. Changed “auto” to use “lloyd” instead of “elkan”.
- Attributes:
- cluster_centers_ndarray of shape (n_clusters, n_features)
Coordinates of cluster centers. If the algorithm stops before fully converging (see
tolandmax_iter), these will not be consistent withlabels_.- labels_ndarray of shape (n_samples,)
Labels of each point
- inertia_float
Sum of squared distances of samples to their closest cluster center, weighted by the sample weights if provided.
- n_iter_int
Number of iterations run.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
See also
MiniBatchKMeansAlternative online implementation that does incremental updates of the centers positions using mini-batches. For large scale learning (say n_samples > 10k) MiniBatchKMeans is probably much faster than the default batch implementation.
Notes
The k-means problem is solved using either Lloyd’s or Elkan’s algorithm.
The average complexity is given by O(k n T), where n is the number of samples and T is the number of iteration.
The worst case complexity is given by O(n^(k+2/p)) with n = n_samples, p = n_features. Refer to “How slow is the k-means method?” D. Arthur and S. Vassilvitskii - SoCG2006. for more details.
In practice, the k-means algorithm is very fast (one of the fastest clustering algorithms available), but it falls in local minima. That’s why it can be useful to restart it several times.
If the algorithm stops before fully converging (because of
tolormax_iter),labels_andcluster_centers_will not be consistent, i.e. thecluster_centers_will not be the means of the points in each cluster. Also, the estimator will reassignlabels_after the last iteration to makelabels_consistent withpredicton the training set.Examples
>>> from sklearn.cluster import KMeans >>> import numpy as np >>> X = np.array([[1, 2], [1, 4], [1, 0], ... [10, 2], [10, 4], [10, 0]]) >>> kmeans = KMeans(n_clusters=2, random_state=0, n_init="auto").fit(X) >>> kmeans.labels_ array([1, 1, 1, 0, 0, 0], dtype=int32) >>> kmeans.predict([[0, 0], [12, 3]]) array([1, 0], dtype=int32) >>> kmeans.cluster_centers_ array([[10., 2.], [ 1., 2.]])
For examples of common problems with K-Means and how to address them see Demonstration of k-means assumptions.
For a demonstration of how K-Means can be used to cluster text documents see Clustering text documents using k-means.
For a comparison between K-Means and MiniBatchKMeans refer to example Comparison of the K-Means and MiniBatchKMeans clustering algorithms.
For a comparison between K-Means and BisectingKMeans refer to example Bisecting K-Means and Regular K-Means Performance Comparison.
- fit(X, y=None, sample_weight=None)[source]#
Compute k-means clustering.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
Training instances to cluster. It must be noted that the data will be converted to C ordering, which will cause a memory copy if the given data is not C-contiguous. If a sparse matrix is passed, a copy will be made if it’s not in CSR format.
- yIgnored
Not used, present here for API consistency by convention.
- sample_weightarray-like of shape (n_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
sample_weightis not used during initialization ifinitis a callable or a user provided array.Added in version 0.20.
- Returns:
- selfobject
Fitted estimator.
- fit_predict(X, y=None, sample_weight=None)[source]#
Compute cluster centers and predict cluster index for each sample.
Convenience method; equivalent to calling fit(X) followed by predict(X).
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data to transform.
- yIgnored
Not used, present here for API consistency by convention.
- sample_weightarray-like of shape (n_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
- Returns:
- labelsndarray of shape (n_samples,)
Index of the cluster each sample belongs to.
- fit_transform(X, y=None, sample_weight=None)[source]#
Compute clustering and transform X to cluster-distance space.
Equivalent to fit(X).transform(X), but more efficiently implemented.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data to transform.
- yIgnored
Not used, present here for API consistency by convention.
- sample_weightarray-like of shape (n_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
- Returns:
- X_newndarray of shape (n_samples, n_clusters)
X transformed in the new space.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are:
["class_name0", "class_name1", "class_name2"].- Parameters:
- input_featuresarray-like of str or None, default=None
Only used to validate feature names with the names seen in
fit.
- Returns:
- feature_names_outndarray of str objects
Transformed feature names.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- predict(X)[source]#
Predict the closest cluster each sample in X belongs to.
In the vector quantization literature,
cluster_centers_is called the code book and each value returned bypredictis the index of the closest code in the code book.- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data to predict.
- Returns:
- labelsndarray of shape (n_samples,)
Index of the cluster each sample belongs to.
- score(X, y=None, sample_weight=None)[source]#
Opposite of the value of X on the K-means objective.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data.
- yIgnored
Not used, present here for API consistency by convention.
- sample_weightarray-like of shape (n_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
- Returns:
- scorefloat
Opposite of the value of X on the K-means objective.
- set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') KMeans[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') KMeans[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
- transform(X)[source]#
Transform X to a cluster-distance space.
In the new space, each dimension is the distance to the cluster centers. Note that even if X is sparse, the array returned by
transformwill typically be dense.- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
New data to transform.
- Returns:
- X_newndarray of shape (n_samples, n_clusters)
X transformed in the new space.
Gallery examples#
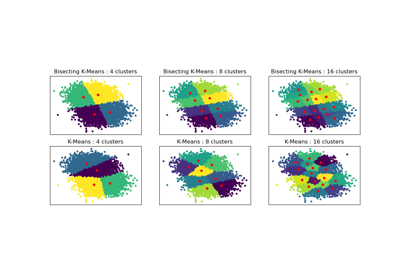
Bisecting K-Means and Regular K-Means Performance Comparison
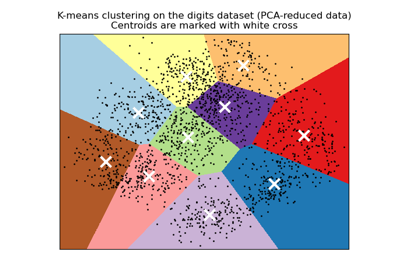
A demo of K-Means clustering on the handwritten digits data
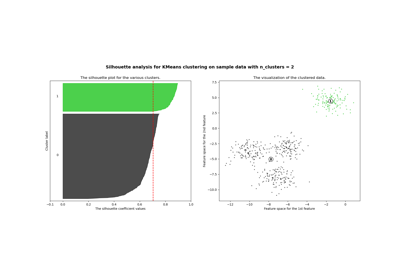
Selecting the number of clusters with silhouette analysis on KMeans clustering
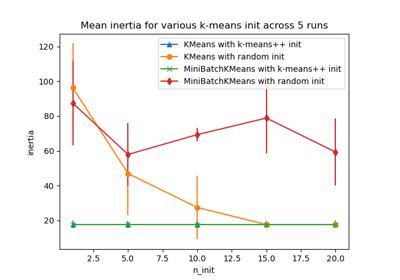
Empirical evaluation of the impact of k-means initialization
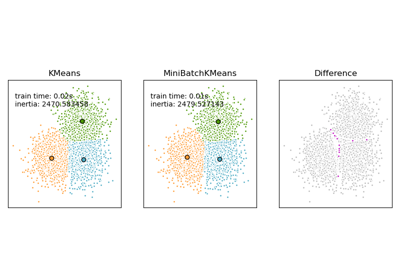
Comparison of the K-Means and MiniBatchKMeans clustering algorithms