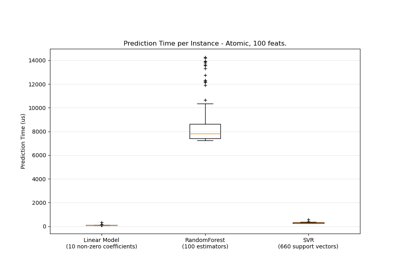
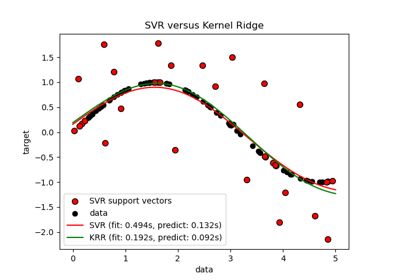
SVR#
- class sklearn.svm.SVR(*, kernel='rbf', degree=3, gamma='scale', coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)[source]#
Epsilon-Support Vector Regression.
The free parameters in the model are C and epsilon.
The implementation is based on libsvm. The fit time complexity is more than quadratic with the number of samples which makes it hard to scale to datasets with more than a couple of 10000 samples. For large datasets consider using
LinearSVRorSGDRegressorinstead, possibly after aNystroemtransformer or other Kernel Approximation.Read more in the User Guide.
- Parameters:
- kernel{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} or callable, default=’rbf’
Specifies the kernel type to be used in the algorithm. If none is given, ‘rbf’ will be used. If a callable is given it is used to precompute the kernel matrix. For an intuitive visualization of different kernel types see Support Vector Regression (SVR) using linear and non-linear kernels
- degreeint, default=3
Degree of the polynomial kernel function (‘poly’). Must be non-negative. Ignored by all other kernels.
- gamma{‘scale’, ‘auto’} or float, default=’scale’
Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
if
gamma='scale'(default) is passed then it uses 1 / (n_features * X.var()) as value of gamma,if ‘auto’, uses 1 / n_features
if float, must be non-negative.
Changed in version 0.22: The default value of
gammachanged from ‘auto’ to ‘scale’.- coef0float, default=0.0
Independent term in kernel function. It is only significant in ‘poly’ and ‘sigmoid’.
- tolfloat, default=1e-3
Tolerance for stopping criterion.
- Cfloat, default=1.0
Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive. The penalty is a squared l2. For an intuitive visualization of the effects of scaling the regularization parameter C, see Scaling the regularization parameter for SVCs.
- epsilonfloat, default=0.1
Epsilon in the epsilon-SVR model. It specifies the epsilon-tube within which no penalty is associated in the training loss function with points predicted within a distance epsilon from the actual value. Must be non-negative.
- shrinkingbool, default=True
Whether to use the shrinking heuristic. See the User Guide.
- cache_sizefloat, default=200
Specify the size of the kernel cache (in MB).
- verbosebool, default=False
Enable verbose output. Note that this setting takes advantage of a per-process runtime setting in libsvm that, if enabled, may not work properly in a multithreaded context.
- max_iterint, default=-1
Hard limit on iterations within solver, or -1 for no limit.
- Attributes:
coef_ndarray of shape (1, n_features)Weights assigned to the features when
kernel="linear".- dual_coef_ndarray of shape (1, n_SV)
Coefficients of the support vector in the decision function.
- fit_status_int
0 if correctly fitted, 1 otherwise (will raise warning)
- intercept_ndarray of shape (1,)
Constants in decision function.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
- n_iter_int
Number of iterations run by the optimization routine to fit the model.
Added in version 1.1.
n_support_ndarray of shape (1,), dtype=int32Number of support vectors for each class.
- shape_fit_tuple of int of shape (n_dimensions_of_X,)
Array dimensions of training vector
X.- support_ndarray of shape (n_SV,)
Indices of support vectors.
- support_vectors_ndarray of shape (n_SV, n_features)
Support vectors.
See also
References
Examples
>>> from sklearn.svm import SVR >>> from sklearn.pipeline import make_pipeline >>> from sklearn.preprocessing import StandardScaler >>> import numpy as np >>> n_samples, n_features = 10, 5 >>> rng = np.random.RandomState(0) >>> y = rng.randn(n_samples) >>> X = rng.randn(n_samples, n_features) >>> regr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2)) >>> regr.fit(X, y) Pipeline(steps=[('standardscaler', StandardScaler()), ('svr', SVR(epsilon=0.2))])
- fit(X, y, sample_weight=None)[source]#
Fit the SVM model according to the given training data.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features) or (n_samples, n_samples)
Training vectors, where
n_samplesis the number of samples andn_featuresis the number of features. For kernel=”precomputed”, the expected shape of X is (n_samples, n_samples).- yarray-like of shape (n_samples,)
Target values (class labels in classification, real numbers in regression).
- sample_weightarray-like of shape (n_samples,), default=None
Per-sample weights. Rescale C per sample. Higher weights force the classifier to put more emphasis on these points.
- Returns:
- selfobject
Fitted estimator.
Notes
If X and y are not C-ordered and contiguous arrays of np.float64 and X is not a scipy.sparse.csr_matrix, X and/or y may be copied.
If X is a dense array, then the other methods will not support sparse matrices as input.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- predict(X)[source]#
Perform regression on samples in X.
For an one-class model, +1 (inlier) or -1 (outlier) is returned.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
For kernel=”precomputed”, the expected shape of X is (n_samples_test, n_samples_train).
- Returns:
- y_predndarray of shape (n_samples,)
The predicted values.
- score(X, y, sample_weight=None)[source]#
Return coefficient of determination on test data.
The coefficient of determination, \(R^2\), is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares
((y_true - y_pred)** 2).sum()and \(v\) is the total sum of squares((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value ofy, disregarding the input features, would get a \(R^2\) score of 0.0.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape
(n_samples, n_samples_fitted), wheren_samples_fittedis the number of samples used in the fitting for the estimator.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True values for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
\(R^2\) of
self.predict(X)w.r.t.y.
Notes
The \(R^2\) score used when calling
scoreon a regressor usesmultioutput='uniform_average'from version 0.23 to keep consistent with default value ofr2_score. This influences thescoremethod of all the multioutput regressors (except forMultiOutputRegressor).
- set_fit_request(*, sample_weight: bool | None | str = '$UNCHANGED$') SVR[source]#
Configure whether metadata should be requested to be passed to the
fitmethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter infit.
- Returns:
- selfobject
The updated object.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') SVR[source]#
Configure whether metadata should be requested to be passed to the
scoremethod.Note that this method is only relevant when this estimator is used as a sub-estimator within a meta-estimator and metadata routing is enabled with
enable_metadata_routing=True(seesklearn.set_config). Please check the User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
- Parameters:
- sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
sample_weightparameter inscore.
- Returns:
- selfobject
The updated object.
Gallery examples#
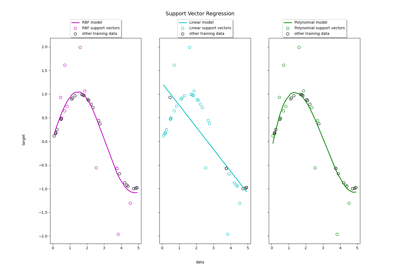
Support Vector Regression (SVR) using linear and non-linear kernels