1.1. Linear Models#

The following are a set of methods intended for regression in which the target value is expected to be a linear combination of the features. In mathematical notation, if \(\hat{y}\) is the predicted value.

\[\hat{y}(w, x) = w_0 + w_1 x_1 + ... + w_p x_p\]

Across the module, we designate the vector \(w = (w_1, ..., w_p)\) as coef_ and \(w_0\) as intercept_.

To perform classification with generalized linear models, see Logistic regression.

1.1.1. Ordinary Least Squares#

LinearRegression fits a linear model with coefficients \(w = (w_1, ..., w_p)\) to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation. Mathematically it solves a problem of the form:

\[\min_{w} || X w - y||_2^2\]

LinearRegression will take in its fit method arrays X, y and will store the coefficients \(w\) of the linear model in its coef_ member:

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression()
>>> reg.coef_
array([0.5, 0.5])

The coefficient estimates for Ordinary Least Squares rely on the independence of the features. When features are correlated and the columns of the design matrix \(X\) have an approximately linear dependence, the design matrix becomes close to singular and as a result, the least-squares estimate becomes highly sensitive to random errors in the observed target, producing a large variance. This situation of multicollinearity can arise, for example, when data are collected without an experimental design.

Examples

Ordinary Least Squares Example

1.1.1.1. Non-Negative Least Squares#

It is possible to constrain all the coefficients to be non-negative, which may be useful when they represent some physical or naturally non-negative quantities (e.g., frequency counts or prices of goods). LinearRegression accepts a boolean positive parameter: when set to True Non-Negative Least Squares are then applied.

Examples

Non-negative least squares

1.1.1.2. Ordinary Least Squares Complexity#

The least squares solution is computed using the singular value decomposition of X. If X is a matrix of shape (n_samples, n_features) this method has a cost of \(O(n_{\text{samples}} n_{\text{features}}^2)\), assuming that \(n_{\text{samples}} \geq n_{\text{features}}\).

1.1.2. Ridge regression and classification#

1.1.2.1. Regression#

Ridge regression addresses some of the problems of Ordinary Least Squares by imposing a penalty on the size of the coefficients. The ridge coefficients minimize a penalized residual sum of squares:

\[\min_{w} || X w - y||_2^2 + \alpha ||w||_2^2\]

The complexity parameter \(\alpha \geq 0\) controls the amount of shrinkage: the larger the value of \(\alpha\), the greater the amount of shrinkage and thus the coefficients become more robust to collinearity.

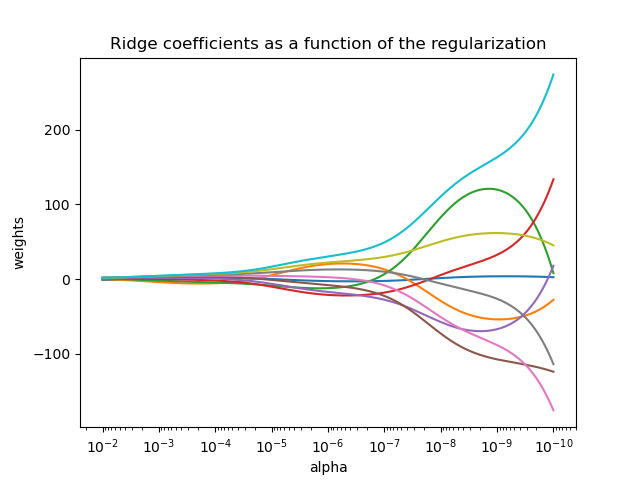
../_images/sphx_glr_plot_ridge_path_001.png

As with other linear models, Ridge will take in its fit method arrays X, y and will store the coefficients \(w\) of the linear model in its coef_ member:

>>> from sklearn import linear_model
>>> reg = linear_model.Ridge(alpha=.5)
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5)
>>> reg.coef_
array([0.34545455, 0.34545455])
>>> reg.intercept_
0.13636...

Note that the class Ridge allows for the user to specify that the solver be automatically chosen by setting solver="auto". When this option is specified, Ridge will choose between the "lbfgs", "cholesky", and "sparse_cg" solvers. Ridge will begin checking the conditions shown in the following table from top to bottom. If the condition is true, the corresponding solver is chosen.

Solver	Condition
‘lbfgs’	The `positive=True` option is specified.
‘cholesky’	The input array X is not sparse.
‘sparse_cg’	None of the above conditions are fulfilled.

1.1.2.2. Classification#

The Ridge regressor has a classifier variant: RidgeClassifier. This classifier first converts binary targets to {-1, 1} and then treats the problem as a regression task, optimizing the same objective as above. The predicted class corresponds to the sign of the regressor’s prediction. For multiclass classification, the problem is treated as multi-output regression, and the predicted class corresponds to the output with the highest value.

It might seem questionable to use a (penalized) Least Squares loss to fit a classification model instead of the more traditional logistic or hinge losses. However, in practice, all those models can lead to similar cross-validation scores in terms of accuracy or precision/recall, while the penalized least squares loss used by the RidgeClassifier allows for a very different choice of the numerical solvers with distinct computational performance profiles.

The RidgeClassifier can be significantly faster than e.g. LogisticRegression with a high number of classes because it can compute the projection matrix \((X^T X)^{-1} X^T\) only once.

This classifier is sometimes referred to as a Least Squares Support Vector Machines with a linear kernel.

Examples

1.1.2.3. Ridge Complexity#

This method has the same order of complexity as Ordinary Least Squares.

1.1.2.4. Setting the regularization parameter: leave-one-out Cross-Validation#

RidgeCV and RidgeClassifierCV implement ridge regression/classification with built-in cross-validation of the alpha parameter. They work in the same way as GridSearchCV except that it defaults to efficient Leave-One-Out cross-validation. When using the default cross-validation, alpha cannot be 0 due to the formulation used to calculate Leave-One-Out error. See [RL2007] for details.

Usage example:

>>> import numpy as np
>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=np.logspace(-6, 6, 13))
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
RidgeCV(alphas=array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
      1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06]))
>>> reg.alpha_
0.01

Specifying the value of the cv attribute will trigger the use of cross-validation with GridSearchCV, for example cv=10 for 10-fold cross-validation, rather than Leave-One-Out Cross-Validation.

1.1.3. Lasso#

The Lasso is a linear model that estimates sparse coefficients. It is useful in some contexts due to its tendency to prefer solutions with fewer non-zero coefficients, effectively reducing the number of features upon which the given solution is dependent. For this reason, Lasso and its variants are fundamental to the field of compressed sensing. Under certain conditions, it can recover the exact set of non-zero coefficients (see Compressive sensing: tomography reconstruction with L1 prior (Lasso)).

Mathematically, it consists of a linear model with an added regularization term. The objective function to minimize is:

\[\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha ||w||_1}\]

The lasso estimate thus solves the minimization of the least-squares penalty with \(\alpha ||w||_1\) added, where \(\alpha\) is a constant and \(||w||_1\) is the \(\ell_1\)-norm of the coefficient vector.

The implementation in the class Lasso uses coordinate descent as the algorithm to fit the coefficients. See Least Angle Regression for another implementation:

>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha=0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1)
>>> reg.predict([[1, 1]])
array([0.8])

The function lasso_path is useful for lower-level tasks, as it computes the coefficients along the full path of possible values.

Examples

Note

Feature selection with Lasso

As the Lasso regression yields sparse models, it can thus be used to perform feature selection, as detailed in L1-based feature selection.

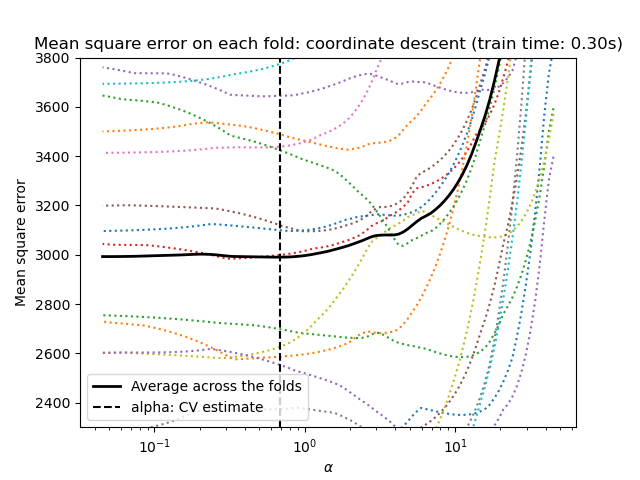
1.1.3.1. Setting regularization parameter#

The alpha parameter controls the degree of sparsity of the estimated coefficients.

1.1.3.1.1. Using cross-validation#

scikit-learn exposes objects that set the Lasso alpha parameter by cross-validation: LassoCV and LassoLarsCV. LassoLarsCV is based on the Least Angle Regression algorithm explained below.

For high-dimensional datasets with many collinear features, LassoCV is most often preferable. However, LassoLarsCV has the advantage of exploring more relevant values of alpha parameter, and if the number of samples is very small compared to the number of features, it is often faster than LassoCV.

1.1.3.1.2. Information-criteria based model selection#

Alternatively, the estimator LassoLarsIC proposes to use the Akaike information criterion (AIC) and the Bayes Information criterion (BIC). It is a computationally cheaper alternative to find the optimal value of alpha as the regularization path is computed only once instead of k+1 times when using k-fold cross-validation.

Indeed, these criteria are computed on the in-sample training set. In short, they penalize the over-optimistic scores of the different Lasso models by their flexibility (cf. to “Mathematical details” section below).

However, such criteria need a proper estimation of the degrees of freedom of the solution, are derived for large samples (asymptotic results) and assume the correct model is candidates under investigation. They also tend to break when the problem is badly conditioned (e.g. more features than samples).

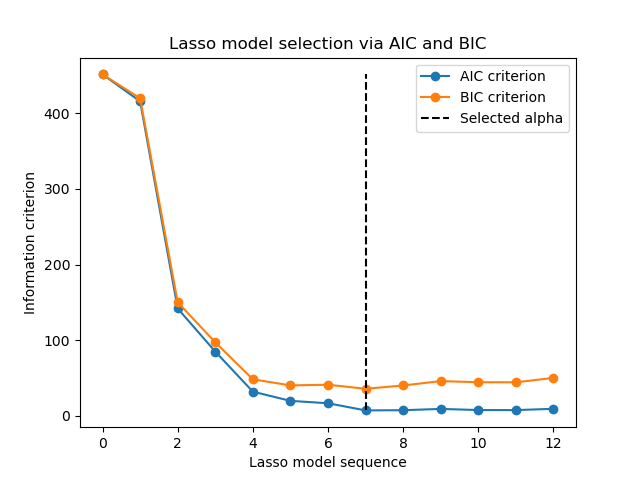
../_images/sphx_glr_plot_lasso_lars_ic_001.png

Examples

1.1.3.1.3. AIC and BIC criteria#

The definition of AIC (and thus BIC) might differ in the literature. In this section, we give more information regarding the criterion computed in scikit-learn.

1.1.3.1.4. Comparison with the regularization parameter of SVM#

The equivalence between alpha and the regularization parameter of SVM, C is given by alpha = 1 / C or alpha = 1 / (n_samples * C), depending on the estimator and the exact objective function optimized by the model.

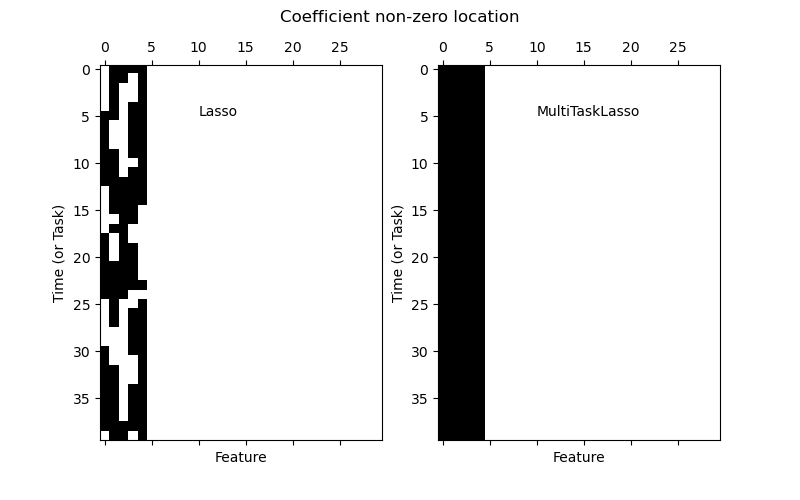
1.1.4. Multi-task Lasso#

The MultiTaskLasso is a linear model that estimates sparse coefficients for multiple regression problems jointly: y is a 2D array, of shape (n_samples, n_tasks). The constraint is that the selected features are the same for all the regression problems, also called tasks.

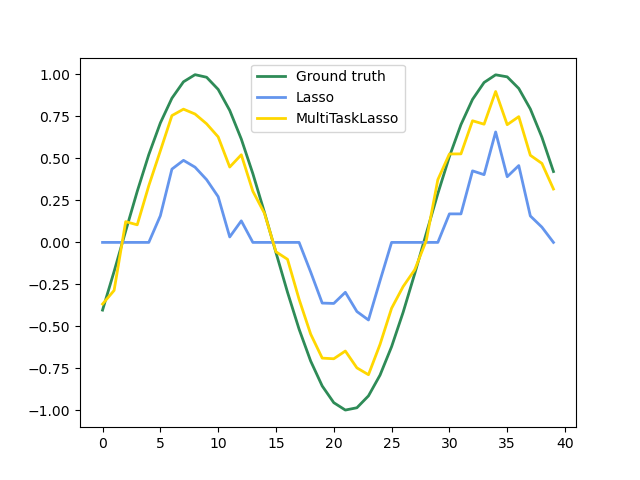
The following figure compares the location of the non-zero entries in the coefficient matrix W obtained with a simple Lasso or a MultiTaskLasso. The Lasso estimates yield scattered non-zeros while the non-zeros of the MultiTaskLasso are full columns.

Fitting a time-series model, imposing that any active feature be active at all times.

Examples

Joint feature selection with multi-task Lasso

1.1.5. Elastic-Net#

ElasticNet is a linear regression model trained with both \(\ell_1\) and \(\ell_2\)-norm regularization of the coefficients. This combination allows for learning a sparse model where few of the weights are non-zero like Lasso, while still maintaining the regularization properties of Ridge. We control the convex combination of \(\ell_1\) and \(\ell_2\) using the l1_ratio parameter.

Elastic-net is useful when there are multiple features that are correlated with one another. Lasso is likely to pick one of these at random, while elastic-net is likely to pick both.

A practical advantage of trading-off between Lasso and Ridge is that it allows Elastic-Net to inherit some of Ridge’s stability under rotation.

The objective function to minimize is in this case

\[\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha \rho ||w||_1 + \frac{\alpha(1-\rho)}{2} ||w||_2 ^ 2}\]

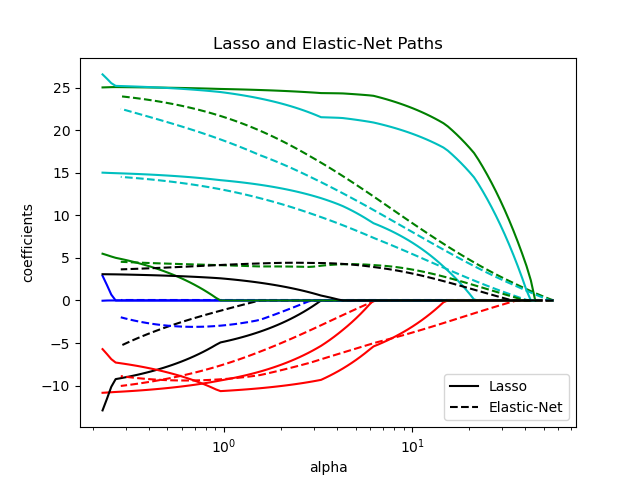
../_images/sphx_glr_plot_lasso_lasso_lars_elasticnet_path_002.png

The class ElasticNetCV can be used to set the parameters alpha (\(\alpha\)) and l1_ratio (\(\rho\)) by cross-validation.

Examples

1.1.6. Multi-task Elastic-Net#

The MultiTaskElasticNet is an elastic-net model that estimates sparse coefficients for multiple regression problems jointly: Y is a 2D array of shape (n_samples, n_tasks). The constraint is that the selected features are the same for all the regression problems, also called tasks.

Mathematically, it consists of a linear model trained with a mixed \(\ell_1\) \(\ell_2\)-norm and \(\ell_2\)-norm for regularization. The objective function to minimize is:

\[\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W - Y||_{\text{Fro}}^2 + \alpha \rho ||W||_{2 1} + \frac{\alpha(1-\rho)}{2} ||W||_{\text{Fro}}^2}\]

The implementation in the class MultiTaskElasticNet uses coordinate descent as the algorithm to fit the coefficients.

The class MultiTaskElasticNetCV can be used to set the parameters alpha (\(\alpha\)) and l1_ratio (\(\rho\)) by cross-validation.

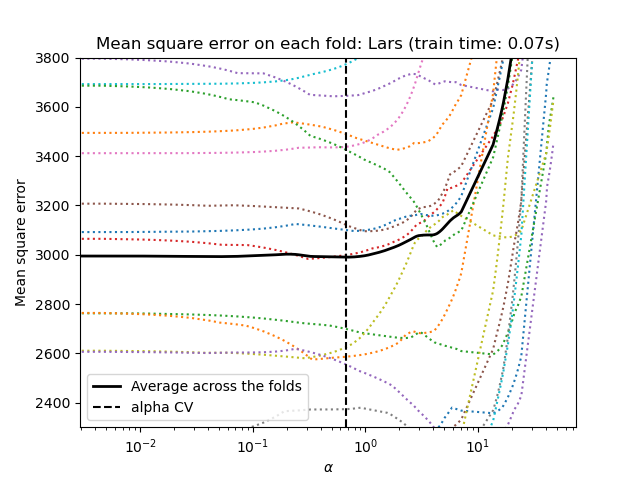
1.1.7. Least Angle Regression#

Least-angle regression (LARS) is a regression algorithm for high-dimensional data, developed by Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani. LARS is similar to forward stepwise regression. At each step, it finds the feature most correlated with the target. When there are multiple features having equal correlation, instead of continuing along the same feature, it proceeds in a direction equiangular between the features.

The advantages of LARS are:

It is numerically efficient in contexts where the number of features is significantly greater than the number of samples.
It is computationally just as fast as forward selection and has the same order of complexity as ordinary least squares.
It produces a full piecewise linear solution path, which is useful in cross-validation or similar attempts to tune the model.
If two features are almost equally correlated with the target, then their coefficients should increase at approximately the same rate. The algorithm thus behaves as intuition would expect, and also is more stable.
It is easily modified to produce solutions for other estimators, like the Lasso.

The disadvantages of the LARS method include:

Because LARS is based upon an iterative refitting of the residuals, it would appear to be especially sensitive to the effects of noise. This problem is discussed in detail by Weisberg in the discussion section of the Efron et al. (2004) Annals of Statistics article.

The LARS model can be used via the estimator Lars, or its low-level implementation lars_path or lars_path_gram.

1.1.8. LARS Lasso#

LassoLars is a lasso model implemented using the LARS algorithm, and unlike the implementation based on coordinate descent, this yields the exact solution, which is piecewise linear as a function of the norm of its coefficients.

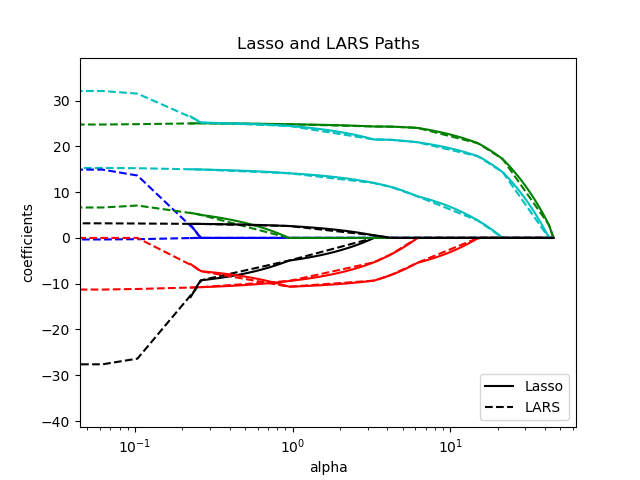
../_images/sphx_glr_plot_lasso_lasso_lars_elasticnet_path_001.png

>>> from sklearn import linear_model
>>> reg = linear_model.LassoLars(alpha=.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
LassoLars(alpha=0.1)
>>> reg.coef_
array([0.6..., 0.        ])

Examples

Lasso, Lasso-LARS, and Elastic Net paths

The Lars algorithm provides the full path of the coefficients along the regularization parameter almost for free, thus a common operation is to retrieve the path with one of the functions lars_path or lars_path_gram.

1.1.9. Orthogonal Matching Pursuit (OMP)#

OrthogonalMatchingPursuit and orthogonal_mp implement the OMP algorithm for approximating the fit of a linear model with constraints imposed on the number of non-zero coefficients (ie. the \(\ell_0\) pseudo-norm).

Being a forward feature selection method like Least Angle Regression, orthogonal matching pursuit can approximate the optimum solution vector with a fixed number of non-zero elements:

\[\underset{w}{\operatorname{arg\,min\,}} ||y - Xw||_2^2 \text{ subject to } ||w||_0 \leq n_{\text{nonzero_coefs}}\]

Alternatively, orthogonal matching pursuit can target a specific error instead of a specific number of non-zero coefficients. This can be expressed as:

\[\underset{w}{\operatorname{arg\,min\,}} ||w||_0 \text{ subject to } ||y-Xw||_2^2 \leq \text{tol}\]

OMP is based on a greedy algorithm that includes at each step the atom most highly correlated with the current residual. It is similar to the simpler matching pursuit (MP) method, but better in that at each iteration, the residual is recomputed using an orthogonal projection on the space of the previously chosen dictionary elements.

Examples

Orthogonal Matching Pursuit

1.1.10. Bayesian Regression#

Bayesian regression techniques can be used to include regularization parameters in the estimation procedure: the regularization parameter is not set in a hard sense but tuned to the data at hand.

This can be done by introducing uninformative priors over the hyper parameters of the model. The \(\ell_{2}\) regularization used in Ridge regression and classification is equivalent to finding a maximum a posteriori estimation under a Gaussian prior over the coefficients \(w\) with precision \(\lambda^{-1}\). Instead of setting lambda manually, it is possible to treat it as a random variable to be estimated from the data.

To obtain a fully probabilistic model, the output \(y\) is assumed to be Gaussian distributed around \(X w\):

\[p(y|X,w,\alpha) = \mathcal{N}(y|X w,\alpha^{-1})\]

where \(\alpha\) is again treated as a random variable that is to be estimated from the data.

The advantages of Bayesian Regression are:

It adapts to the data at hand.
It can be used to include regularization parameters in the estimation procedure.

The disadvantages of Bayesian regression include:

Inference of the model can be time consuming.

1.1.10.1. Bayesian Ridge Regression#

BayesianRidge estimates a probabilistic model of the regression problem as described above. The prior for the coefficient \(w\) is given by a spherical Gaussian:

\[p(w|\lambda) = \mathcal{N}(w|0,\lambda^{-1}\mathbf{I}_{p})\]

The priors over \(\alpha\) and \(\lambda\) are chosen to be gamma distributions, the conjugate prior for the precision of the Gaussian. The resulting model is called Bayesian Ridge Regression, and is similar to the classical Ridge.

The parameters \(w\), \(\alpha\) and \(\lambda\) are estimated jointly during the fit of the model, the regularization parameters \(\alpha\) and \(\lambda\) being estimated by maximizing the log marginal likelihood. The scikit-learn implementation is based on the algorithm described in Appendix A of (Tipping, 2001) where the update of the parameters \(\alpha\) and \(\lambda\) is done as suggested in (MacKay, 1992). The initial value of the maximization procedure can be set with the hyperparameters alpha_init and lambda_init.

There are four more hyperparameters, \(\alpha_1\), \(\alpha_2\), \(\lambda_1\) and \(\lambda_2\) of the gamma prior distributions over \(\alpha\) and \(\lambda\). These are usually chosen to be non-informative. By default \(\alpha_1 = \alpha_2 = \lambda_1 = \lambda_2 = 10^{-6}\).

Bayesian Ridge Regression is used for regression:

>>> from sklearn import linear_model
>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]
>>> Y = [0., 1., 2., 3.]
>>> reg = linear_model.BayesianRidge()
>>> reg.fit(X, Y)
BayesianRidge()

After being fitted, the model can then be used to predict new values:

>>> reg.predict([[1, 0.]])
array([0.50000013])

The coefficients \(w\) of the model can be accessed:

>>> reg.coef_
array([0.49999993, 0.49999993])

Due to the Bayesian framework, the weights found are slightly different to the ones found by Ordinary Least Squares. However, Bayesian Ridge Regression is more robust to ill-posed problems.

Examples

Curve Fitting with Bayesian Ridge Regression

1.1.10.2. Automatic Relevance Determination - ARD#

The Automatic Relevance Determination (as being implemented in ARDRegression) is a kind of linear model which is very similar to the Bayesian Ridge Regression, but that leads to sparser coefficients \(w\) [1] [2].

ARDRegression poses a different prior over \(w\): it drops the spherical Gaussian distribution for a centered elliptic Gaussian distribution. This means each coefficient \(w_{i}\) can itself be drawn from a Gaussian distribution, centered on zero and with a precision \(\lambda_{i}\):

\[p(w|\lambda) = \mathcal{N}(w|0,A^{-1})\]

with \(A\) being a positive definite diagonal matrix and \(\text{diag}(A) = \lambda = \{\lambda_{1},...,\lambda_{p}\}\).

In contrast to the Bayesian Ridge Regression, each coordinate of \(w_{i}\) has its own standard deviation \(\frac{1}{\lambda_i}\). The prior over all \(\lambda_i\) is chosen to be the same gamma distribution given by the hyperparameters \(\lambda_1\) and \(\lambda_2\).

ARD is also known in the literature as Sparse Bayesian Learning and Relevance Vector Machine [3] [4]. For a worked-out comparison between ARD and Bayesian Ridge Regression, see the example below.

Examples

Comparing Linear Bayesian Regressors

References

1.1.11. Logistic regression#

The logistic regression is implemented in LogisticRegression. Despite its name, it is implemented as a linear model for classification rather than regression in terms of the scikit-learn/ML nomenclature. The logistic regression is also known in the literature as logit regression, maximum-entropy classification (MaxEnt) or the log-linear classifier. In this model, the probabilities describing the possible outcomes of a single trial are modeled using a logistic function.

This implementation can fit binary, One-vs-Rest, or multinomial logistic regression with optional \(\ell_1\), \(\ell_2\) or Elastic-Net regularization.

Note

Regularization

Regularization is applied by default, which is common in machine learning but not in statistics. Another advantage of regularization is that it improves numerical stability. No regularization amounts to setting C to a very high value.

Note

Logistic Regression as a special case of the Generalized Linear Models (GLM)

Logistic regression is a special case of Generalized Linear Models with a Binomial / Bernoulli conditional distribution and a Logit link. The numerical output of the logistic regression, which is the predicted probability, can be used as a classifier by applying a threshold (by default 0.5) to it. This is how it is implemented in scikit-learn, so it expects a categorical target, making the Logistic Regression a classifier.

Examples

1.1.11.1. Binary Case#

For notational ease, we assume that the target \(y_i\) takes values in the set \(\{0, 1\}\) for data point \(i\). Once fitted, the predict_proba method of LogisticRegression predicts the probability of the positive class \(P(y_i=1|X_i)\) as

\[\hat{p}(X_i) = \operatorname{expit}(X_i w + w_0) = \frac{1}{1 + \exp(-X_i w - w_0)}.\]

As an optimization problem, binary class logistic regression with regularization term \(r(w)\) minimizes the following cost function:

(1)#\[\min_{w} \frac{1}{S}\sum_{i=1}^n s_i \left(-y_i \log(\hat{p}(X_i)) - (1 - y_i) \log(1 - \hat{p}(X_i))\right) + \frac{r(w)}{S C}\,,\]

where \({s_i}\) corresponds to the weights assigned by the user to a specific training sample (the vector \(s\) is formed by element-wise multiplication of the class weights and sample weights), and the sum \(S = \sum_{i=1}^n s_i\).

We currently provide four choices for the regularization term \(r(w)\) via the penalty argument:

penalty	\(r(w)\)
`None`	\(0\)
\(\ell_1\)	\(\\|w\\|_1\)
\(\ell_2\)	\(\frac{1}{2}\\|w\\|_2^2 = \frac{1}{2}w^T w\)
`ElasticNet`	\(\frac{1 - \rho}{2}w^T w + \rho \\|w\\|_1\)

For ElasticNet, \(\rho\) (which corresponds to the l1_ratio parameter) controls the strength of \(\ell_1\) regularization vs. \(\ell_2\) regularization. Elastic-Net is equivalent to \(\ell_1\) when \(\rho = 1\) and equivalent to \(\ell_2\) when \(\rho=0\).

Note that the scale of the class weights and the sample weights will influence the optimization problem. For instance, multiplying the sample weights by a constant \(b>0\) is equivalent to multiplying the (inverse) regularization strength C by \(b\).

1.1.11.2. Multinomial Case#

The binary case can be extended to \(K\) classes leading to the multinomial logistic regression, see also log-linear model.

Note

It is possible to parameterize a \(K\)-class classification model using only \(K-1\) weight vectors, leaving one class probability fully determined by the other class probabilities by leveraging the fact that all class probabilities must sum to one. We deliberately choose to overparameterize the model using \(K\) weight vectors for ease of implementation and to preserve the symmetrical inductive bias regarding ordering of classes, see [16]. This effect becomes especially important when using regularization. The choice of overparameterization can be detrimental for unpenalized models since then the solution may not be unique, as shown in [16].

Mathematical details#

Let \(y_i \in {1, \ldots, K}\) be the label (ordinal) encoded target variable for observation \(i\). Instead of a single coefficient vector, we now have a matrix of coefficients \(W\) where each row vector \(W_k\) corresponds to class \(k\). We aim at predicting the class probabilities \(P(y_i=k|X_i)\) via predict_proba as:

\[\hat{p}_k(X_i) = \frac{\exp(X_i W_k + W_{0, k})}{\sum_{l=0}^{K-1} \exp(X_i W_l + W_{0, l})}.\]

The objective for the optimization becomes

\[\min_W -\frac{1}{S}\sum_{i=1}^n \sum_{k=0}^{K-1} s_{ik} [y_i = k] \log(\hat{p}_k(X_i)) + \frac{r(W)}{S C}\,,\]

where \([P]\) represents the Iverson bracket which evaluates to \(0\) if \(P\) is false, otherwise it evaluates to \(1\).

Again, \(s_{ik}\) are the weights assigned by the user (multiplication of sample weights and class weights) with their sum \(S = \sum_{i=1}^n \sum_{k=0}^{K-1} s_{ik}\).

We currently provide four choices for the regularization term \(r(W)\) via the penalty argument, where \(m\) is the number of features:

penalty	\(r(W)\)
`None`	\(0\)
\(\ell_1\)	\(\\|W\\|_{1,1} = \sum_{i=1}^m\sum_{j=1}^{K}\|W_{i,j}\|\)
\(\ell_2\)	\(\frac{1}{2}\\|W\\|_F^2 = \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^{K} W_{i,j}^2\)
`ElasticNet`	\(\frac{1 - \rho}{2}\\|W\\|_F^2 + \rho \\|W\\|_{1,1}\)

1.1.11.3. Solvers#

The solvers implemented in the class LogisticRegression are “lbfgs”, “liblinear”, “newton-cg”, “newton-cholesky”, “sag” and “saga”:

The following table summarizes the penalties and multinomial multiclass supported by each solver:

	Solvers
Penalties	‘lbfgs’	‘liblinear’	‘newton-cg’	‘newton-cholesky’	‘sag’	‘saga’
L2 penalty	yes	no	yes	no	yes	yes
L1 penalty	no	yes	no	no	no	yes
Elastic-Net (L1 + L2)	no	no	no	no	no	yes
No penalty (‘none’)	yes	no	yes	yes	yes	yes
Multiclass support
multinomial multiclass	yes	no	yes	no	yes	yes
Behaviors
Penalize the intercept (bad)	no	yes	no	no	no	no
Faster for large datasets	no	no	no	no	yes	yes
Robust to unscaled datasets	yes	yes	yes	yes	no	no

The “lbfgs” solver is used by default for its robustness. For large datasets the “saga” solver is usually faster. For large dataset, you may also consider using SGDClassifier with loss="log_loss", which might be even faster but requires more tuning.

1.1.11.3.1. Differences between solvers#

There might be a difference in the scores obtained between LogisticRegression with solver=liblinear or LinearSVC and the external liblinear library directly, when fit_intercept=False and the fit coef_ (or) the data to be predicted are zeroes. This is because for the sample(s) with decision_function zero, LogisticRegression and LinearSVC predict the negative class, while liblinear predicts the positive class. Note that a model with fit_intercept=False and having many samples with decision_function zero, is likely to be a underfit, bad model and you are advised to set fit_intercept=True and increase the intercept_scaling.

Solvers’ details#

The solver “liblinear” uses a coordinate descent (CD) algorithm, and relies on the excellent C++ LIBLINEAR library, which is shipped with scikit-learn. However, the CD algorithm implemented in liblinear cannot learn a true multinomial (multiclass) model; instead, the optimization problem is decomposed in a “one-vs-rest” fashion so separate binary classifiers are trained for all classes. This happens under the hood, so LogisticRegression instances using this solver behave as multiclass classifiers. For \(\ell_1\) regularization sklearn.svm.l1_min_c allows to calculate the lower bound for C in order to get a non “null” (all feature weights to zero) model.
The “lbfgs”, “newton-cg” and “sag” solvers only support \(\ell_2\) regularization or no regularization, and are found to converge faster for some high-dimensional data. Setting multi_class to “multinomial” with these solvers learns a true multinomial logistic regression model [5], which means that its probability estimates should be better calibrated than the default “one-vs-rest” setting.
The “sag” solver uses Stochastic Average Gradient descent [6]. It is faster than other solvers for large datasets, when both the number of samples and the number of features are large.
The “saga” solver [7] is a variant of “sag” that also supports the non-smooth penalty="l1". This is therefore the solver of choice for sparse multinomial logistic regression. It is also the only solver that supports penalty="elasticnet".
The “lbfgs” is an optimization algorithm that approximates the Broyden–Fletcher–Goldfarb–Shanno algorithm [8], which belongs to quasi-Newton methods. As such, it can deal with a wide range of different training data and is therefore the default solver. Its performance, however, suffers on poorly scaled datasets and on datasets with one-hot encoded categorical features with rare categories.
The “newton-cholesky” solver is an exact Newton solver that calculates the hessian matrix and solves the resulting linear system. It is a very good choice for n_samples >> n_features, but has a few shortcomings: Only \(\ell_2\) regularization is supported. Furthermore, because the hessian matrix is explicitly computed, the memory usage has a quadratic dependency on n_features as well as on n_classes. As a consequence, only the one-vs-rest scheme is implemented for the multiclass case.

For a comparison of some of these solvers, see [9].

References

Note

Feature selection with sparse logistic regression

A logistic regression with \(\ell_1\) penalty yields sparse models, and can thus be used to perform feature selection, as detailed in L1-based feature selection.

Note

P-value estimation

It is possible to obtain the p-values and confidence intervals for coefficients in cases of regression without penalization. The statsmodels package natively supports this. Within sklearn, one could use bootstrapping instead as well.

LogisticRegressionCV implements Logistic Regression with built-in cross-validation support, to find the optimal C and l1_ratio parameters according to the scoring attribute. The “newton-cg”, “sag”, “saga” and “lbfgs” solvers are found to be faster for high-dimensional dense data, due to warm-starting (see Glossary).

1.1.12. Generalized Linear Models#

Generalized Linear Models (GLM) extend linear models in two ways [10]. First, the predicted values \(\hat{y}\) are linked to a linear combination of the input variables \(X\) via an inverse link function \(h\) as

\[\hat{y}(w, X) = h(Xw).\]

Secondly, the squared loss function is replaced by the unit deviance \(d\) of a distribution in the exponential family (or more precisely, a reproductive exponential dispersion model (EDM) [11]).

The minimization problem becomes:

\[\min_{w} \frac{1}{2 n_{\text{samples}}} \sum_i d(y_i, \hat{y}_i) + \frac{\alpha}{2} ||w||_2^2,\]

where \(\alpha\) is the L2 regularization penalty. When sample weights are provided, the average becomes a weighted average.

The following table lists some specific EDMs and their unit deviance :

Distribution	Target Domain	Unit Deviance \(d(y, \hat{y})\)
Normal	\(y \in (-\infty, \infty)\)	\((y-\hat{y})^2\)
Bernoulli	\(y \in \{0, 1\}\)	\(2({y}\log\frac{y}{\hat{y}}+({1}-{y})\log\frac{{1}-{y}}{{1}-\hat{y}})\)
Categorical	\(y \in \{0, 1, ..., k\}\)	\(2\sum_{i \in \{0, 1, ..., k\}} I(y = i) y_\text{i}\log\frac{I(y = i)}{\hat{I(y = i)}}\)
Poisson	\(y \in [0, \infty)\)	\(2(y\log\frac{y}{\hat{y}}-y+\hat{y})\)
Gamma	\(y \in (0, \infty)\)	\(2(\log\frac{\hat{y}}{y}+\frac{y}{\hat{y}}-1)\)
Inverse Gaussian	\(y \in (0, \infty)\)	\(\frac{(y-\hat{y})^2}{y\hat{y}^2}\)

The Probability Density Functions (PDF) of these distributions are illustrated in the following figure,

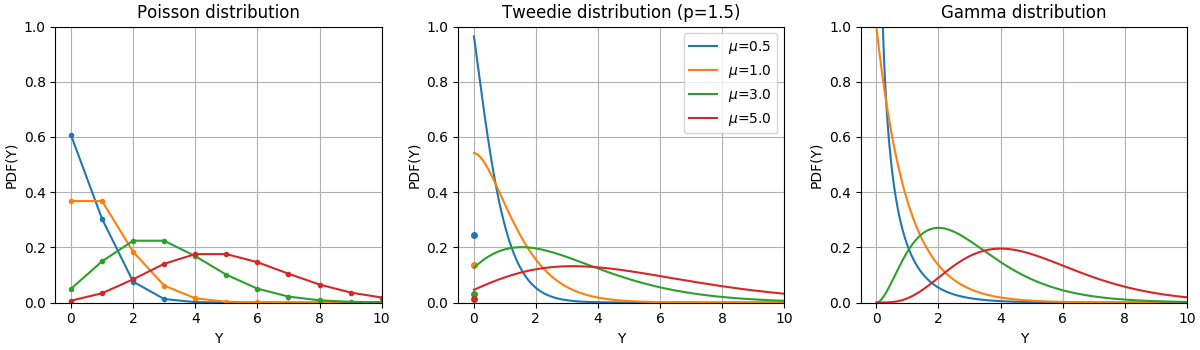
../_images/poisson_gamma_tweedie_distributions.png — PDF of a random variable Y following Poisson, Tweedie (power=1.5) and Gamma distributions with different mean values (\(\mu\)). Observe the point mass at \(Y=0\) for the Poisson distribution and the Tweedie (power=1.5) distribution, but not for the Gamma distribution which has a strictly positive target domain.#

The Bernoulli distribution is a discrete probability distribution modelling a Bernoulli trial - an event that has only two mutually exclusive outcomes. The Categorical distribution is a generalization of the Bernoulli distribution for a categorical random variable. While a random variable in a Bernoulli distribution has two possible outcomes, a Categorical random variable can take on one of K possible categories, with the probability of each category specified separately.

The choice of the distribution depends on the problem at hand:

If the target values \(y\) are counts (non-negative integer valued) or relative frequencies (non-negative), you might use a Poisson distribution with a log-link.
If the target values are positive valued and skewed, you might try a Gamma distribution with a log-link.
If the target values seem to be heavier tailed than a Gamma distribution, you might try an Inverse Gaussian distribution (or even higher variance powers of the Tweedie family).
If the target values \(y\) are probabilities, you can use the Bernoulli distribution. The Bernoulli distribution with a logit link can be used for binary classification. The Categorical distribution with a softmax link can be used for multiclass classification.

References

1.1.12.1. Usage#

TweedieRegressor implements a generalized linear model for the Tweedie distribution, that allows to model any of the above mentioned distributions using the appropriate power parameter. In particular:

power = 0: Normal distribution. Specific estimators such as Ridge, ElasticNet are generally more appropriate in this case.
power = 1: Poisson distribution. PoissonRegressor is exposed for convenience. However, it is strictly equivalent to TweedieRegressor(power=1, link='log').
power = 2: Gamma distribution. GammaRegressor is exposed for convenience. However, it is strictly equivalent to TweedieRegressor(power=2, link='log').
power = 3: Inverse Gaussian distribution.

The link function is determined by the link parameter.

Usage example:

>>> from sklearn.linear_model import TweedieRegressor
>>> reg = TweedieRegressor(power=1, alpha=0.5, link='log')
>>> reg.fit([[0, 0], [0, 1], [2, 2]], [0, 1, 2])
TweedieRegressor(alpha=0.5, link='log', power=1)
>>> reg.coef_
array([0.2463..., 0.4337...])
>>> reg.intercept_
-0.7638...

Examples

1.1.13. Stochastic Gradient Descent - SGD#

Stochastic gradient descent is a simple yet very efficient approach to fit linear models. It is particularly useful when the number of samples (and the number of features) is very large. The partial_fit method allows online/out-of-core learning.

The classes SGDClassifier and SGDRegressor provide functionality to fit linear models for classification and regression using different (convex) loss functions and different penalties. E.g., with loss="log", SGDClassifier fits a logistic regression model, while with loss="hinge" it fits a linear support vector machine (SVM).

You can refer to the dedicated Stochastic Gradient Descent documentation section for more details.

1.1.14. Perceptron#

The Perceptron is another simple classification algorithm suitable for large scale learning. By default:

It does not require a learning rate.
It is not regularized (penalized).
It updates its model only on mistakes.

The last characteristic implies that the Perceptron is slightly faster to train than SGD with the hinge loss and that the resulting models are sparser.

In fact, the Perceptron is a wrapper around the SGDClassifier class using a perceptron loss and a constant learning rate. Refer to mathematical section of the SGD procedure for more details.

1.1.15. Passive Aggressive Algorithms#

The passive-aggressive algorithms are a family of algorithms for large-scale learning. They are similar to the Perceptron in that they do not require a learning rate. However, contrary to the Perceptron, they include a regularization parameter C.

For classification, PassiveAggressiveClassifier can be used with loss='hinge' (PA-I) or loss='squared_hinge' (PA-II). For regression, PassiveAggressiveRegressor can be used with loss='epsilon_insensitive' (PA-I) or loss='squared_epsilon_insensitive' (PA-II).

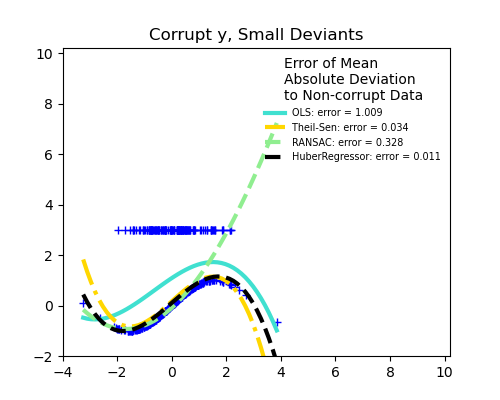
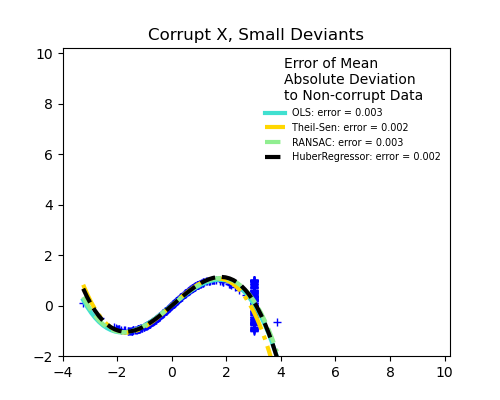
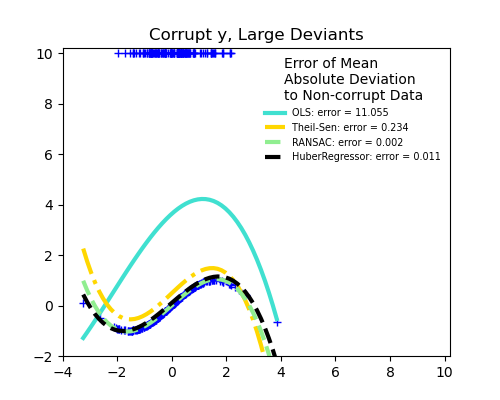
1.1.16. Robustness regression: outliers and modeling errors#

Robust regression aims to fit a regression model in the presence of corrupt data: either outliers, or error in the model.

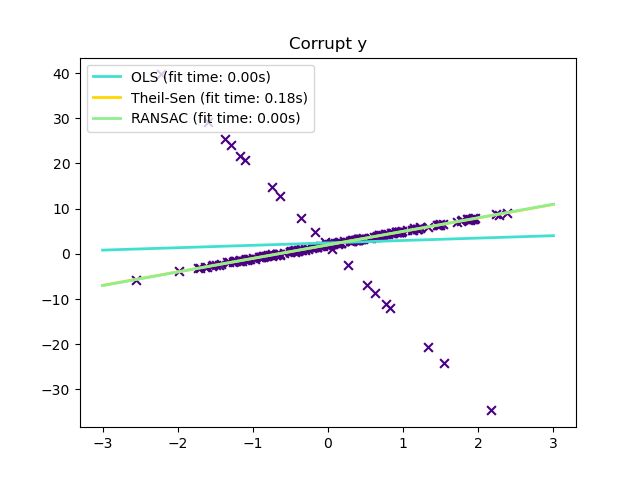
../_images/sphx_glr_plot_theilsen_001.png

1.1.16.1. Different scenario and useful concepts#

There are different things to keep in mind when dealing with data corrupted by outliers:

Outliers in X or in y?

Outliers in the y direction

Outliers in the X direction
Fraction of outliers versus amplitude of error

The number of outlying points matters, but also how much they are outliers.

Small outliers

Large outliers

An important notion of robust fitting is that of breakdown point: the fraction of data that can be outlying for the fit to start missing the inlying data.

Note that in general, robust fitting in high-dimensional setting (large n_features) is very hard. The robust models here will probably not work in these settings.

1.1.16.2. RANSAC: RANdom SAmple Consensus#

RANSAC (RANdom SAmple Consensus) fits a model from random subsets of inliers from the complete data set.

RANSAC is a non-deterministic algorithm producing only a reasonable result with a certain probability, which is dependent on the number of iterations (see max_trials parameter). It is typically used for linear and non-linear regression problems and is especially popular in the field of photogrammetric computer vision.

The algorithm splits the complete input sample data into a set of inliers, which may be subject to noise, and outliers, which are e.g. caused by erroneous measurements or invalid hypotheses about the data. The resulting model is then estimated only from the determined inliers.

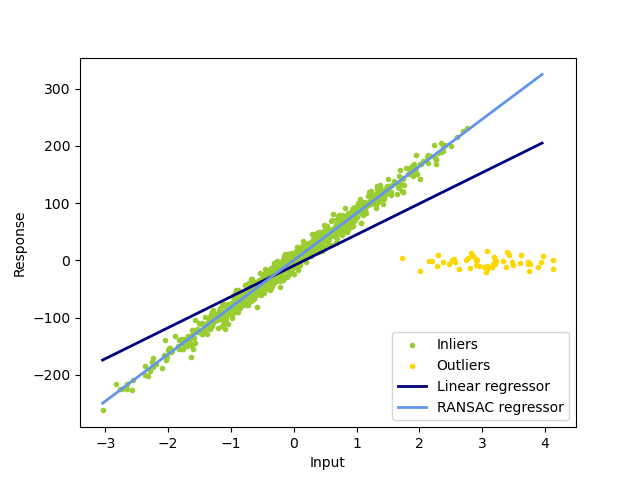
Examples

1.1.16.3. Theil-Sen estimator: generalized-median-based estimator#

The TheilSenRegressor estimator uses a generalization of the median in multiple dimensions. It is thus robust to multivariate outliers. Note however that the robustness of the estimator decreases quickly with the dimensionality of the problem. It loses its robustness properties and becomes no better than an ordinary least squares in high dimension.

Examples

1.1.16.4. Huber Regression#

The HuberRegressor is different from Ridge because it applies a linear loss to samples that are defined as outliers by the epsilon parameter. A sample is classified as an inlier if the absolute error of that sample is lesser than the threshold epsilon. It differs from TheilSenRegressor and RANSACRegressor because it does not ignore the effect of the outliers but gives a lesser weight to them.

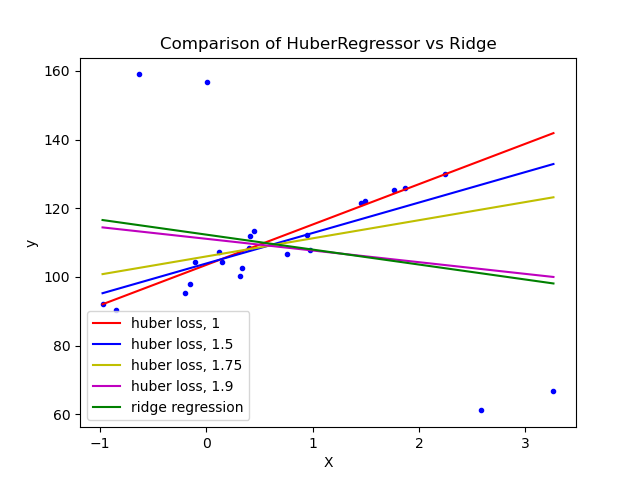
../_images/sphx_glr_plot_huber_vs_ridge_001.png

Examples

HuberRegressor vs Ridge on dataset with strong outliers

The HuberRegressor differs from using SGDRegressor with loss set to huber in the following ways.

HuberRegressor is scaling invariant. Once epsilon is set, scaling X and y down or up by different values would produce the same robustness to outliers as before. as compared to SGDRegressor where epsilon has to be set again when X and y are scaled.
HuberRegressor should be more efficient to use on data with small number of samples while SGDRegressor needs a number of passes on the training data to produce the same robustness.

Note that this estimator is different from the R implementation of Robust Regression because the R implementation does a weighted least squares implementation with weights given to each sample on the basis of how much the residual is greater than a certain threshold.

1.1.17. Quantile Regression#

Quantile regression estimates the median or other quantiles of \(y\) conditional on \(X\), while ordinary least squares (OLS) estimates the conditional mean.

Quantile regression may be useful if one is interested in predicting an interval instead of point prediction. Sometimes, prediction intervals are calculated based on the assumption that prediction error is distributed normally with zero mean and constant variance. Quantile regression provides sensible prediction intervals even for errors with non-constant (but predictable) variance or non-normal distribution.

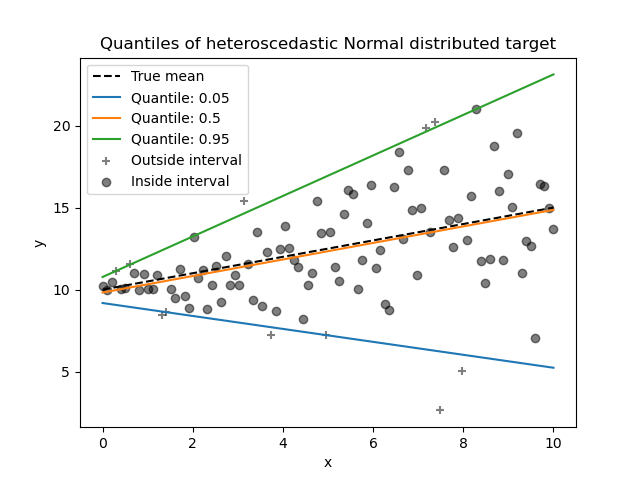
../_images/sphx_glr_plot_quantile_regression_002.png

Based on minimizing the pinball loss, conditional quantiles can also be estimated by models other than linear models. For example, GradientBoostingRegressor can predict conditional quantiles if its parameter loss is set to "quantile" and parameter alpha is set to the quantile that should be predicted. See the example in Prediction Intervals for Gradient Boosting Regression.

Most implementations of quantile regression are based on linear programming problem. The current implementation is based on scipy.optimize.linprog.

Examples

Quantile regression

1.1.18. Polynomial regression: extending linear models with basis functions#

One common pattern within machine learning is to use linear models trained on nonlinear functions of the data. This approach maintains the generally fast performance of linear methods, while allowing them to fit a much wider range of data.

Here is an example of applying this idea to one-dimensional data, using polynomial features of varying degrees:

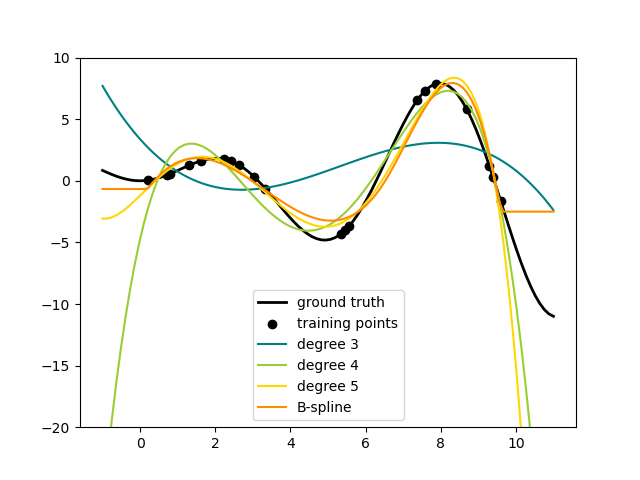
../_images/sphx_glr_plot_polynomial_interpolation_001.png

This figure is created using the PolynomialFeatures transformer, which transforms an input data matrix into a new data matrix of a given degree. It can be used as follows:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

The features of X have been transformed from \([x_1, x_2]\) to \([1, x_1, x_2, x_1^2, x_1 x_2, x_2^2]\), and can now be used within any linear model.

This sort of preprocessing can be streamlined with the Pipeline tools. A single object representing a simple polynomial regression can be created and used as follows:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
...                   ('linear', LinearRegression(fit_intercept=False))])
>>> # fit to an order-3 polynomial data
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2.,  1., -1.])

The linear model trained on polynomial features is able to exactly recover the input polynomial coefficients.

In some cases it’s not necessary to include higher powers of any single feature, but only the so-called interaction features that multiply together at most \(d\) distinct features. These can be gotten from PolynomialFeatures with the setting interaction_only=True.

For example, when dealing with boolean features, \(x_i^n = x_i\) for all \(n\) and is therefore useless; but \(x_i x_j\) represents the conjunction of two booleans. This way, we can solve the XOR problem with a linear classifier:

>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
       [1, 0, 1, 0],
       [1, 1, 0, 0],
       [1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, max_iter=10, tol=None,
...                  shuffle=False).fit(X, y)

And the classifier “predictions” are perfect:

>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0