1.5. Stochastic Gradient Descent#

Stochastic Gradient Descent (SGD) is a simple yet very efficient approach to fitting linear classifiers and regressors under convex loss functions such as (linear) Support Vector Machines and Logistic Regression. Even though SGD has been around in the machine learning community for a long time, it has received a considerable amount of attention just recently in the context of large-scale learning.

SGD has been successfully applied to large-scale and sparse machine learning problems often encountered in text classification and natural language processing. Given that the data is sparse, the classifiers in this module easily scale to problems with more than 10^5 training examples and more than 10^5 features.

Strictly speaking, SGD is merely an optimization technique and does not correspond to a specific family of machine learning models. It is only a way to train a model. Often, an instance of SGDClassifier or SGDRegressor will have an equivalent estimator in the scikit-learn API, potentially using a different optimization technique. For example, using SGDClassifier(loss='log_loss') results in logistic regression, i.e. a model equivalent to LogisticRegression which is fitted via SGD instead of being fitted by one of the other solvers in LogisticRegression. Similarly, SGDRegressor(loss='squared_error', penalty='l2') and Ridge solve the same optimization problem, via different means.

The advantages of Stochastic Gradient Descent are:

  • Efficiency.

  • Ease of implementation (lots of opportunities for code tuning).

The disadvantages of Stochastic Gradient Descent include:

  • SGD requires a number of hyperparameters such as the regularization parameter and the number of iterations.

  • SGD is sensitive to feature scaling.

Warning

Make sure you permute (shuffle) your training data before fitting the model or use shuffle=True to shuffle after each iteration (used by default). Also, ideally, features should be standardized using e.g. make_pipeline(StandardScaler(), SGDClassifier()) (see Pipelines).

1.5.1. Classification#

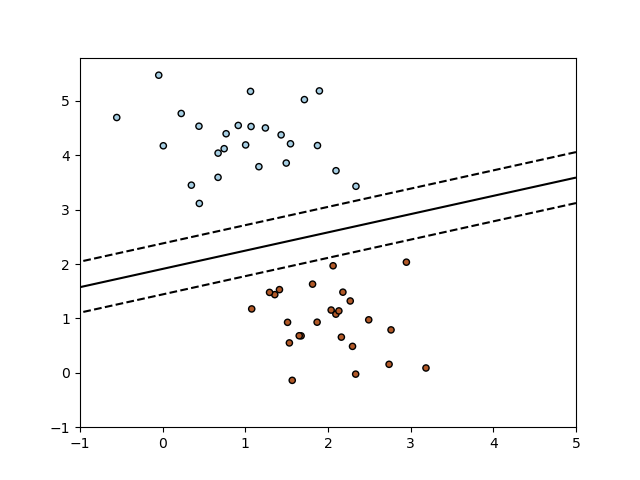
The class SGDClassifier implements a plain stochastic gradient descent learning routine which supports different loss functions and penalties for classification. Below is the decision boundary of a SGDClassifier trained with the hinge loss, equivalent to a linear SVM.

../_images/sphx_glr_plot_sgd_separating_hyperplane_001.png

As other classifiers, SGD has to be fitted with two arrays: an array X of shape (n_samples, n_features) holding the training samples, and an array y of shape (n_samples,) holding the target values (class labels) for the training samples:

>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
>>> clf.fit(X, y)
SGDClassifier(max_iter=5)

After being fitted, the model can then be used to predict new values:

>>> clf.predict([[2., 2.]])
array([1])

SGD fits a linear model to the training data. The coef_ attribute holds the model parameters:

>>> clf.coef_
array([[9.9..., 9.9...]])

The intercept_ attribute holds the intercept (aka offset or bias):

>>> clf.intercept_
array([-9.9...])

Whether or not the model should use an intercept, i.e. a biased hyperplane, is controlled by the parameter fit_intercept.

The signed distance to the hyperplane (computed as the dot product between the coefficients and the input sample, plus the intercept) is given by SGDClassifier.decision_function:

>>> clf.decision_function([[2., 2.]])
array([29.6...])

The concrete loss function can be set via the loss parameter. SGDClassifier supports the following loss functions:

  • loss="hinge": (soft-margin) linear Support Vector Machine,

  • loss="modified_huber": smoothed hinge loss,

  • loss="log_loss": logistic regression,

  • and all regression losses below. In this case the target is encoded as -1 or 1, and the problem is treated as a regression problem. The predicted class then correspond to the sign of the predicted target.

Please refer to the mathematical section below for formulas. The first two loss functions are lazy, they only update the model parameters if an example violates the margin constraint, which makes training very efficient and may result in sparser models (i.e. with more zero coefficients), even when L2 penalty is used.

Using loss="log_loss" or loss="modified_huber" enables the predict_proba method, which gives a vector of probability estimates \(P(y|x)\) per sample \(x\):

>>> clf = SGDClassifier(loss="log_loss", max_iter=5).fit(X, y)
>>> clf.predict_proba([[1., 1.]]) 
array([[0.00..., 0.99...]])

The concrete penalty can be set via the penalty parameter. SGD supports the following penalties:

  • penalty="l2": L2 norm penalty on coef_.

  • penalty="l1": L1 norm penalty on coef_.

  • penalty="elasticnet": Convex combination of L2 and L1; (1 - l1_ratio) * L2 + l1_ratio * L1.

The default setting is penalty="l2". The L1 penalty leads to sparse solutions, driving most coefficients to zero. The Elastic Net [11] solves some deficiencies of the L1 penalty in the presence of highly correlated attributes. The parameter l1_ratio controls the convex combination of L1 and L2 penalty.

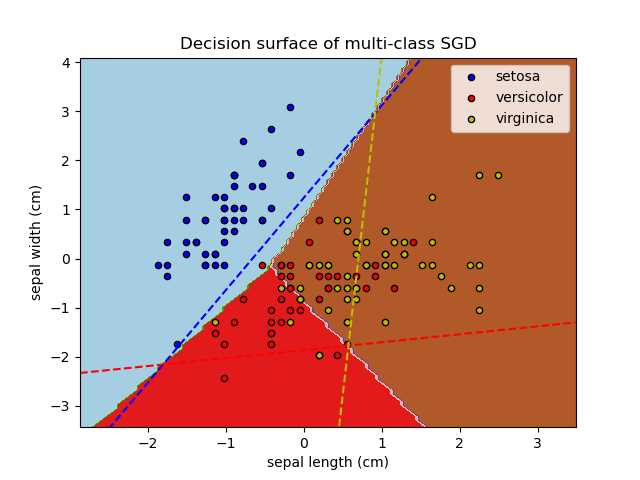
SGDClassifier supports multi-class classification by combining multiple binary classifiers in a “one versus all” (OVA) scheme. For each of the \(K\) classes, a binary classifier is learned that discriminates between that and all other \(K-1\) classes. At testing time, we compute the confidence score (i.e. the signed distances to the hyperplane) for each classifier and choose the class with the highest confidence. The Figure below illustrates the OVA approach on the iris dataset. The dashed lines represent the three OVA classifiers; the background colors show the decision surface induced by the three classifiers.

../_images/sphx_glr_plot_sgd_iris_001.png

In the case of multi-class classification coef_ is a two-dimensional array of shape (n_classes, n_features) and intercept_ is a one-dimensional array of shape (n_classes,). The i-th row of coef_ holds the weight vector of the OVA classifier for the i-th class; classes are indexed in ascending order (see attribute classes_). Note that, in principle, since they allow to create a probability model, loss="log_loss" and loss="modified_huber" are more suitable for one-vs-all classification.

SGDClassifier supports both weighted classes and weighted instances via the fit parameters class_weight and sample_weight. See the examples below and the docstring of SGDClassifier.fit for further information.

SGDClassifier supports averaged SGD (ASGD) [10]. Averaging can be enabled by setting average=True. ASGD performs the same updates as the regular SGD (see Mathematical formulation), but instead of using the last value of the coefficients as the coef_ attribute (i.e. the values of the last update), coef_ is set instead to the average value of the coefficients across all updates. The same is done for the intercept_ attribute. When using ASGD the learning rate can be larger and even constant, leading on some datasets to a speed up in training time.

For classification with a logistic loss, another variant of SGD with an averaging strategy is available with Stochastic Average Gradient (SAG) algorithm, available as a solver in LogisticRegression.

Examples

1.5.2. Regression#

The class SGDRegressor implements a plain stochastic gradient descent learning routine which supports different loss functions and penalties to fit linear regression models. SGDRegressor is well suited for regression problems with a large number of training samples (> 10.000), for other problems we recommend Ridge, Lasso, or ElasticNet.

The concrete loss function can be set via the loss parameter. SGDRegressor supports the following loss functions:

  • loss="squared_error": Ordinary least squares,

  • loss="huber": Huber loss for robust regression,

  • loss="epsilon_insensitive": linear Support Vector Regression.

Please refer to the mathematical section below for formulas. The Huber and epsilon-insensitive loss functions can be used for robust regression. The width of the insensitive region has to be specified via the parameter epsilon. This parameter depends on the scale of the target variables.

The penalty parameter determines the regularization to be used (see description above in the classification section).

SGDRegressor also supports averaged SGD [10] (here again, see description above in the classification section).

For regression with a squared loss and a l2 penalty, another variant of SGD with an averaging strategy is available with Stochastic Average Gradient (SAG) algorithm, available as a solver in Ridge.

1.5.3. Online One-Class SVM#

The class sklearn.linear_model.SGDOneClassSVM implements an online linear version of the One-Class SVM using a stochastic gradient descent. Combined with kernel approximation techniques, sklearn.linear_model.SGDOneClassSVM can be used to approximate the solution of a kernelized One-Class SVM, implemented in sklearn.svm.OneClassSVM, with a linear complexity in the number of samples. Note that the complexity of a kernelized One-Class SVM is at best quadratic in the number of samples. sklearn.linear_model.SGDOneClassSVM is thus well suited for datasets with a large number of training samples (> 10,000) for which the SGD variant can be several orders of magnitude faster.

Mathematical details#

Its implementation is based on the implementation of the stochastic gradient descent. Indeed, the original optimization problem of the One-Class SVM is given by

\[\begin{split}\begin{aligned} \min_{w, \rho, \xi} & \quad \frac{1}{2}\Vert w \Vert^2 - \rho + \frac{1}{\nu n} \sum_{i=1}^n \xi_i \\ \text{s.t.} & \quad \langle w, x_i \rangle \geq \rho - \xi_i \quad 1 \leq i \leq n \\ & \quad \xi_i \geq 0 \quad 1 \leq i \leq n \end{aligned}\end{split}\]

where \(\nu \in (0, 1]\) is the user-specified parameter controlling the proportion of outliers and the proportion of support vectors. Getting rid of the slack variables \(\xi_i\) this problem is equivalent to

\[\min_{w, \rho} \frac{1}{2}\Vert w \Vert^2 - \rho + \frac{1}{\nu n} \sum_{i=1}^n \max(0, \rho - \langle w, x_i \rangle) \, .\]

Multiplying by the constant \(\nu\) and introducing the intercept \(b = 1 - \rho\) we obtain the following equivalent optimization problem

\[\min_{w, b} \frac{\nu}{2}\Vert w \Vert^2 + b\nu + \frac{1}{n} \sum_{i=1}^n \max(0, 1 - (\langle w, x_i \rangle + b)) \, .\]

This is similar to the optimization problems studied in section Mathematical formulation with \(y_i = 1, 1 \leq i \leq n\) and \(\alpha = \nu/2\), \(L\) being the hinge loss function and \(R\) being the L2 norm. We just need to add the term \(b\nu\) in the optimization loop.

As SGDClassifier and SGDRegressor, SGDOneClassSVM supports averaged SGD. Averaging can be enabled by setting average=True.

Examples

1.5.4. Stochastic Gradient Descent for sparse data#

Note

The sparse implementation produces slightly different results from the dense implementation, due to a shrunk learning rate for the intercept. See Implementation details.

There is built-in support for sparse data given in any matrix in a format supported by scipy.sparse. For maximum efficiency, however, use the CSR matrix format as defined in scipy.sparse.csr_matrix.

Examples

1.5.5. Complexity#

The major advantage of SGD is its efficiency, which is basically linear in the number of training examples. If X is a matrix of size (n, p) training has a cost of \(O(k n \bar p)\), where k is the number of iterations (epochs) and \(\bar p\) is the average number of non-zero attributes per sample.

Recent theoretical results, however, show that the runtime to get some desired optimization accuracy does not increase as the training set size increases.

1.5.6. Stopping criterion#

The classes SGDClassifier and SGDRegressor provide two criteria to stop the algorithm when a given level of convergence is reached:

  • With early_stopping=True, the input data is split into a training set and a validation set. The model is then fitted on the training set, and the stopping criterion is based on the prediction score (using the score method) computed on the validation set. The size of the validation set can be changed with the parameter validation_fraction.

  • With early_stopping=False, the model is fitted on the entire input data and the stopping criterion is based on the objective function computed on the training data.

In both cases, the criterion is evaluated once by epoch, and the algorithm stops when the criterion does not improve n_iter_no_change times in a row. The improvement is evaluated with absolute tolerance tol, and the algorithm stops in any case after a maximum number of iteration max_iter.

See Early stopping of Stochastic Gradient Descent for an example of the effects of early stopping.

1.5.7. Tips on Practical Use#

  • Stochastic Gradient Descent is sensitive to feature scaling, so it is highly recommended to scale your data. For example, scale each attribute on the input vector X to [0,1] or [-1,+1], or standardize it to have mean 0 and variance 1. Note that the same scaling must be applied to the test vector to obtain meaningful results. This can be easily done using StandardScaler:

    from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)  # Don't cheat - fit only on training data
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)  # apply same transformation to test data

# Or better yet: use a pipeline!
from sklearn.pipeline import make_pipeline
est = make_pipeline(StandardScaler(), SGDClassifier())
est.fit(X_train)
est.predict(X_test)

    If your attributes have an intrinsic scale (e.g. word frequencies or indicator features) scaling is not needed.

  • Finding a reasonable regularization term \(\alpha\) is best done using automatic hyper-parameter search, e.g. GridSearchCV or RandomizedSearchCV, usually in the range 10.0**-np.arange(1,7).

  • Empirically, we found that SGD converges after observing approximately 10^6 training samples. Thus, a reasonable first guess for the number of iterations is max_iter = np.ceil(10**6 / n), where n is the size of the training set.

  • If you apply SGD to features extracted using PCA we found that it is often wise to scale the feature values by some constant c such that the average L2 norm of the training data equals one.

  • We found that Averaged SGD works best with a larger number of features and a higher eta0.

References

1.5.8. Mathematical formulation#

We describe here the mathematical details of the SGD procedure. A good overview with convergence rates can be found in [12].

Given a set of training examples \((x_1, y_1), \ldots, (x_n, y_n)\) where \(x_i \in \mathbf{R}^m\) and \(y_i \in \mathbf{R}\) (\(y_i \in {-1, 1}\) for classification), our goal is to learn a linear scoring function \(f(x) = w^T x + b\) with model parameters \(w \in \mathbf{R}^m\) and intercept \(b \in \mathbf{R}\). In order to make predictions for binary classification, we simply look at the sign of \(f(x)\). To find the model parameters, we minimize the regularized training error given by

\[E(w,b) = \frac{1}{n}\sum_{i=1}^{n} L(y_i, f(x_i)) + \alpha R(w)\]

where \(L\) is a loss function that measures model (mis)fit and \(R\) is a regularization term (aka penalty) that penalizes model complexity; \(\alpha > 0\) is a non-negative hyperparameter that controls the regularization strength.

Loss functions details#

Different choices for \(L\) entail different classifiers or regressors:

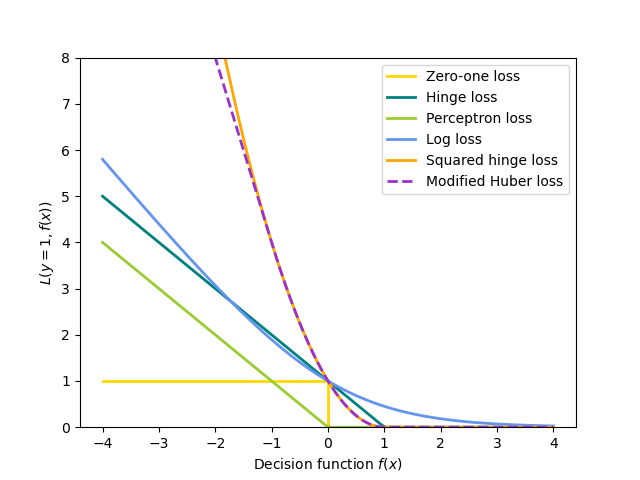
  • Hinge (soft-margin): equivalent to Support Vector Classification. \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))\).

  • Perceptron: \(L(y_i, f(x_i)) = \max(0, - y_i f(x_i))\).

  • Modified Huber: \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))^2\) if \(y_i f(x_i) > -1\), and \(L(y_i, f(x_i)) = -4 y_i f(x_i)\) otherwise.

  • Log Loss: equivalent to Logistic Regression. \(L(y_i, f(x_i)) = \log(1 + \exp (-y_i f(x_i)))\).

  • Squared Error: Linear regression (Ridge or Lasso depending on \(R\)). \(L(y_i, f(x_i)) = \frac{1}{2}(y_i - f(x_i))^2\).

  • Huber: less sensitive to outliers than least-squares. It is equivalent to least squares when \(|y_i - f(x_i)| \leq \varepsilon\), and \(L(y_i, f(x_i)) = \varepsilon |y_i - f(x_i)| - \frac{1}{2} \varepsilon^2\) otherwise.

  • Epsilon-Insensitive: (soft-margin) equivalent to Support Vector Regression. \(L(y_i, f(x_i)) = \max(0, |y_i - f(x_i)| - \varepsilon)\).

All of the above loss functions can be regarded as an upper bound on the misclassification error (Zero-one loss) as shown in the Figure below.

../_images/sphx_glr_plot_sgd_loss_functions_001.png

Popular choices for the regularization term \(R\) (the penalty parameter) include:

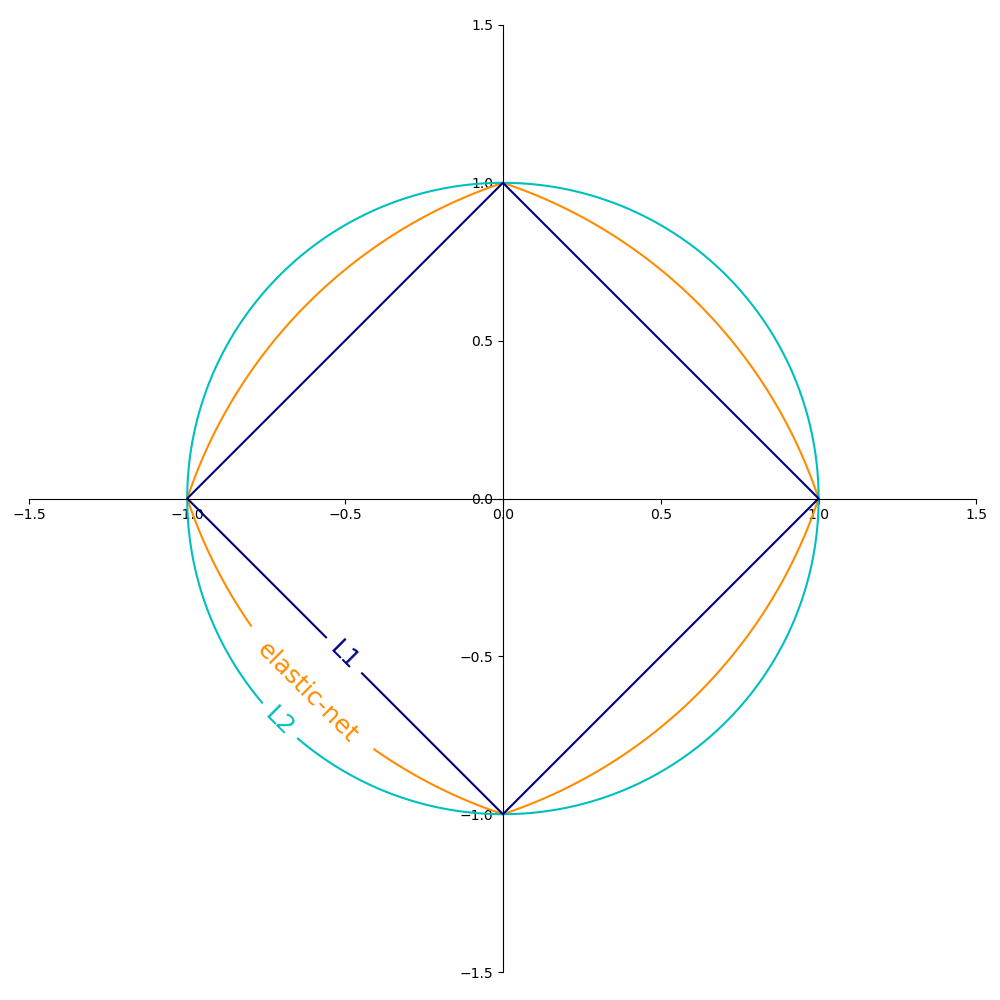
  • L2 norm: \(R(w) := \frac{1}{2} \sum_{j=1}^{m} w_j^2 = ||w||_2^2\),

  • L1 norm: \(R(w) := \sum_{j=1}^{m} |w_j|\), which leads to sparse solutions.

  • Elastic Net: \(R(w) := \frac{\rho}{2} \sum_{j=1}^{n} w_j^2 + (1-\rho) \sum_{j=1}^{m} |w_j|\), a convex combination of L2 and L1, where \(\rho\) is given by 1 - l1_ratio.

The Figure below shows the contours of the different regularization terms in a 2-dimensional parameter space (\(m=2\)) when \(R(w) = 1\).

../_images/sphx_glr_plot_sgd_penalties_001.png

1.5.8.1. SGD#

Stochastic gradient descent is an optimization method for unconstrained optimization problems. In contrast to (batch) gradient descent, SGD approximates the true gradient of \(E(w,b)\) by considering a single training example at a time.

The class SGDClassifier implements a first-order SGD learning routine. The algorithm iterates over the training examples and for each example updates the model parameters according to the update rule given by

\[w \leftarrow w - \eta \left[\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial L(w^T x_i + b, y_i)}{\partial w}\right]\]

where \(\eta\) is the learning rate which controls the step-size in the parameter space. The intercept \(b\) is updated similarly but without regularization (and with additional decay for sparse matrices, as detailed in Implementation details).

The learning rate \(\eta\) can be either constant or gradually decaying. For classification, the default learning rate schedule (learning_rate='optimal') is given by

\[\eta^{(t)} = \frac {1}{\alpha (t_0 + t)}\]

where \(t\) is the time step (there are a total of n_samples * n_iter time steps), \(t_0\) is determined based on a heuristic proposed by Léon Bottou such that the expected initial updates are comparable with the expected size of the weights (this assuming that the norm of the training samples is approx. 1). The exact definition can be found in _init_t in BaseSGD.

For regression the default learning rate schedule is inverse scaling (learning_rate='invscaling'), given by

\[\eta^{(t)} = \frac{eta_0}{t^{power\_t}}\]

where \(eta_0\) and \(power\_t\) are hyperparameters chosen by the user via eta0 and power_t, resp.

For a constant learning rate use learning_rate='constant' and use eta0 to specify the learning rate.

For an adaptively decreasing learning rate, use learning_rate='adaptive' and use eta0 to specify the starting learning rate. When the stopping criterion is reached, the learning rate is divided by 5, and the algorithm does not stop. The algorithm stops when the learning rate goes below 1e-6.

The model parameters can be accessed through the coef_ and intercept_ attributes: coef_ holds the weights \(w\) and intercept_ holds \(b\).

When using Averaged SGD (with the average parameter), coef_ is set to the average weight across all updates: coef_ \(= \frac{1}{T} \sum_{t=0}^{T-1} w^{(t)}\), where \(T\) is the total number of updates, found in the t_ attribute.

1.5.9. Implementation details#

The implementation of SGD is influenced by the Stochastic Gradient SVM of [7]. Similar to SvmSGD, the weight vector is represented as the product of a scalar and a vector which allows an efficient weight update in the case of L2 regularization. In the case of sparse input X, the intercept is updated with a smaller learning rate (multiplied by 0.01) to account for the fact that it is updated more frequently. Training examples are picked up sequentially and the learning rate is lowered after each observed example. We adopted the learning rate schedule from [8]. For multi-class classification, a “one versus all” approach is used. We use the truncated gradient algorithm proposed in [9] for L1 regularization (and the Elastic Net). The code is written in Cython.

References