1.3. Kernel ridge regression#
Kernel ridge regression (KRR) [M2012] combines Ridge regression and classification (linear least squares with \(L_2\)-norm regularization) with the kernel trick. It thus learns a linear function in the space induced by the respective kernel and the data. For non-linear kernels, this corresponds to a non-linear function in the original space.
The form of the model learned by KernelRidge is identical to support
vector regression (SVR). However, different loss
functions are used: KRR uses squared error loss while support vector
regression uses \(\epsilon\)-insensitive loss, both combined with \(L_2\)
regularization. In contrast to SVR, fitting
KernelRidge can be done in closed-form and is typically faster for
medium-sized datasets. On the other hand, the learned model is non-sparse and
thus slower than SVR, which learns a sparse model for
\(\epsilon > 0\), at prediction-time.
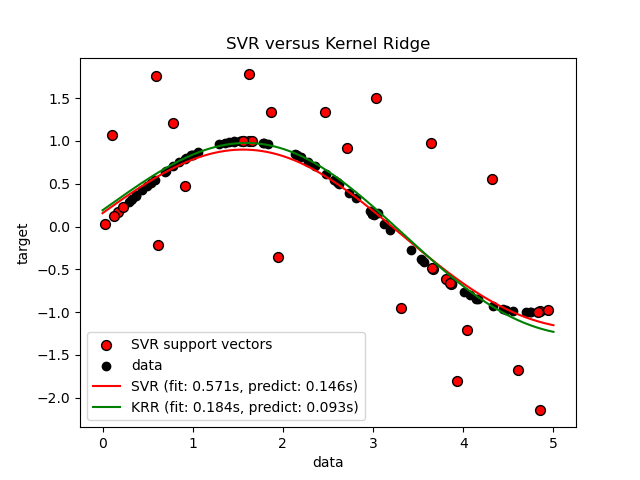
The following figure compares KernelRidge and
SVR on an artificial dataset, which consists of a
sinusoidal target function and strong noise added to every fifth datapoint.
The learned model of KernelRidge and SVR is
plotted, where both complexity/regularization and bandwidth of the RBF kernel
have been optimized using grid-search. The learned functions are very
similar; however, fitting KernelRidge is approximately seven times
faster than fitting SVR (both with grid-search).
However, prediction of 100,000 target values is more than three times faster
with SVR since it has learned a sparse model using only
approximately 1/3 of the 100 training datapoints as support vectors.
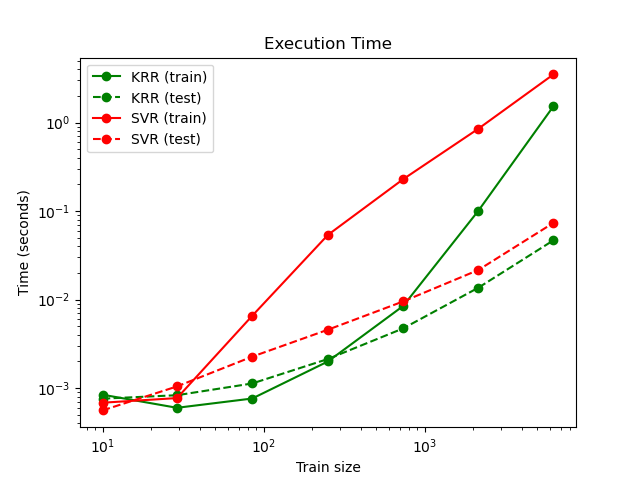
The next figure compares the time for fitting and prediction of
KernelRidge and SVR for different sizes of the
training set. Fitting KernelRidge is faster than
SVR for medium-sized training sets (less than 1000
samples); however, for larger training sets SVR scales
better. With regard to prediction time, SVR is faster
than KernelRidge for all sizes of the training set because of the
learned sparse solution. Note that the degree of sparsity and thus the
prediction time depends on the parameters \(\epsilon\) and \(C\) of
the SVR; \(\epsilon = 0\) would correspond to a
dense model.
Examples
References
“Machine Learning: A Probabilistic Perspective” Murphy, K. P. - chapter 14.4.3, pp. 492-493, The MIT Press, 2012