Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder
Ability of Gaussian process regression (GPR) to estimate data noise-level¶
This example shows the ability of the
WhiteKernel to estimate the noise
level in the data. Moreover, we show the importance of kernel hyperparameters
initialization.
# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
# Guillaume Lemaitre <guillaume.lemaitre@inria.fr>
# License: BSD 3 clause
Data generation¶
We will work in a setting where X will contain a single feature. We create a
function that will generate the target to be predicted. We will add an
option to add some noise to the generated target.
import numpy as np
def target_generator(X, add_noise=False):
target = 0.5 + np.sin(3 * X)
if add_noise:
rng = np.random.RandomState(1)
target += rng.normal(0, 0.3, size=target.shape)
return target.squeeze()
Let’s have a look to the target generator where we will not add any noise to observe the signal that we would like to predict.
X = np.linspace(0, 5, num=30).reshape(-1, 1)
y = target_generator(X, add_noise=False)
import matplotlib.pyplot as plt
plt.plot(X, y, label="Expected signal")
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")
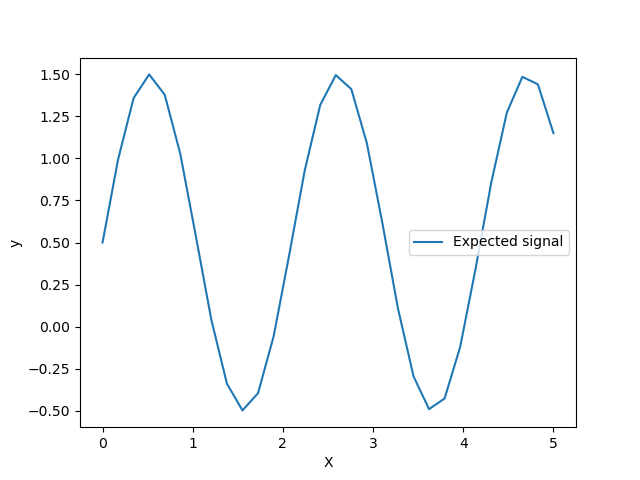
The target is transforming the input X using a sine function. Now, we will
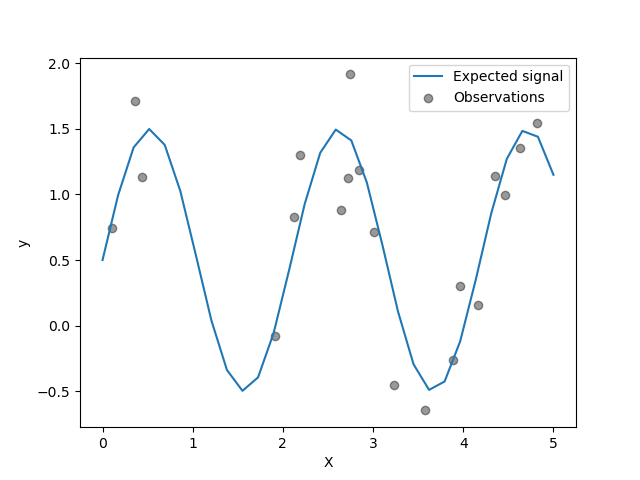
generate few noisy training samples. To illustrate the noise level, we will
plot the true signal together with the noisy training samples.
rng = np.random.RandomState(0)
X_train = rng.uniform(0, 5, size=20).reshape(-1, 1)
y_train = target_generator(X_train, add_noise=True)
plt.plot(X, y, label="Expected signal")
plt.scatter(
x=X_train[:, 0],
y=y_train,
color="black",
alpha=0.4,
label="Observations",
)
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")
Optimisation of kernel hyperparameters in GPR¶
Now, we will create a
GaussianProcessRegressor
using an additive kernel adding a
RBF and
WhiteKernel kernels.
The WhiteKernel is a kernel that
will able to estimate the amount of noise present in the data while the
RBF will serve at fitting the
non-linearity between the data and the target.
However, we will show that the hyperparameter space contains several local minima. It will highlights the importance of initial hyperparameter values.
We will create a model using a kernel with a high noise level and a large length scale, which will explain all variations in the data by noise.
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
kernel = 1.0 * RBF(length_scale=1e1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
noise_level=1, noise_level_bounds=(1e-5, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)
/home/circleci/project/sklearn/gaussian_process/kernels.py:455: ConvergenceWarning:
The optimal value found for dimension 0 of parameter k1__k2__length_scale is close to the specified upper bound 1000.0. Increasing the bound and calling fit again may find a better value.
plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std)
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
(
f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
),
fontsize=8,
)
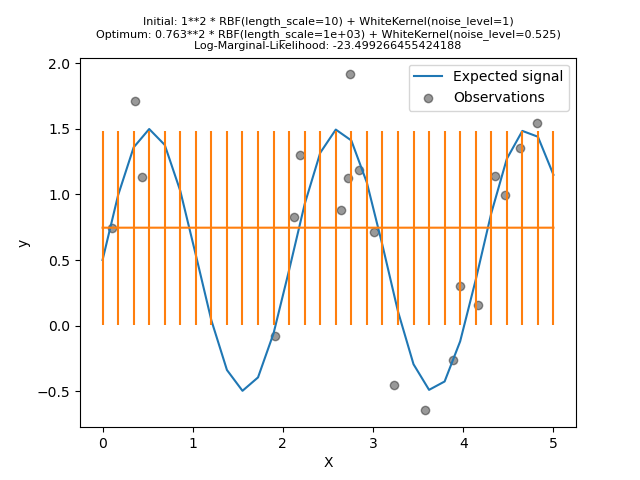
We see that the optimum kernel found still have a high noise level and an even larger length scale. Furthermore, we observe that the model does not provide faithful predictions.
Now, we will initialize the
RBF with a
larger length_scale and the
WhiteKernel
with a smaller noise level lower bound.
kernel = 1.0 * RBF(length_scale=1e-1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
noise_level=1e-2, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)
plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std)
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
(
f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
),
fontsize=8,
)
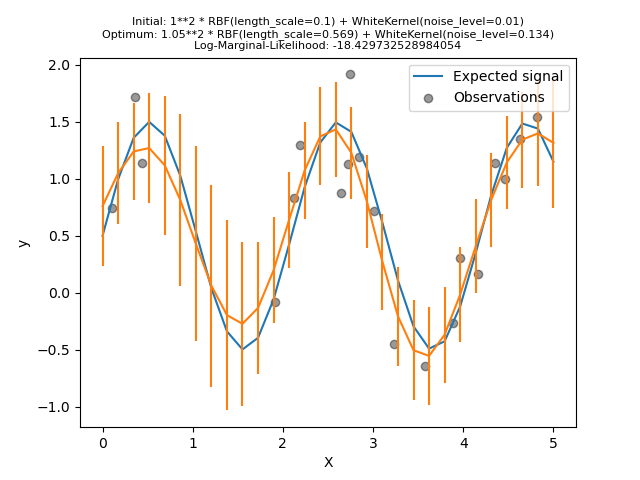
First, we see that the model’s predictions are more precise than the previous model’s: this new model is able to estimate the noise-free functional relationship.
Looking at the kernel hyperparameters, we see that the best combination found has a smaller noise level and shorter length scale than the first model.
We can inspect the Log-Marginal-Likelihood (LML) of
GaussianProcessRegressor
for different hyperparameters to get a sense of the local minima.
from matplotlib.colors import LogNorm
length_scale = np.logspace(-2, 4, num=50)
noise_level = np.logspace(-2, 1, num=50)
length_scale_grid, noise_level_grid = np.meshgrid(length_scale, noise_level)
log_marginal_likelihood = [
gpr.log_marginal_likelihood(theta=np.log([0.36, scale, noise]))
for scale, noise in zip(length_scale_grid.ravel(), noise_level_grid.ravel())
]
log_marginal_likelihood = np.reshape(
log_marginal_likelihood, newshape=noise_level_grid.shape
)
vmin, vmax = (-log_marginal_likelihood).min(), 50
level = np.around(np.logspace(np.log10(vmin), np.log10(vmax), num=50), decimals=1)
plt.contour(
length_scale_grid,
noise_level_grid,
-log_marginal_likelihood,
levels=level,
norm=LogNorm(vmin=vmin, vmax=vmax),
)
plt.colorbar()
plt.xscale("log")
plt.yscale("log")
plt.xlabel("Length-scale")
plt.ylabel("Noise-level")
plt.title("Log-marginal-likelihood")
plt.show()
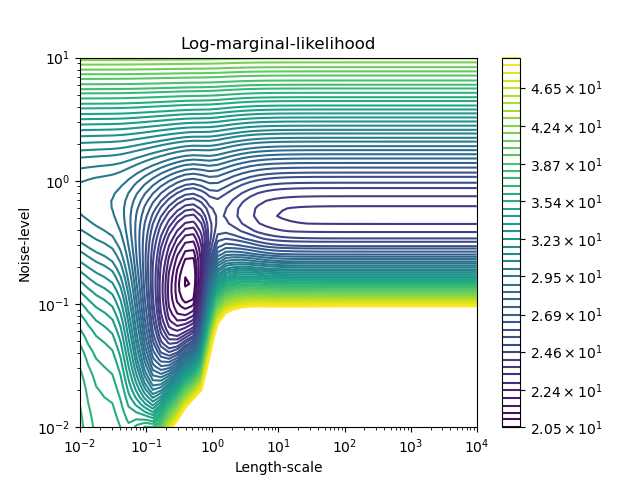
We see that there are two local minima that correspond to the combination of hyperparameters previously found. Depending on the initial values for the hyperparameters, the gradient-based optimization might converge whether or not to the best model. It is thus important to repeat the optimization several times for different initializations.
Total running time of the script: (0 minutes 2.641 seconds)
Related examples
Illustration of prior and posterior Gaussian process for different kernels
Gaussian Processes regression: basic introductory example
Forecasting of CO2 level on Mona Loa dataset using Gaussian process regression (GPR)
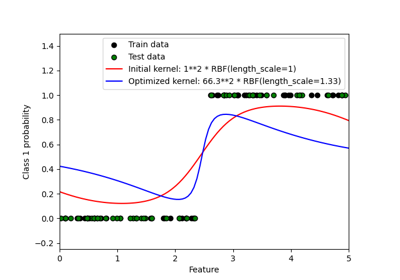
Probabilistic predictions with Gaussian process classification (GPC)
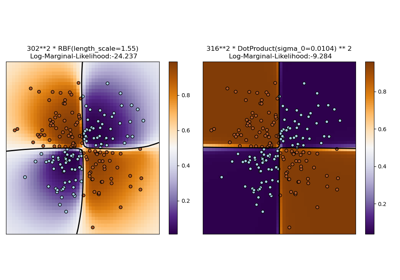
Illustration of Gaussian process classification (GPC) on the XOR dataset