Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder
Probability Calibration curves¶
When performing classification one often wants to predict not only the class label, but also the associated probability. This probability gives some kind of confidence on the prediction. This example demonstrates how to visualize how well calibrated the predicted probabilities are using calibration curves, also known as reliability diagrams. Calibration of an uncalibrated classifier will also be demonstrated.
# Author: Alexandre Gramfort <alexandre.gramfort@telecom-paristech.fr>
# Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
# License: BSD 3 clause.
Dataset¶
We will use a synthetic binary classification dataset with 100,000 samples and 20 features. Of the 20 features, only 2 are informative, 10 are redundant (random combinations of the informative features) and the remaining 8 are uninformative (random numbers). Of the 100,000 samples, 1,000 will be used for model fitting and the rest for testing.
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
X, y = make_classification(
n_samples=100_000, n_features=20, n_informative=2, n_redundant=10, random_state=42
)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.99, random_state=42
)
Calibration curves¶
Gaussian Naive Bayes¶
First, we will compare:
LogisticRegression(used as baseline since very often, properly regularized logistic regression is well calibrated by default thanks to the use of the log-loss)Uncalibrated
GaussianNBGaussianNBwith isotonic and sigmoid calibration (see User Guide)
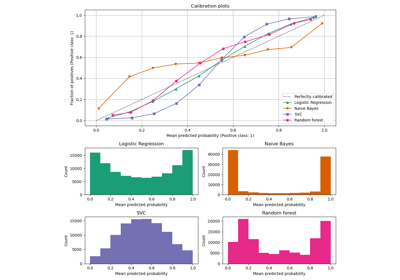
Calibration curves for all 4 conditions are plotted below, with the average predicted probability for each bin on the x-axis and the fraction of positive classes in each bin on the y-axis.
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from sklearn.calibration import CalibratedClassifierCV, CalibrationDisplay
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
lr = LogisticRegression(C=1.0)
gnb = GaussianNB()
gnb_isotonic = CalibratedClassifierCV(gnb, cv=2, method="isotonic")
gnb_sigmoid = CalibratedClassifierCV(gnb, cv=2, method="sigmoid")
clf_list = [
(lr, "Logistic"),
(gnb, "Naive Bayes"),
(gnb_isotonic, "Naive Bayes + Isotonic"),
(gnb_sigmoid, "Naive Bayes + Sigmoid"),
]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
colors = plt.get_cmap("Dark2")
ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
display = CalibrationDisplay.from_estimator(
clf,
X_test,
y_test,
n_bins=10,
name=name,
ax=ax_calibration_curve,
color=colors(i),
)
calibration_displays[name] = display
ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (Naive Bayes)")
# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
row, col = grid_positions[i]
ax = fig.add_subplot(gs[row, col])
ax.hist(
calibration_displays[name].y_prob,
range=(0, 1),
bins=10,
label=name,
color=colors(i),
)
ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")
plt.tight_layout()
plt.show()
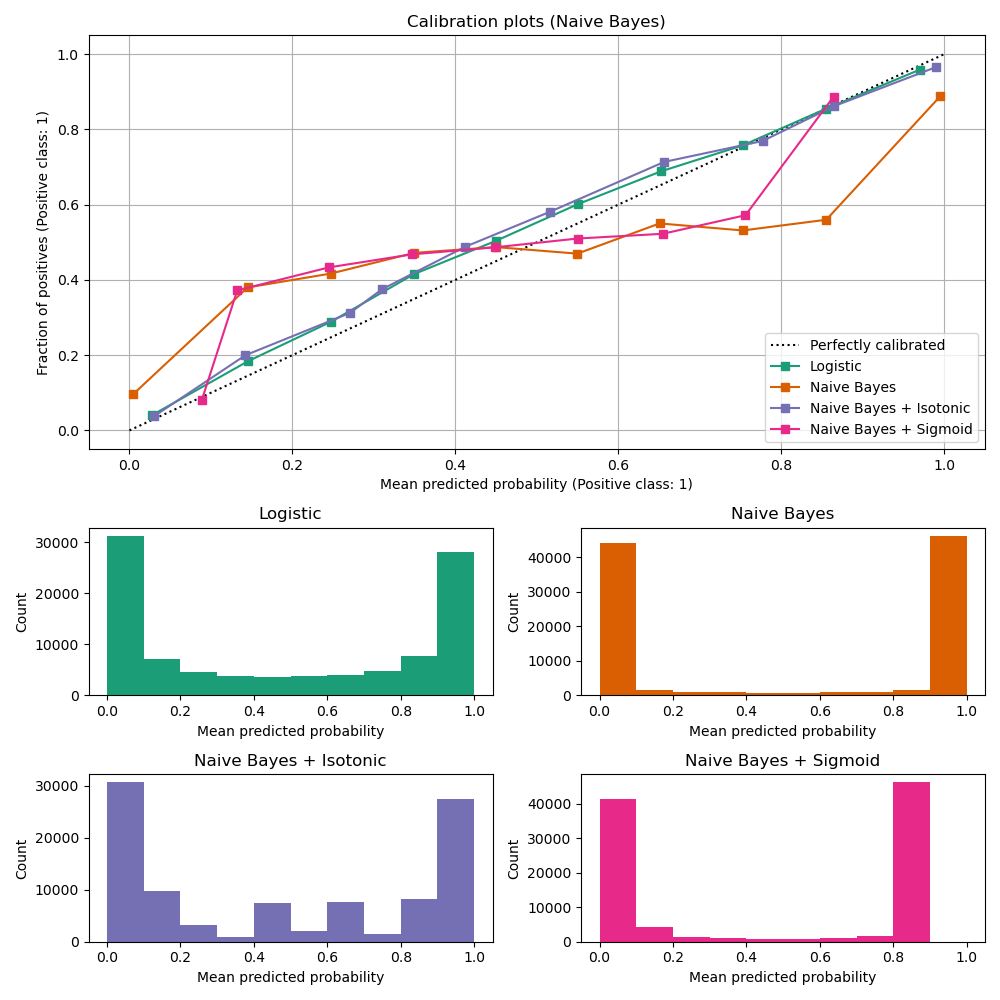
Uncalibrated GaussianNB is poorly calibrated
because of
the redundant features which violate the assumption of feature-independence
and result in an overly confident classifier, which is indicated by the
typical transposed-sigmoid curve. Calibration of the probabilities of
GaussianNB with Isotonic regression can fix
this issue as can be seen from the nearly diagonal calibration curve.
Sigmoid regression also improves calibration
slightly,
albeit not as strongly as the non-parametric isotonic regression. This can be
attributed to the fact that we have plenty of calibration data such that the
greater flexibility of the non-parametric model can be exploited.
Below we will make a quantitative analysis considering several classification metrics: Brier score loss, Log loss, precision, recall, F1 score and ROC AUC.
from collections import defaultdict
import pandas as pd
from sklearn.metrics import (
brier_score_loss,
f1_score,
log_loss,
precision_score,
recall_score,
roc_auc_score,
)
scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
y_prob = clf.predict_proba(X_test)
y_pred = clf.predict(X_test)
scores["Classifier"].append(name)
for metric in [brier_score_loss, log_loss, roc_auc_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_prob[:, 1]))
for metric in [precision_score, recall_score, f1_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_pred))
score_df = pd.DataFrame(scores).set_index("Classifier")
score_df.round(decimals=3)
score_df
Notice that although calibration improves the Brier score loss (a metric composed of calibration term and refinement term) and Log loss, it does not significantly alter the prediction accuracy measures (precision, recall and F1 score). This is because calibration should not significantly change prediction probabilities at the location of the decision threshold (at x = 0.5 on the graph). Calibration should however, make the predicted probabilities more accurate and thus more useful for making allocation decisions under uncertainty. Further, ROC AUC, should not change at all because calibration is a monotonic transformation. Indeed, no rank metrics are affected by calibration.
Linear support vector classifier¶
Next, we will compare:
LogisticRegression(baseline)Uncalibrated
LinearSVC. Since SVC does not output probabilities by default, we naively scale the output of the decision_function into [0, 1] by applying min-max scaling.LinearSVCwith isotonic and sigmoid calibration (see User Guide)
import numpy as np
from sklearn.svm import LinearSVC
class NaivelyCalibratedLinearSVC(LinearSVC):
"""LinearSVC with `predict_proba` method that naively scales
`decision_function` output for binary classification."""
def fit(self, X, y):
super().fit(X, y)
df = self.decision_function(X)
self.df_min_ = df.min()
self.df_max_ = df.max()
def predict_proba(self, X):
"""Min-max scale output of `decision_function` to [0, 1]."""
df = self.decision_function(X)
calibrated_df = (df - self.df_min_) / (self.df_max_ - self.df_min_)
proba_pos_class = np.clip(calibrated_df, 0, 1)
proba_neg_class = 1 - proba_pos_class
proba = np.c_[proba_neg_class, proba_pos_class]
return proba
lr = LogisticRegression(C=1.0)
svc = NaivelyCalibratedLinearSVC(max_iter=10_000, dual="auto")
svc_isotonic = CalibratedClassifierCV(svc, cv=2, method="isotonic")
svc_sigmoid = CalibratedClassifierCV(svc, cv=2, method="sigmoid")
clf_list = [
(lr, "Logistic"),
(svc, "SVC"),
(svc_isotonic, "SVC + Isotonic"),
(svc_sigmoid, "SVC + Sigmoid"),
]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
display = CalibrationDisplay.from_estimator(
clf,
X_test,
y_test,
n_bins=10,
name=name,
ax=ax_calibration_curve,
color=colors(i),
)
calibration_displays[name] = display
ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (SVC)")
# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
row, col = grid_positions[i]
ax = fig.add_subplot(gs[row, col])
ax.hist(
calibration_displays[name].y_prob,
range=(0, 1),
bins=10,
label=name,
color=colors(i),
)
ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")
plt.tight_layout()
plt.show()
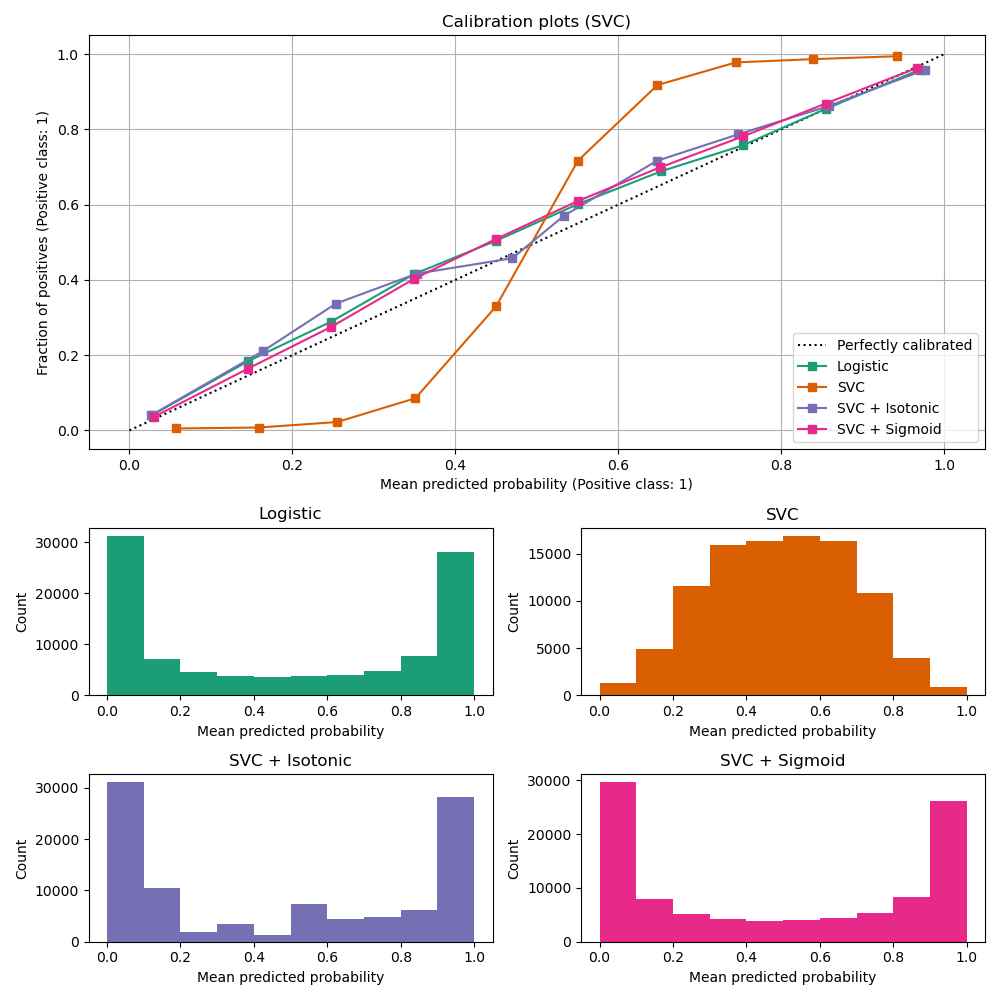
LinearSVC shows the opposite
behavior to GaussianNB; the calibration
curve has a sigmoid shape, which is typical for an under-confident
classifier. In the case of LinearSVC, this is caused
by the margin property of the hinge loss, which focuses on samples that are
close to the decision boundary (support vectors). Samples that are far
away from the decision boundary do not impact the hinge loss. It thus makes
sense that LinearSVC does not try to separate samples
in the high confidence region regions. This leads to flatter calibration
curves near 0 and 1 and is empirically shown with a variety of datasets
in Niculescu-Mizil & Caruana [1].
Both kinds of calibration (sigmoid and isotonic) can fix this issue and yield similar results.
As before, we show the Brier score loss, Log loss, precision, recall, F1 score and ROC AUC.
scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
y_prob = clf.predict_proba(X_test)
y_pred = clf.predict(X_test)
scores["Classifier"].append(name)
for metric in [brier_score_loss, log_loss, roc_auc_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_prob[:, 1]))
for metric in [precision_score, recall_score, f1_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_pred))
score_df = pd.DataFrame(scores).set_index("Classifier")
score_df.round(decimals=3)
score_df
As with GaussianNB above, calibration improves
both Brier score loss and Log loss but does not alter the
prediction accuracy measures (precision, recall and F1 score) much.
Summary¶
Parametric sigmoid calibration can deal with situations where the calibration
curve of the base classifier is sigmoid (e.g., for
LinearSVC) but not where it is transposed-sigmoid
(e.g., GaussianNB). Non-parametric
isotonic calibration can deal with both situations but may require more
data to produce good results.
References¶
Total running time of the script: (0 minutes 2.269 seconds)
Related examples
Probability Calibration for 3-class classification