adjusted_mutual_info_score#
- sklearn.metrics.adjusted_mutual_info_score(labels_true, labels_pred, *, average_method='arithmetic')[source]#
Adjusted Mutual Information between two clusterings.
Adjusted Mutual Information (AMI) is an adjustment of the Mutual Information (MI) score to account for chance. It accounts for the fact that the MI is generally higher for two clusterings with a larger number of clusters, regardless of whether there is actually more information shared. For two clusterings \(U\) and \(V\), the AMI is given as:
AMI(U, V) = [MI(U, V) - E(MI(U, V))] / [avg(H(U), H(V)) - E(MI(U, V))]
This metric is independent of the absolute values of the labels: a permutation of the class or cluster label values won’t change the score value in any way.
This metric is furthermore symmetric: switching \(U\) (
label_true) with \(V\) (labels_pred) will return the same score value. This can be useful to measure the agreement of two independent label assignments strategies on the same dataset when the real ground truth is not known.Be mindful that this function is an order of magnitude slower than other metrics, such as the Adjusted Rand Index.
Read more in the User Guide.
- Parameters:
- labels_trueint array-like of shape (n_samples,)
A clustering of the data into disjoint subsets, called \(U\) in the above formula.
- labels_predint array-like of shape (n_samples,)
A clustering of the data into disjoint subsets, called \(V\) in the above formula.
- average_method{‘min’, ‘geometric’, ‘arithmetic’, ‘max’}, default=’arithmetic’
How to compute the normalizer in the denominator.
Added in version 0.20.
Changed in version 0.22: The default value of
average_methodchanged from ‘max’ to ‘arithmetic’.
- Returns:
- ami: float (upperlimited by 1.0)
The AMI returns a value of 1 when the two partitions are identical (ie perfectly matched). Random partitions (independent labellings) have an expected AMI around 0 on average hence can be negative. The value is in adjusted nats (based on the natural logarithm).
See also
adjusted_rand_scoreAdjusted Rand Index.
mutual_info_scoreMutual Information (not adjusted for chance).
References
Examples
Perfect labelings are both homogeneous and complete, hence have score 1.0:
>>> from sklearn.metrics.cluster import adjusted_mutual_info_score >>> adjusted_mutual_info_score([0, 0, 1, 1], [0, 0, 1, 1]) ... 1.0 >>> adjusted_mutual_info_score([0, 0, 1, 1], [1, 1, 0, 0]) ... 1.0
If classes members are completely split across different clusters, the assignment is totally in-complete, hence the AMI is null:
>>> adjusted_mutual_info_score([0, 0, 0, 0], [0, 1, 2, 3]) ... 0.0
Gallery examples#
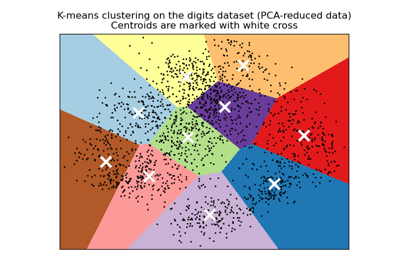
A demo of K-Means clustering on the handwritten digits data
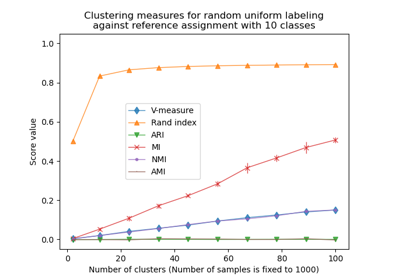
Adjustment for chance in clustering performance evaluation